ACM计划

原文 ：http://027xbc.blog.163.com/blog/static/128159658201141371343475/

ACM主要是考算法的,主要时间是花在思考算法上，不是花在写程序与debug上。

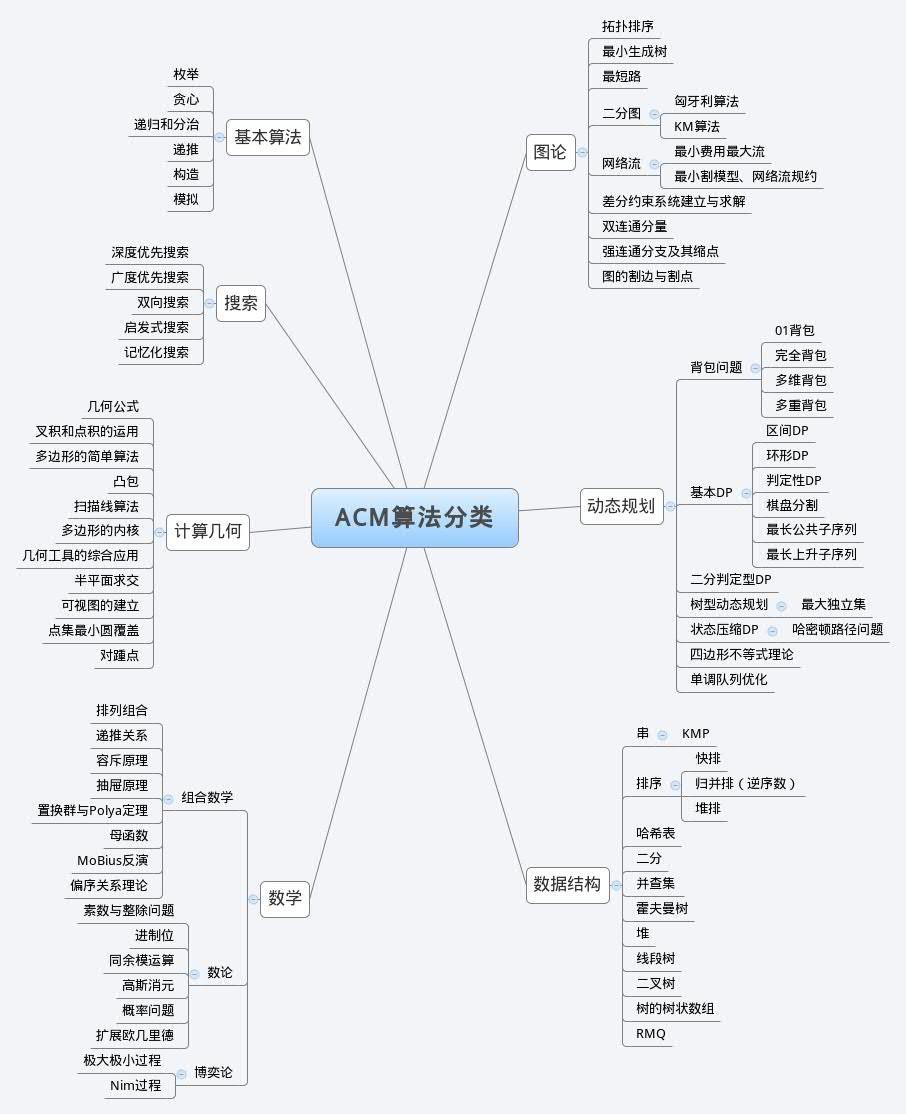
下面给个计划：

第一阶段：练经典常用算法，下面的每个算法给我打上十到二十遍，同时自己精简代码，
因为太常用，所以要练到写时不用想，10-15分钟内打完，甚至关掉显示器都可以把程序打
出来. 
1.最短路(Floyd、Dijstra,BellmanFord，spfa) 
2.最小生成树(先写个prim,kruscal要用并查集，不好写) 
3.大数（高精度）加减乘除 
4.二分查找. (代码可在五行以内) 
5.叉乘、判线段相交、然后写个凸包. 
6.BFS、DFS,同时熟练hash表(要熟，要灵活,代码要简) 
7.数学上的有：辗转相除（两行内），线段交点、多角形面积公式. 
8. 调用系统的qsort, 技巧很多，慢慢掌握. 
9. 任意进制间的转换

第二阶段：练习复杂一点，但也较常用的算法。 
如： 
1. 二分图匹配（匈牙利），最小路径覆盖 
2. 网络流，最小费用流。 
3. 线段树. 
4. 并查集。 
5. 熟悉动态规划的各个典型：LCS、最长递增子串、三角剖分、记忆化dp 
6.博弈类算法。博弈树，二进制法等。 
7.最大团，最大独立集。 
8.判断点在多边形内。 
9. 差分约束系统. 
10. 双向广度搜索、A*算法，最小耗散优先.

ACMer必备知识（这么多呀，慢慢学了……)

图论

路径问题
        0/1边权最短路径
        BFS
        非负边权最短路径（Dijkstra）
            可以用Dijkstra解决问题的特征
        负边权最短路径
        Bellman-Ford
            Bellman-Ford的Yen-氏优化
            差分约束系统
        Floyd
            广义路径问题
            传递闭包
            极小极大距离 / 极大极小距离
        Euler Path / Tour
            圈套圈算法
            混合图的 Euler Path / Tour
        Hamilton Path / Tour
            特殊图的Hamilton Path / Tour 构造
    生成树问题
        最小生成树
        第k小生成树
        最优比率生成树
        0/1分数规划
        度限制生成树
    连通性问题
        强大的DFS算法
        无向图连通性
            割点
            割边
            二连通分支
            有向图连通性
            强连通分支
            2-SAT
            最小点基
    有向无环图
        拓扑排序
            有向无环图与动态规划的关系
    二分图匹配问题
        一般图问题与二分图问题的转换思路
        最大匹配
            有向图的最小路径覆盖
            0 / 1矩阵的最小覆盖
        完备匹配
        最优匹配
        稳定婚姻
    网络流问题
        网络流模型的简单特征和与线性规划的关系
        最大流最小割定理
        最大流问题
            有上下界的最大流问题
                循环流
        最小费用最大流 / 最大费用最大流
    弦图的性质和判定

组合数学

解决组合数学问题时常用的思想
        逼近
        递推 / 动态规划
    概率问题
        Polya定理

计算几何 / 解析几何

计算几何的核心：叉积 / 面积
    解析几何的主力：复数
    基本形
        点
        直线，线段
        多边形
    凸多边形 / 凸包
        凸包算法的引进，卷包裹法
    Graham扫描法
        水平序的引进，共线凸包的补丁
    完美凸包算法
    相关判定
        两直线相交
        两线段相交
        点在任意多边形内的判定
        点在凸多边形内的判定
    经典问题
        最小外接圆
            近似O(n)的最小外接圆算法
        点集直径
            旋转卡壳，对踵点
        多边形的三角剖分

数学 / 数论

最大公约数
        Euclid算法
            扩展的Euclid算法
                同余方程 / 二元一次不定方程
                同余方程组
    线性方程组
        高斯消元法
            解mod 2域上的线性方程组
        整系数方程组的精确解法
    矩阵
        行列式的计算
            利用矩阵乘法快速计算递推关系
    分数
        分数树
        连分数逼近
    数论计算
        求N的约数个数
        求phi(N)
        求约数和
        快速数论变换
        ……
    素数问题
        概率判素算法
        概率因子分解

数据结构

组织结构
        二叉堆
        左偏树
        二项树
        胜者树
        跳跃表
        样式图标
        斜堆
        heap
    统计结构
        树状数组
        虚二叉树
        线段树
            矩形面积并
            圆形面积并
    关系结构
        Hash表
        并查集
            路径压缩思想的应用
    STL中的数据结构
        vector
        deque
        set / map

动态规划 / 记忆化搜索

动态规划和记忆化搜索在思考方式上的区别
    最长子序列系列问题
        最长不下降子序列
        最长公共子序列
        最长公共不下降子序列
    一类NP问题的动态规划解法
    树型动态规划
    背包问题
    动态规划的优化
        四边形不等式
        函数的凸凹性
        状态设计
        规划方向

线性规划

常用思想

    二分
    最小表示法

串

KMP
    Trie结构
    后缀树/后缀数组
    LCA/RMQ
    有限状态自动机理论

排序
    选择/冒泡
    快速排序
    堆排序
    归并排序
    基数排序
    拓扑排序
    排序网络