旋转卡壳（求凸包直径）学习笔记 | 题解 P1452 [USACO03FALL]Beauty Contest G /【模板】旋转卡壳

前言

旋转卡壳（Rotating Calipers）可以在凸包上维护许多有用的信息，最常见的就是凸包直径（平面最远点对）。

注意：本文不介绍所谓的 “人类智慧” 乱搞做法。

算法流程

首先我们需要求出点集的凸包（我个人喜欢 Andrew 算法）。

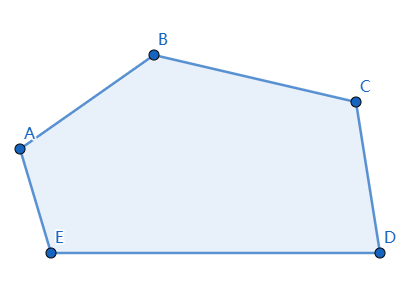
然后我们考虑选定凸包的一条边所在的直线，比如 \(AB\)。然后找到凸包的所有顶点中离它最远的点，在这个例子中是 \(D\)。然后凸包直径就 可能 是 \(AD\) 或 \(BD\)。

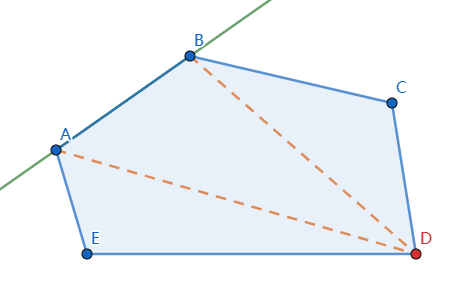
然后我们继续。逆时针选择下一条边 \(AE\)，这时我们发现最远点变成了 \(C\)，然后尝试用 \(AC,EC\) 更新答案。以此类推。这样我们就找到了凸包直径。

但是这样子时间复杂度是 \(O(n^2)\) 的，应该无法通过。

但是根据以前的经验，似乎最远点也是逆时针旋转的。换句话说，逆时针遍历的点到直线的距离单调。

这也可以用凸包的凸性来解释。我无法给出详细证明，但是大家不妨手动画几个图，就可以感性的理解了。

于是我们就可以用一个漂亮的双指针解决了。

P145 【模板】旋转卡壳 代码

注意本题需要输出凸包直径的平方。

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n;

const double eps=1e-9;
int dcmp(double x){
    return (fabs(x)<=eps)?0:(x<0?-1:1);
}
struct Point{
    double x,y;
    Point(double X=0,double Y=0){x=X,y=Y;}
};
struct Vector{
    double x,y;
    Vector(double X=0,double Y=0){x=X,y=Y;}
};
inline Vector operator-(Point x,Point y){// 点-点=向量
    return Vector(x.x-y.x,x.y-y.y);
}
inline double cross(Vector x,Vector y){ // 向量叉积
    return x.x*y.y-x.y*y.x;
}
inline double operator*(Vector x,Vector y){ // 向量叉积
    return cross(x,y);
}
inline double len(Vector x){ // 向量模长
    return sqrt(x.x*x.x+x.y*x.y);
}

int stk[50005];
bool used[50005];
vector<Point> ConvexHull(Point* poly, int n){ // Andrew算法求凸包
    int top=0;
    sort(poly+1,poly+n+1,[&](Point x,Point y){
        return (x.x==y.x)?(x.y<y.y):(x.x<y.x);
    });
    stk[++top]=1;
    for(int i=2;i<=n;i++){
        while(top>1&&dcmp((poly[stk[top]]-poly[stk[top-1]])*(poly[i]-poly[stk[top]]))<=0){
            used[stk[top--]]=0;
        }
        used[i]=1;
        stk[++top]=i;
    }
    int tmp=top;
    for(int i=n-1;i;i--){
        if(used[i]) continue;
        while(top>tmp&&dcmp((poly[stk[top]]-poly[stk[top-1]])*(poly[i]-poly[stk[top]]))<=0){
            used[stk[top--]]=0;
        }
        used[i]=1;
        stk[++top]=i;
    }
    vector<Point> a;
    for(int i=1;i<=top;i++){
        a.push_back(poly[stk[i]]);
    }
    return a;
}

struct Line{
    Point x;Vector y;
    Line(Point X,Vector Y){x=X,y=Y;}
    Line(Point X,Point Y){x=X,y=Y-X;}
};

inline double DistanceToLine(Point P,Line x){// 点到直线的距离
    Vector v1=x.y, v2=P-x.x;
    return fabs(cross(v1,v2))/len(v1);
}

double RoatingCalipers(vector<Point> poly){// 旋转卡壳
    if(poly.size()==3) return len(poly[1]-poly[0]);
    int cur=0;
    double ans=0;
    for(int i=0;i<poly.size()-1;i++){
        Line line(poly[i],poly[i+1]);
        while(DistanceToLine(poly[cur], line) <= DistanceToLine(poly[(cur+1)%poly.size()], line)){
            cur=(cur+1)%poly.size();
        }
        ans=max(ans, max(len(poly[i]-poly[cur]), len(poly[i+1]-poly[cur])));
    }
    return ans;
}

Point poly[50005];

signed main(){
    cin>>n;
    for(int i=1;i<=n;i++) cin>>poly[i].x>>poly[i].y;
    double v=RoatingCalipers(ConvexHull(poly, n));
    cout<<(int)(v*v);
    return 0;
}