【学习笔记】Tarjan 图论算法

- 前言

本文主要介绍 Tarjan 算法的「强连通分量」「割点」「桥」等算法。

争取写的好懂一些。

- 「强连通分量」

- 何为「强连通分量」

在有向图中，如果任意两个点都能通过直接或间接的路径相互通达，那么就称这个有向图是「强连通」的。

如果这个有向图的子图是「强连通」的，我们就称这个子图为「强连通分量」。

特别的，单独一个点也算是一个强连通分量。

例如下图 \(^{\texttt{[1]}}\)：

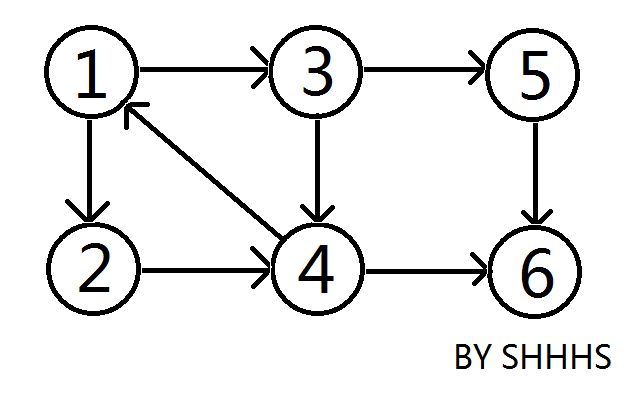
我们发现，\(\{1,3,2,4\}\) 这个子图无论从哪个节点出发，均能到达其他的节点，所以它是一个强连通分量。

同理 \(\{5\}\{6\}\) 单个节点独自构成一个强连通分量。

- Tarjan

我们对每个节点定义两个值：\(\text{dfn}_i\) 和 \(\text{low}_i\)。

• \(\text{dfn}_i\)：表示这个节点的 dfs 序，即它在 dfs 中是第几个被访问到的。
• \(\text{low}_i\)：表示这个节点能追溯到的在栈中节点的最早的已经在栈中的节点。

其中，以 \(u\) 为根的 dfs 树的 \(\text{dfn}\) 值严格大于 \(\text{dfn}_u\) 的值。

其中，每访问到一个节点时，我们初始化为 \(\text{dfn}_i=\text{low}_i=dfs\_num\)，其中 \(dfs\_num\) 是 dfs 序，每访问到一个点就使其的值增加 \(1\)，把它压入手工栈，并标明它在栈中。

然后我们接着访问它下面的一个节点：

1. 它没被访问过，不在栈中，就先 \(\text{dfs}(v)\)，对他进行深搜，并在回溯过程中以 \(\text{low}_v\) 更新 \(\text{low}_u\)（因为 \(v\) 可以访问到的节点 \(u\) 一定也可以访问到）。
2. 它被访问过，在栈中，根据 \(\text{low}\) 的定义，用 \(\text{dfn}_v\) 更新 \(\text{low}_u\)。\(^{\texttt{[2]}}\)
3. 它被访问过，不在栈中，这就说明它已经在一个强连通分量中了，无需更新。

---

接下来我们来看看当 \(\text{dfn}_i=\text{low}_i\) 的时候会发生什么。

根据定义，这个强联通分量中只有一个点的 \(\text{dfn}\) 值和 \(\text{low}\) 相等，就是 dfs 碰到的第一个强连通分量的点，它的 \(\text{low}\) 值不随其他点而影响。

因此，如果 \(\text{dfn}_i=\text{low}_i\)，那么它和它栈上方的点共同构成一个强连通分量。

总体的时间复杂度是 \(\Theta(V+E)\) 的，非常优秀。

- 图解

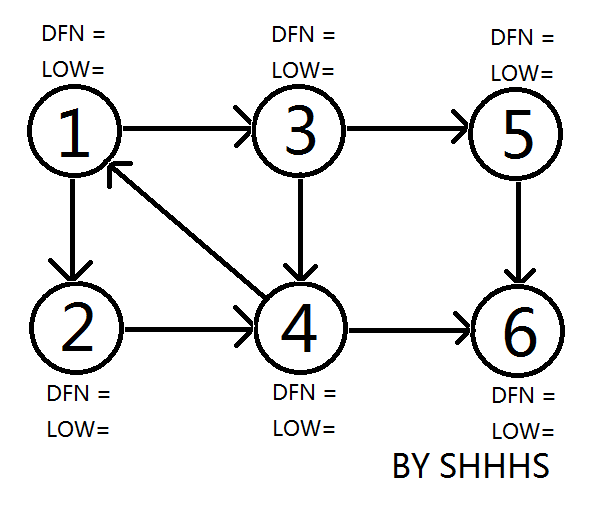
起始图，从 \(1\) 开始遍历。

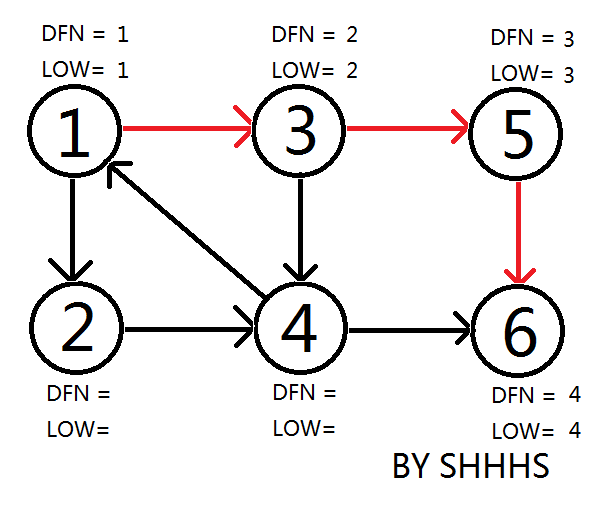
顺次搜到 \(3 \to 5 \to 6\)，更新 \(\text{dfn}\) 和 \(\text{low}\)，压进栈。

发现 \(6\) 没有可以拓展的点了。因为 \(\text{dfn}_6=\text{low}_6\)，所以它和它栈上面的点（即使他是栈顶）构成强连通分量。将 \(6\) 及 \(6\) 以上的点弹出。

回溯发现 \(5\) 没有可以拓展的点了。因为 \(\text{dfn}_5=\text{low}_5\)，所以它和它栈上面的点（即使他是栈顶）构成强连通分量。

至此找到两个强连通分量：\(\{5\}\{6\}\)。

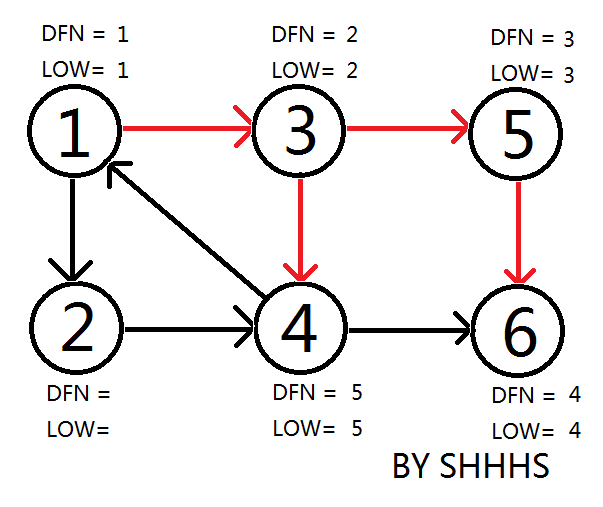
回溯时拓展 \(3\) 到 \(4\)，更新 \(\text{dfn}\) 和 \(\text{low}\)，压进栈。

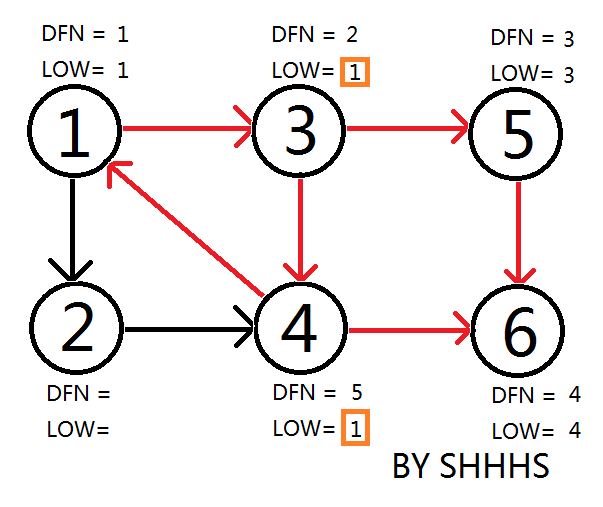
回到节点 \(1\)，因为它被搜索过且在栈中，更新 \(3\) 和 \(4\) 的 \(\text{low}\)。

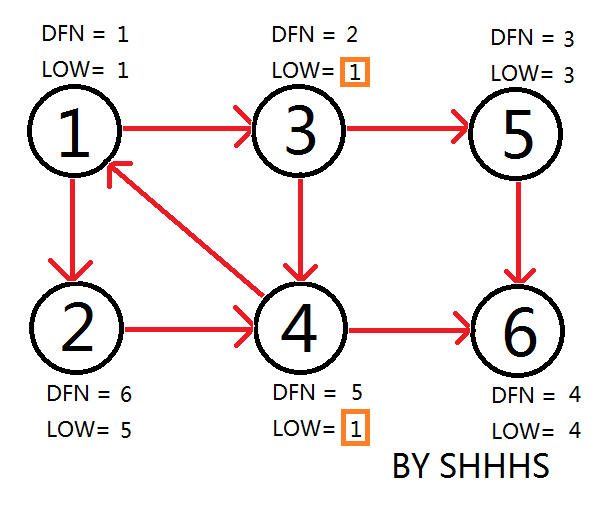
回溯 \(4 \to 3 \to 1\)，因为 \(1\) 还能拓展，继续到 \(2\)，\(2\) 到 \(4\)，更新 \(\text{low}\)。

虽然 \(2\) 没有可以拓展的点了，但是它的 \(\text{dfn}_i \neq \text{low}_i\)，回溯。

到 \(1\)，发现 \(\text{dfn}_i = \text{low}_i\)，弹出所有点为一个强连通分量。

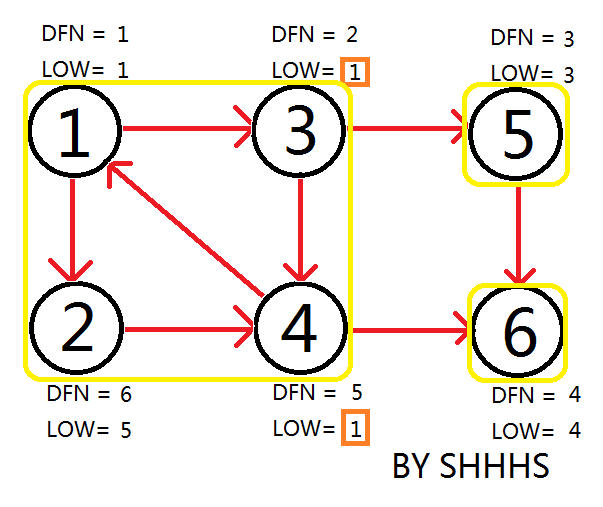
至此，Tarjan Algorithm 结束，强连通分量为 \(\{1,3,2,4\},\{5\},\{6\}\)。

- 代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 5;

int scc[N], stk[N], top, dfn[N], low[N], dfs_num, col_num;
bool vis[N];
vector<int> G[N];

void tarjan(int u){
	dfn[u] = low[u] = ++dfs_num;
	stk[++ top] = u; vis[u] = true;
	for(auto &v : G[u]){
		if(!dfn[v]){
			tarjan(v);
			low[u] = min(low[u], low[v]);
		}
		else if(vis[v]){
			low[u] = min(low[u], dfn[v]);
		}
	}
	if(dfn[u] == low[u]){
		vis[u] = false;
		scc[u] = ++col_num;
		while(stk[top] != u){
			scc[stk[top]] = col_num;
			vis[stk[top--]] = false;
		}
		--top;
	}
}

int main(){
	// initalize graph
	for(int i = 1; i <= n; i++){
		if(!dfn[i]) tarjan(i);
	}
}

- 「割边」（桥）

- 何为「割边」

在无向图中，如果把一条边删掉，导致这个图的极大联通子图数量增加，那么这条边就叫「割边」，也称作「桥」。

比如，下图：

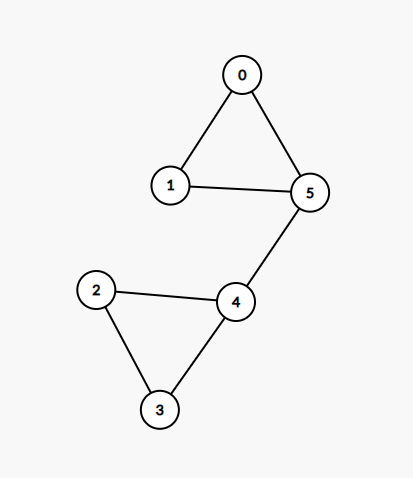
割去 \(4 \leftrightarrow 5\) 这一条边后，整个图被分成了两部分，联通块数量增加。

可以证明，整个图只有这一条割边。

- Tarjan 求割边

我们还是来定义一下 \(\text{dfn}\) 和 \(\text{low}\) 的含义。

• \(\text{dfn}\)：时间戳，表示在 dfs 树中是第几个被访问到的。

• \(\text{low}\)：追溯值数组，表示以 \(x\) 为根的搜索树上的点以及通过一条不在搜索树上的边能达到的结点中的最小编号。

我们在访问到节点 \(u\) 时，初始化 \(\text{dfn}_u=\text{low}_u=dfs\_num\)，表示它能追溯到他自己。和 Tarjan 求 scc 不同，求割边不需要维护手工栈。

然后我们接着访问它下面的一个节点：

1. 它没被访问过，就先 \(\text{dfs}(v)\)，对他进行深搜，并在回溯过程中以 \(\text{low}_v\) 更新 \(\text{low}_u\)（因为 \(v\) 可以访问到的节点 \(u\) 一定也可以访问到）。
2. 它被访问过，且不是它在 dfs 树上的父节点，根据 \(\text{low}\) 的定义，用 \(\text{dfn}_v\) 更新 \(\text{low}_u\)。

接下来我们想一想什么时候 \(u \leftrightarrow v\) 这条边是割边。

显然，如果一条边连接的 \(u,v\) 有 \(\text{low}_v>\text{dfn}_u\)，就说明 \(v\) 能访问到的最早的节点还比 \(u\) 晚。这说明如果 \(v\) 想到 \(u\)，只能通过 \(u \leftrightarrow v\) 这条边，于是这条边是割边。

- 代码实现（以 UVA796 为例）

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 5;
const int M = 1e6 + 5;

int dfn[N], low[N], dfs_num;
bool bridge[M];

struct graph{
	int to, next;
}G[N];
int head[N], cnt;
void addEdge(int u, int v){
	G[++cnt] = {v, head[u]}; head[u] = cnt;
}
vector<pair<int,int> > cut;

void tarjan(int u, int fa){
	dfn[u] = low[u] = ++dfs_num;
	for(int i = head[u]; i; i = G[i].next){
		int v = G[i].to;
		if(!dfn[v]){
			tarjan(v, u);
			if(low[v] > dfn[u]){
				bridge[i] = bridge[i ^ 1] = true;
				cut.push_back({min(u, v), max(u, v)});
			}
			low[u] = min(low[u], low[v]);
		}
		else if(v != fa){
			low[u] = min(low[u], dfn[v]);
		}
	}
}

void solve();

int n;

int main(){
	while(~scanf("%d", &n))
		solve();
}

void solve(){
	vector<pair<int, int> > ().swap(cut);
	memset(head, 0, (n + 5) * sizeof head[0]);
	memset(dfn, 0, (n + 5) * sizeof dfn[0]);
	memset(low, 0, (n + 5) * sizeof low[0]);
	memset(bridge, 0, (cnt + 5) * sizeof bridge[0]);
	cnt = 1;
	for(int i = 1; i <= n; i++){
		int u, k;
		scanf("%d (%d)", &u, &k); ++u;
		for(int j = 1; j <= k; j++){
			int v;
			scanf("%d", &v); ++v;
			addEdge(u, v);
			addEdge(v, u);
		}
	}
	for(int i = 1; i <= n; i++){
		if(!dfn[i]) tarjan(i, 0);
	}
	sort(cut.begin(), cut.end());
	printf("%d critical links\n", (int)cut.size());
	for(auto edge: cut) printf("%d - %d\n", edge.first - 1, edge.second - 1);
	putchar('\n');
}

- 「割点」（割顶）

- 何为「割点」

在无向图中，如果把一个点及其连到他的所有边删掉，导致这个图的极大联通子图数量增加，那么这条边就叫「割点」，也称作「割顶」。

例如下图：

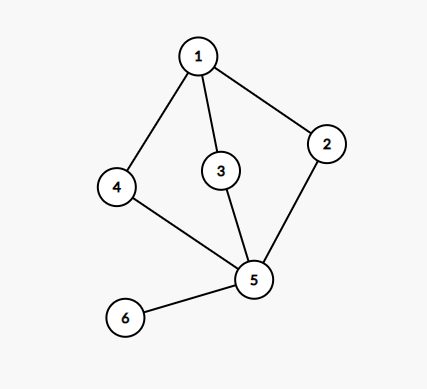
我们看到，把 \(5\) 删掉之后，整个图被分成了 \(\{1,4,3,2\},\{6\}\) 两个部分，联通块数量增加，所以 \(5\) 是割点。

可以证明，整个图只有 \(5\) 是割点。

- Tarjan 求割点

• \(\text{dfn}\)：时间戳，表示在 dfs 树中是第几个被访问到的。

• \(\text{low}\)：追溯值数组，表示以 \(x\) 为根的搜索树上的点以及通过一条不在搜索树上的边能达到的结点中的最小编号。

我们在访问到节点 \(u\) 时，初始化 \(\text{dfn}_u=\text{low}_u=dfs\_num\)，表示它能追溯到他自己。和 Tarjan 求割边类似的，求割边不需要维护手工栈。

然后我们接着访问它下面的一个节点：

1. 它没被访问过，就先 \(\text{dfs}(v)\)，对他进行深搜，并在回溯过程中以 \(\text{low}_v\) 更新 \(\text{low}_u\)（因为 \(v\) 可以访问到的节点 \(u\) 一定也可以访问到）。
2. 它被访问过，且不是它在 dfs 树上的父节点，根据 \(\text{low}\) 的定义，用 \(\text{dfn}_v\) 更新 \(\text{low}_u\)。

这里不可以用 \(\text{low}_v\) 更新 \(\text{low}_u\)！！！

如果之前的 \(\text{low}_v\) 是经过 \(u\) 的祖先节点的，那么 \(\text{low}_v\) 就不能算是 \(\text{low}_u\) 的可能情况（因为 \(\text{low}_u\) 要通过一条不在搜索树上的边），而 \(\text{dfn}_v\) 是确定的，可以更新。

接下来我们想一想什么时候 \(u \leftrightarrow v\) 这条边上的 \(u\) 是割点。

分情况：

1. \(u\) 是当前搜索树的根节点，那么，如果它在搜索树上有两个及以上的子树，它肯定是割点。因为割去它，一个子树必定无法到达另一个子树。

2. \(u\) 不是根节点，那么如果 \(\text{low}_v \ge \text{dfn}_u\)，说明 \(v\) 能追溯到的最早的节点顶多是 \(u\) 了，割去 \(u\) 会使它访问不到上面的节点。那么 \(u\) 是割点。

- 代码实现（以 洛谷 P3388 为例）

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 5;
const int M = 1e6 + 5;

int dfn[N], low[N], dfs_num;
bool cut[N];
vector<int> G[N];
int n, m, cut_num;

void tarjan(int u, int fa){
	int son = 0;
	dfn[u] = low[u] = ++dfs_num;
	for(auto &v: G[u]){
		if(!dfn[v]){
			++son;
			tarjan(v, u);
			low[u] = min(low[u], low[v]);
			if(u != fa && low[v] >= dfn[u]) cut[u] = true;
		}
		else if(v != fa) low[u] = min(low[u], dfn[v]);
	}
	if(u == fa && son >= 2) cut[u] = true;
}

int main(){
	scanf("%d %d", &n, &m);
	for(int i = 1; i <= m; i++){
		int u, v;
		scanf("%d %d", &u, &v);
		G[u].push_back(v);
		G[v].push_back(u);
	}
	for(int i = 1; i <= n; i++)
		if(!dfn[i]) tarjan(i, i);
	for(int i = 1; i <= n; i++)
		if(cut[i]) cut_num++;
	printf("%d\n", cut_num);
	for(int i = 1; i <= n; i++)
		if(cut[i]) printf("%d ", i);
}

- 「边双联通分量」

- 何为「边双联通分量」

如果对于原图的一个联通分量 \(G' \in G\)，无论哪一条边被删除后，这个分量中的任意两个点依然两两可达，那么我们就称 \(G'\) 为「边双联通分量」。

- Tarjan 求边双联通分量

显然，一个边双联通分量中不存在割边，因为如果有割边的话两个分量就不会联通。

那么我们要做的事就很清晰了：先把割边删除，然后对于每一个没有上色的点 dfs，并对其联通分量染色。最后染成一色的就是一个边双。

实现代码时有一个小技巧：不需要真正地把割边删除，只需要标记这条边不可走即可。

- 代码实现（以 洛谷 P8436 为例）

#include <bits/stdc++.h>
using namespace std;

const int N = 6e5 + 5;
const int M = 6e6 + 5;

int dfn[N], low[N], dfs_num;
bool bridge[M], vis[N];
int n, m, scc_num;
vector<vector<int> > cut;

struct graph{
	int to, next;
}G[M];
int head[N], cnt = 1;
void addEdge(int u, int v){G[++cnt] = {v, head[u]}; head[u] = cnt;}

void tarjan(int u, int fa){
	dfn[u] = low[u] = ++dfs_num;
	for(int i = head[u]; i; i = G[i].next){
		int v = G[i].to;
		if(!dfn[v]){
			tarjan(v, u);
			low[u] = min(low[u], low[v]);
			if(low[v] > dfn[u])
				bridge[i] = bridge[i ^ 1] = true;
		}
		else if(v != fa) low[u] = min(low[u], dfn[v]);
	}
}

void dfs(int u, int col){
	vis[u] = true;
	cut[col - 1].push_back(u);
	for(int i = head[u]; i; i = G[i].next){
		int v = G[i].to;
		if(vis[v] || bridge[i]) continue;
		dfs(v, col);
	}
}

int main(){
	scanf("%d %d", &n, &m);
	for(int i = 1; i <= m; i++){
		int u, v;
		scanf("%d %d", &u, &v);
		if(u == v) continue;
		addEdge(u, v);
		addEdge(v, u);
	}
	for(int i = 1; i <= n; i++)
		if(!dfn[i]) tarjan(i, i);
	for(int i = 1; i <= n; i++){
		if(!vis[i]){
			++scc_num;
			cut.push_back(vector<int>());
			dfs(i, scc_num);
		}
	}
	printf("%d\n", scc_num);
	for(int i = 0; i < scc_num; i++){
		printf("%d ", cut[i].size());
		for(auto vertex: cut[i]) printf("%d ",vertex);
		printf("\n");
	}
}

- 「点双联通分量」

- 何为「点双联通分量」

如果对于原图的一个联通分量 \(G' \in G\)，无论哪个点被删除后，这个分量中的任意两个点依然两两可达，那么我们就称 \(G'\) 为「点双联通分量」。

容易看出，对于原图 \(G\)，每个割点都存在于至少两个联通分量中。

割点连接着原图的两个（或以上）部分，必然每个部分都应将它包含。

- Tarjan 求点双联通分量

显然，一个点双联通分量中不存在割点，因为如果有割点的话删去之后两个分量就不会联通。

那么我们要做的事就很清晰了：先把找出割点，然后对于每一个没有上色的点 dfs，并对其联通分量染色，注意到了割点就不能往下走了。最后染成一色的就是一个点双。

注意每个割点会被染色多次，所以你只需要在 dfs 过程中统计即可。

- 代码实现

// 根据边双改改喵
// 根据边双改改谢谢喵

- Reference

• https://oi-wiki.org/graph/scc/

• \(\texttt{[1]}\)：https://www.cnblogs.com/shadowland/p/5872257.html，感谢 SHHHS 大佬让我懂得了 Tarjan。

• \(\texttt{[2]}\)：关于这里为什么最好用 \(\text{low}_v\) 更新 \(\text{low}_u\)，下文讲到割点的时候会讲。