LCA学习笔记（原洛谷文章）

本文原发布时间：\(\texttt{2022-05-21 14:11:52}\)

简介

最经公共祖先 \(\operatorname{LCA}(a,b)=c\)，指的是在一棵树上节点 \(a\) 与 \(b\) 之间离两个点最近的一个点 \(c\)，使得 \(c\) 是它们的祖先。

比如说，下面这棵树：

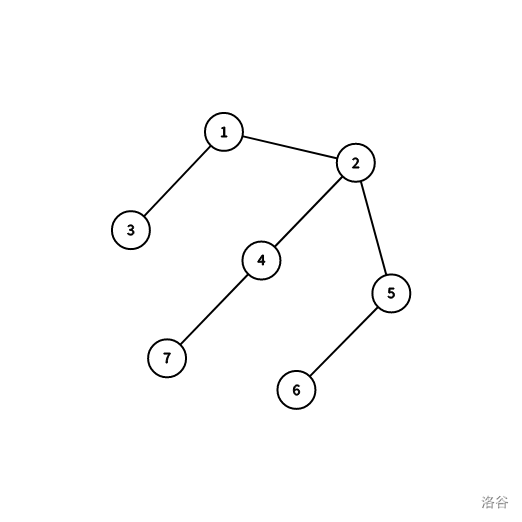
那么 \(\operatorname{LCA}(6,7)=2\)，注意，不是 \(1\)。

例题(P3379 【模板】最近公共祖先）

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数 \(N,M,S\)，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来 \(N-1\) 行每行包含两个正整数 \(x, y\)，表示 \(x\) 结点和 \(y\) 结点之间有一条直接连接的边（数据保证可以构成树）。

接下来 \(M\) 行每行包含两个正整数 \(a, b\)，表示询问 \(a\) 结点和 \(b\) 结点的最近公共祖先。

输出格式

输出包含 \(M\) 行，每行包含一个正整数，依次为每一个询问的结果。

提示说明

对于 \(30\%\) 的数据，\(N\leq 10\)，\(M\leq 10\)。

对于 \(70\%\) 的数据，\(N\leq 10000\)，\(M\leq 10000\)。

对于 \(100\%\) 的数据，\(N\leq 500000\)，\(M\leq 500000\)。

2021/10/4 数据更新 @fstqwq：应要求加了两组数据卡掉了暴力跳。

求法

0.暴力法

思路很简单。

首先预处理深度，询问时先统一深度，然后逐级上推即可。

最差时间复杂度 \(O(NM)\) 只能通过 \(70\%\) 的数据。

1.倍增法

倍增法本质上是对暴力法的优化。

首先，我们不必一个一个跳，可以指数级跳跃，效率大幅度提升。

具体如下：

首先，预处理节点 \(i\) 的第 \(2^{j}\) 级祖先 \(\operatorname{FA}[i][j]\)，当然，还有深度。

询问时，先调整深度，然后倍增跳跃即可。

时间复杂度 \(O(N+M\log N)\)，可以通过所有数据。

代码

我用的是链式前向星存图。

#include <bits/stdc++.h>
using namespace std;
struct edge{
	int nxt,to,w;
} tree[500005*2];
int head[500005],ec;
void add(int from,int to,int weight){
	tree[++ec].nxt=head[from];
	tree[ec].to=to;
	tree[ec].w=weight;
	head[from]=ec;
}
int fa[500005][55],deep[500005],lg2[500005];
inline void initlog(int n){
	lg2[1]=0;
	lg2[2]=1;
	for(int i=3;i<=n;i++){
		lg2[i]=lg2[i>>1]+1;
	}
}
void dfs(int now,int parent){
	fa[now][0]=parent;
	deep[now]=deep[parent]+1;
	for(int i=1;(1<<i)<=deep[now];i++){
		fa[now][i]=fa[fa[now][i-1]][i-1];
	}
	for(int i=head[now];i;i=tree[i].nxt){
		if(tree[i].to != parent){
			dfs(tree[i].to,now);
		}
	}
}
int lca(int x,int y){
	if(deep[x]<deep[y]){
		swap(x,y);
	}
	while(deep[x]!=deep[y]){
		x=fa[x][lg2[deep[x]-deep[y]-1]];
	}
	if(x==y){
		return x;
	}
	for(int k=lg2[deep[x]];k>=0;k--){
		if(fa[x][k]!=fa[y][k]){
			x=fa[x][k];
			y=fa[y][k];
		}
	}
	return fa[x][0];
}
int n,m,s;
int main(){
	cin>>n>>m>>s;
	for(int i=1,u,v;i<=n-1;i++){
		cin>>u>>v;
		add(u,v,114514);
		add(v,u,1919810);
	}
	initlog(n);
	dfs(s,0);
	for(int i=1,arcka,akioi;i<=m;i++){
		cin>>arcka>>akioi;
		cout<<lca(arcka,akioi)<<endl;
	}
	return 0;
}

AC in Luogu

Tarjan

埋坑。

例题

(原创)Game2:简单树上问题

题目描述

给你一个 \(N\) 顶点的树，有 \(M\) 个询问，每次询问给出两个节点 \(u,v\) 求这两个点之间的最短距离。

输入格式

第一行为 \(N,M\)

接下来 \(N-1\) 行，每行三个整数 \(u,v,w\)，表示一条从 \(u\) 到 \(v\) 的边，请忽略 \(w\)。

然后 \(M\) 行，每行两个整数 \(u,v\)。

输出格式

对于每一个询问，输出一个整数，表示答案。

提示

\(N,M = 100000,1 \le u,v,w \le N\)

时间限制 \(600\operatorname{ms}\)，空间限制 \(50\operatorname{MB}\)。

造数据程序

from cyaron import *
n = 100000
m=n
for i in range(1, 25):
    test = IO(file_prefix="data/test",data_id=i)
    test.input_writeln(n,m)
    graph=Graph.tree(n)
    test.input_writeln(graph)
    for i in range(m):
        test.input_writeln(randint(1,n),randint(1,n))
    test.output_gen("C:/Users/stu01/Documents/hh.exe")

思路

这道题可以直接用倍增LCA解决，因为：

\[\operatorname{Dis}(u,v)=\operatorname{Deep}(u)+\operatorname{Deep}(v)-2 \times \operatorname{Deep}(\operatorname{LCA}(u,v))
\]

代码

#include <bits/stdc++.h>
using namespace std;
struct edge{
	int nxt,to,w;
} tree[500005*2];
int head[500005],ec;
void add(int from,int to,int weight){
	tree[++ec].nxt=head[from];
	tree[ec].to=to;
	tree[ec].w=weight;
	head[from]=ec;
}
int fa[500005][55],deep[500005],lg2[500005];
inline void initlog(int n){
	lg2[1]=0;
	lg2[2]=1;
	for(int i=3;i<=n;i++){
		lg2[i]=lg2[i>>1]+1;
	}
}
void dfs(int now,int parent){
	fa[now][0]=parent;
	deep[now]=deep[parent]+1;
	for(int i=1;(1<<i)<=deep[now];i++){
		fa[now][i]=fa[fa[now][i-1]][i-1];
	}
	for(int i=head[now];i;i=tree[i].nxt){
		if(tree[i].to != parent){
			dfs(tree[i].to,now);
		}
	}
}
int lca(int x,int y){
	if(deep[x]<deep[y]){
		swap(x,y);
	}
	while(deep[x]!=deep[y]){
		x=fa[x][lg2[deep[x]-deep[y]-1]];
	}
	if(x==y){
		return x;
	}
	for(int k=lg2[deep[x]];k>=0;k--){
		if(fa[x][k]!=fa[y][k]){
			x=fa[x][k];
			y=fa[y][k];
		}
	}
	return fa[x][0];
}
int n,m,s=1;
int main(){
	cin>>n>>m;
	for(int i=1,u,v,w;i<=n-1;i++){
		cin>>u>>v>>w;
		add(u,v,114514);
		add(v,u,1919810);
	}
	initlog(n);
	dfs(s,0);
	for(int i=1,arcka,akioi;i<=m;i++){
		cin>>arcka>>akioi;
		cout<<deep[arcka]+deep[akioi]-2*deep[lca(arcka,akioi)]<<endl;
	}
	return 0;
}

P4281 [AHOI2008]紧急集合 / 聚会 | LibreOJ10136. 「一本通 4.4 练习 3」聚会

简要题意

对于一个有根树，有 \(n\) 个节点，有 \(m\) 个询问，每次询问提供三个节点 \(x,y,z\)，求一点 \(p\)，使得 \(c=\operatorname{Dis}(x,p)+\operatorname{Dis}(y,p)+\operatorname{Dis}(z,p)\) 最小，输出 \(p\) 和 \(c\)。（\(\operatorname{Dis}(u,v)\) 表示 \(u\) 到 \(v\) 的最短路径长度）

对于 \(100\%\) 的数据，\(1\leq x,y,z\leq n\leq 5\times10^5\)，\(1\leq m\leq 5\times 10^5\)。

思路

首先先来口胡一个结论，不重复的节点才是最优解。

然后就是算长度了，由于我们是三个点走到一个，那么就是这个：

\[\begin{aligned}
\operatorname{Dis}(x,y,z)=
\operatorname{Deep}(x)+
\operatorname{Deep}(y)+
\operatorname{Deep}(z)-\\
\operatorname{Deep}(\operatorname{LCA}(x,y))-
\operatorname{Deep}(\operatorname{LCA}(x,z))-
\operatorname{Deep}(\operatorname{LCA}(y,z))
\end{aligned}
\]

自己Hand推

时间复杂度 \(O(n+m\log n)\)。注意，本题需要卡常。

代码

#include <bits/stdc++.h>
using namespace std;
struct edge{
	int nxt,to,w;
} tree[500005*2];
int head[500005],ec;
void add(int from,int to,int weight){
	tree[++ec].nxt=head[from];
	tree[ec].to=to;
	tree[ec].w=weight;
	head[from]=ec;
}
int fa[500005][55],deep[500005],lg2[500005];
inline void initlog(int n){
	lg2[1]=0;
	lg2[2]=1;
	for(int i=3;i<=n;i++){
		lg2[i]=lg2[i>>1]+1;
	}
}
void dfs(int now,int parent){
	fa[now][0]=parent;
	deep[now]=deep[parent]+1;
	for(int i=1;(1<<i)<=deep[now];i++){
		fa[now][i]=fa[fa[now][i-1]][i-1];
	}
	for(int i=head[now];i;i=tree[i].nxt){
		if(tree[i].to != parent){
			dfs(tree[i].to,now);
		}
	}
}
int lca(int x,int y){
	if(deep[x]<deep[y]){
		swap(x,y);
	}
	while(deep[x]!=deep[y]){
		x=fa[x][lg2[deep[x]-deep[y]-1]];
	}
	if(x==y){
		return x;
	}
	for(int k=lg2[deep[x]];k>=0;k--){
		if(fa[x][k]!=fa[y][k]){
			x=fa[x][k];
			y=fa[y][k];
		}
	}
	return fa[x][0];
}
int n,m;
inline int cd(int a,int b,int LCA){
	return deep[a]+deep[b]-2*deep[LCA];
}
int main(){
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,u,v;i<=n-1;i++){
		cin>>u>>v;
		add(u,v,114514);
		add(v,u,1919810);
	}
	initlog(n);
	dfs(1,0);
	while(m--){
		int x,y,z;
		cin>>x>>y>>z;
		int l1=lca(x,y),l2=lca(x,z),l3=lca(y,z),ll=0;
		if(l1==l2)ll=l3;
		else if(l1==l3)ll=l2;
		else ll=l1;
		cout<<ll<<' ';
		cout<<(deep[x]+deep[y]+deep[z]-deep[l1]-deep[l2]-deep[l3])<<'\n';
	}
	return 0;
}

AC in LibreOJ

AC in Luogu