One-Shot Transfer Learning of Physics-Informed Neural Networks
本文提出了一种将迁移学习应用到PINN的方法。可以极大的缩短训练PINN所用的时间,目前,PINN所需要的训练次数往往都在成千上万次,
作者通过批量训练PINN,来学习丰富的潜在空间用来执行迁移学习。主要是冻结网络的隐藏层,只微调最后一个线性层。这样可以将神经网络的推理速度快好几个数量级。对于线性问题,本文涉及的几个实验都仅仅只需要几秒钟就可以完成训练,此外,非线性问题依旧可以使用梯度下降进行优化,这就类似于一般的迁移学习了。
首先,关于本文模型结构,可以给一个大概的描述,如下图:

不同于一般的PINN结构,本文的输出层的大小是可以根据参与训练的方程的个数进行调整的。但这些方程都是同一类的,具有不同的非齐次项,初始条件,边界条件等。比如,薛定谔方程,因为同时训练三个不同的参数,取n=3,输出层就有6的神经元。(因为薛定谔方程的解是复值解,本身就需要两个神经元)。因为没有找到代码,所以我猜测训练时,网络同时给输出三个解,分别带入各自的损失函数(也就是残差+边界),从而对网络进行优化。最后的微调阶段,对于一个新的方程,只调节最后一个线性层的大小,就可以快速精确的获得近似解。
现在我们看一下论文。本文发表在ICML2022。
摘要:作者首先说到,将迁移学习应用到求解PDE还未被充分探索,诚然,我还没有读到过类似的文章。对于线性的常微分和偏微分方程,作者提出一种一次性推断的迁移学习方法。这就意味着在求解新的方程时,无需重新训练整个网络。
介绍:目前关注PINN计算花费的论文还不是很多,PINN的训练是很慢的,自己的感觉是训练时对cpu要求比较高,收敛速度比较慢。因此作者使用迁移学习来解决这个问题,在一个任务上训练,并将模型转移到其他的任务上。具体的说,在一系列PDE上预训练的PINN,可以有效地用于求解新的微分方程。通过冻结预训练的PINN的隐藏层,求解同一系列的新的微分方程就简化于微调线性层。并且对于线性系统,甚至可以通过人工计算消除微调的必要,从而降低训练开销,大大减少训练时间。这也是本文将重点介绍的。
背景:ODE给定IC,传统下可以使用积分求解器求解。目前也可以使用PINN求解,损失函数如3式。使用神经网络,相比较于传统方法,可以消除维度灾难、避免累积误差等。但是,目前关于迁移学习的应用还比较少。
相关工作是机器学习关于求解PDE的发展历史。
方法:首先以ODE为例。定义一个神经网络去近似方程的解。换句话说,被参数化的神经网络,将输入t投影到一个高维的非线性隐层空间H,H是隐层空间和非线性激活函数的组合。然后,在潜在空间的线性组合,来获得最后的解。
为了训练网络,定义最后的权重层是多输出的。这样就可以同时训练多个方程(比如不同的微分算子,初始条件等)。捆绑训练允许我们 1 将训练集成到单个网络中,2 鼓励隐层状态H对于多个方程适用。
在推断时(对于一个新的任务),我们冻结隐藏层的参数,仅仅微调最后一个线性层。解可以被写成 H*W 的形式。那么,在面对新的问题是,损失就变成了4式。
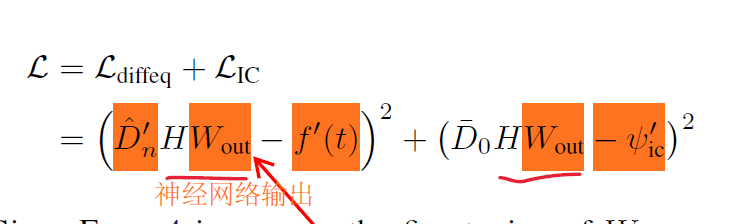
对于线性系统,W是可以直接计算的。
还有一个更直观的理解,我们把h看作一组非正交基,Wout是一组系数,即通过线性组合确定输出的近似函数。并且7式还可以进一步简化,因为前一项逆矩阵可以提前计算。总之,这样就可以免于计算梯度,因为没有涉及到进一步的训练。并且如果H足够好,就可以获得高精度的解。事实上,这个方法很依赖于矩阵的逆,如果有很大条件数时,会导致问题病态。实验中可以通过正则化和分解来解决。 对于非线性系统,最后的线性层只能使用微调得到了。
然后到了PDE,一样的过程,可以计算得到W。我们再来说一下H,作者认为,只有当H这组基能够很好的表示解空间时,才能获得准确的解(希望由H张成的子空间尽可能大)。因此,为了鼓励学到有代表性的隐空间,作者使用了一个网络来训练多个方程。
结果:
使用了四个不同的泊松方程训练,用两种方式测试。已知分析解。图1结果还不错。
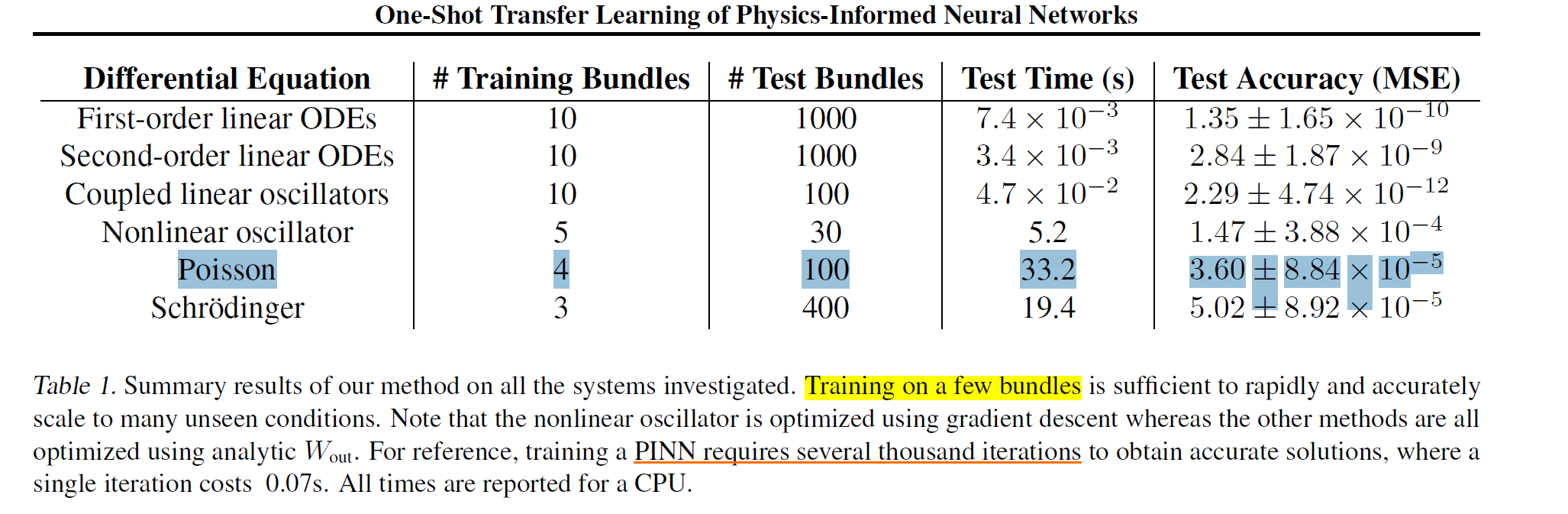
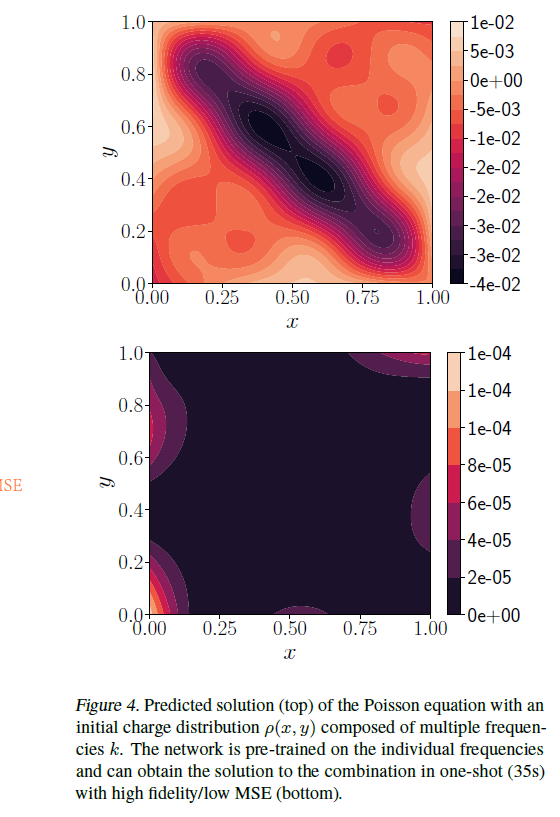
然后又考虑了薛定谔,使用三个方程训练,测试结果如下。
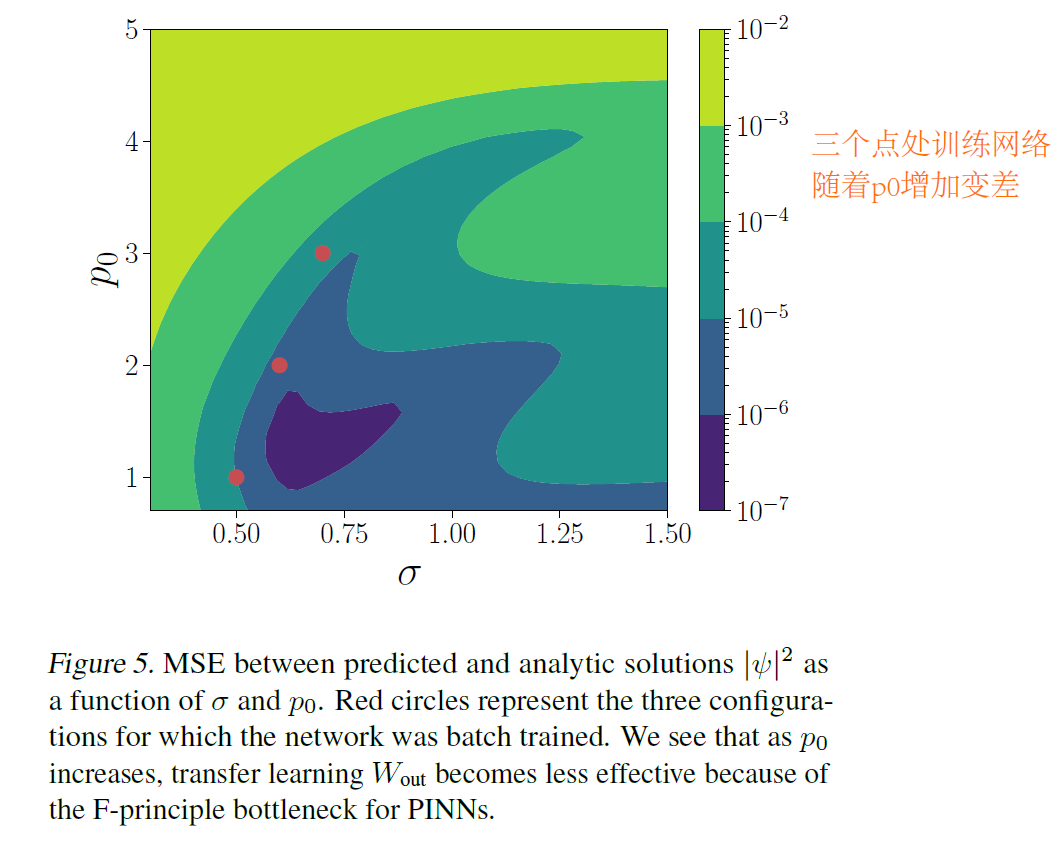
One-Shot Transfer Learning of Physics-Informed Neural Networks的更多相关文章
- 1506.01186-Cyclical Learning Rates for Training Neural Networks
1506.01186-Cyclical Learning Rates for Training Neural Networks 论文中提出了一种循环调整学习率来训练模型的方式. 如下图: 通过循环的线 ...
- Learning How To Code Neural Networks
原文:https://medium.com/learning-new-stuff/how-to-learn-neural-networks-758b78f2736e#.ly5wpz44d This i ...
- Coursera Deep Learning 2 Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization - week2, Assignment(Optimization Methods)
声明:所有内容来自coursera,作为个人学习笔记记录在这里. 请不要ctrl+c/ctrl+v作业. Optimization Methods Until now, you've always u ...
- Coursera Deep Learning 2 Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization - week1, Assignment(Initialization)
声明:所有内容来自coursera,作为个人学习笔记记录在这里. Initialization Welcome to the first assignment of "Improving D ...
- 吴恩达《深度学习》-课后测验-第一门课 (Neural Networks and Deep Learning)-Week 3 - Shallow Neural Networks(第三周测验 - 浅层神 经网络)
Week 3 Quiz - Shallow Neural Networks(第三周测验 - 浅层神经网络) \1. Which of the following are true? (Check al ...
- Coursera Deep Learning 2 Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization - week1, Assignment(Regularization)
声明:所有内容来自coursera,作为个人学习笔记记录在这里. Regularization Welcome to the second assignment of this week. Deep ...
- Coursera Deep Learning 2 Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization - week1, Assignment(Gradient Checking)
声明:所有内容来自coursera,作为个人学习笔记记录在这里. Gradient Checking Welcome to the final assignment for this week! In ...
- Coursera Deep Learning 2 Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization - week3, Hyperparameter tuning, Batch Normalization and Programming Frameworks
Tuning process 下图中的需要tune的parameter的先后顺序, 红色>黄色>紫色,其他基本不会tune. 先讲到怎么选hyperparameter, 需要随机选取(sa ...
- Coursera Deep Learning 2 Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization - week2, Optimization algorithms
Gradient descent Batch Gradient Decent, Mini-batch gradient descent, Stochastic gradient descent 还有很 ...
- Coursera, Deep Learning 2, Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization - week1, Course
Train/Dev/Test set Bias/Variance Regularization 有下面一些regularization的方法. L2 regularation drop out da ...
随机推荐
- SAP SPOOL_INTERNAL_ERROR
运行SE38程序 RSPO0041
- Windows 隐藏 远程桌面(连接栏)
当我们在使用远程桌面控制的时候,远程桌面工具栏遮挡视线很烦人.这时候就很有必要隐藏了! 1.全屏时显示连接栏 勾选去掉 这样子远程桌面上方的连接栏就消失了. 那么我们怎么打开呢?所以就要写下来记住了. ...
- 运行Java时报错:Error: opening registry key 'Software\JavaSoft\Java Runtime Environment'
卸载旧的JAVA JDK,安装新版的JDK时,运行cmd的java -version命令遇到这样的报错: Error: opening registry key 'Software\JavaSoft\ ...
- linux命令行大量零碎练习习题集-打包未整理
linux命令行大量零碎练习习题集-打包未整理最近看完了一本linux书籍,想着做题来检测和巩固一下,于是打算去买本linux命令集习题去做做.但是没有找到相关的书籍,于是只能在网上随便找找.但是很多 ...
- uni小程序保存base64图片
使用uni.getFileSystemManager().writeFile去下载base64图片<view class="share-btn" @click="s ...
- 使用ESP8266连接中文wifi
使用XCOM串口调试助手调试ESP8266时,想要连接学校的wifi,通过AT+CWLAP可以显示出附近所有wifi的列表,可是XCOM以ascii码格式显示文本,所以中文就乱码了. 一开始我不知道这 ...
- Mac下配置Groovy
官网:http://www.groovy-lang.org/ Step 1:下载Groovy 地址:https://groovy.apache.org/download.html 下载后解压 Step ...
- Spring框架1--IoC
Spring框架之IoC Spring的后处理器 待补充~ BeanFactoryPostProcessor BeanPostProcessor Bean的生命周期 具体可见图解:点击这里 补充: A ...
- java方法的笔记
方法 方法的概念 方法(method)是将具有独立功能的代码块组织成为一个整体,使其具有特殊功能的代码集 注意: 方法必须先创建才可以使用,该过程成为方法定义 方法创建后并不是直接可以运行的,需要手动 ...
- Excel如何按名字提取另一张表上数据(跨表查询)
1.Excel如何按名字提取另一张表上数据(跨表查询) 公式"=VLOOKUP(A3,[工资信息.xls]Sheet1!$A$3:$B$32,2,0)"原理. 1."A3 ...
