[排序算法] 简单选择排序 (C++)

简单选择排序原理

简单选择排序 SelectSort 是一种十分直观地排序方法。其原理是每次从未排序的元素中找到当前最小的元素，放在当前未排序序列的首位。一直重复操作直至最后未排序的元素个数为 0，即完成了排序。

---

核心代码(Old version)

这个代码是我在大一的时候学习的时候写的，很明显多做了很多次交换操作。

这个核心代码的想法是: 每次将比当前未排序序列的首位元素较小的数据元素，交换到首位，最后每一趟比较都会将当前最小的元素交换到未排序序列的首位。重复这样的操作，即可完成排序。(那个时候太菜了，完全没有注意到多做了很多次无用的交换嘤嘤嘤)

void SelectSort(vector<int> &v){
    int n = v.size();
    for(int i = 0; i < n - 1; i++)
	for(int j = i + 1; j < n; j++)
	    if(v[i] > v[j])
		swap(v[i], v[j]);
}

后来我发现，其实只需要定义一个 min 用于记录当前未排序序列中最小元素的位置就可以了。所以之后我有了新的简单选择排序代码。

---

简单选择排序(New version)动态演示

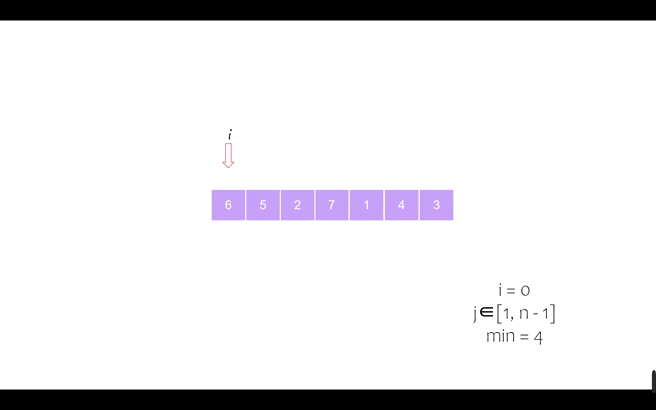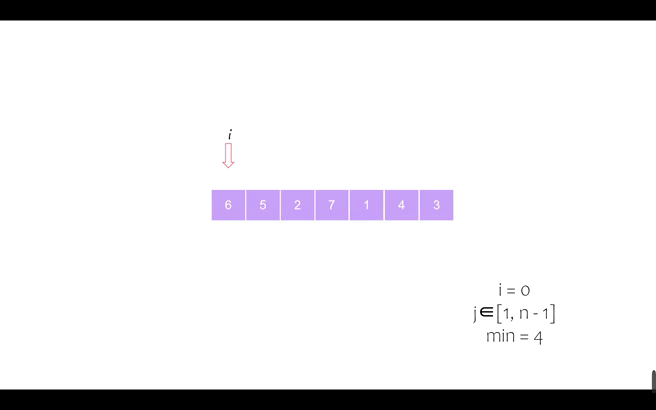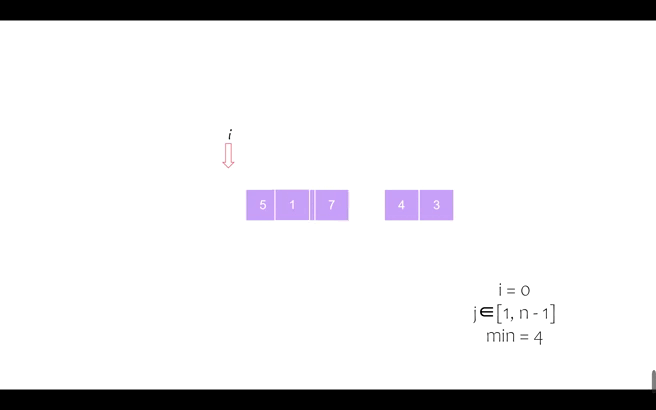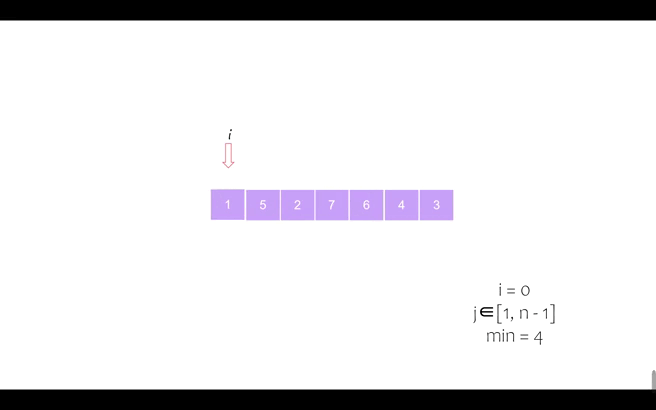
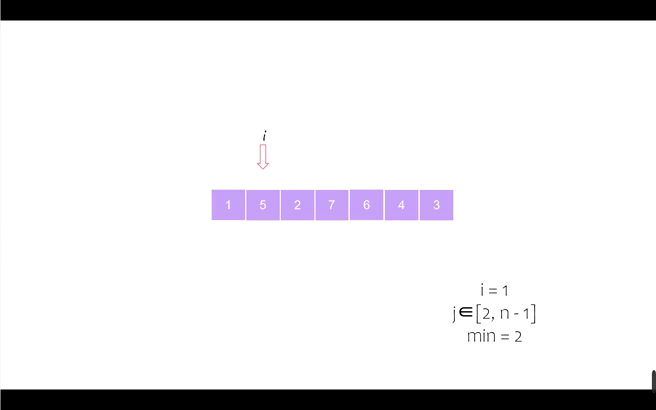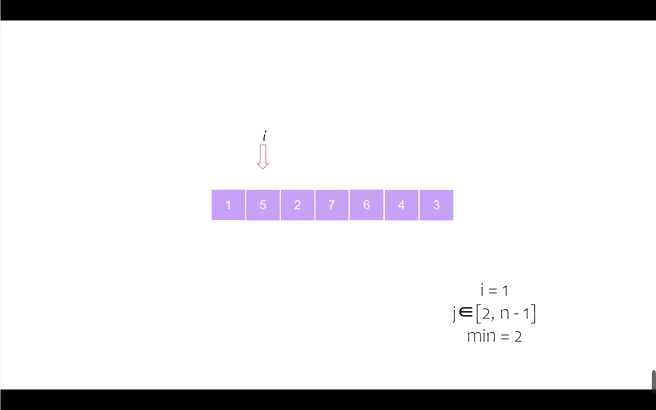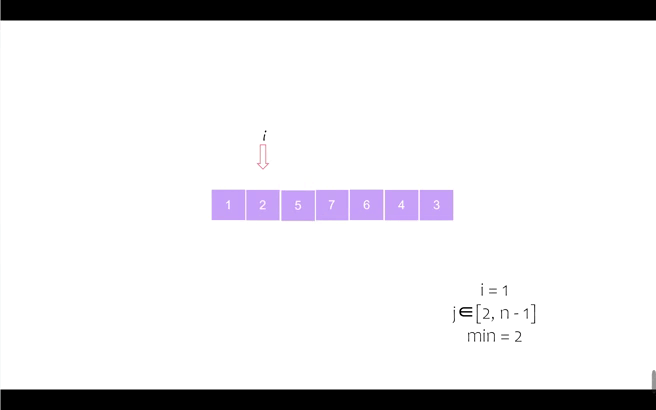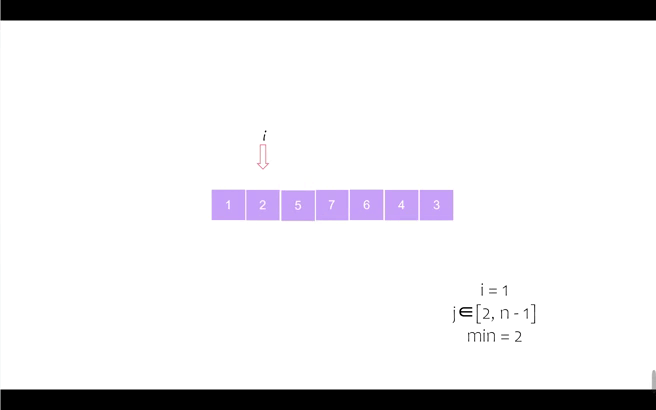
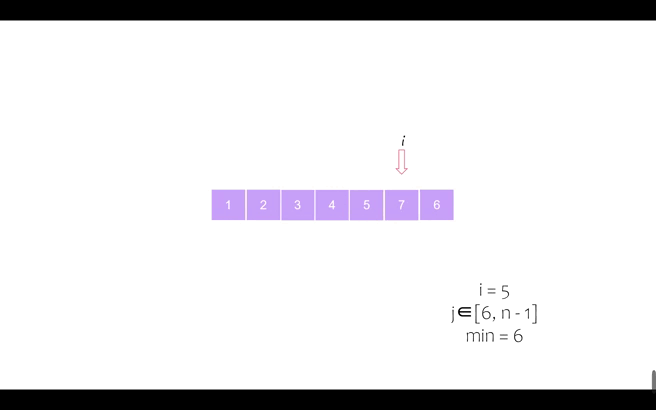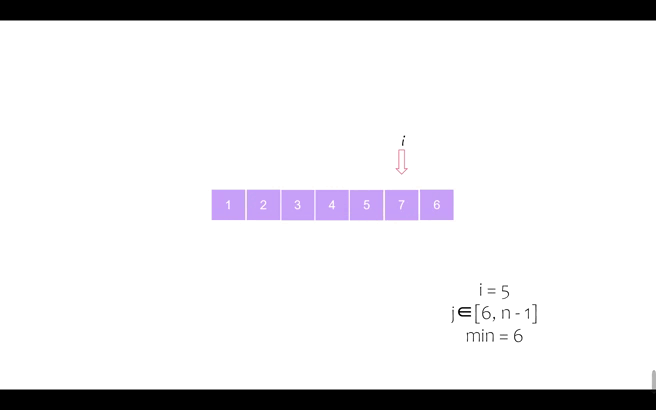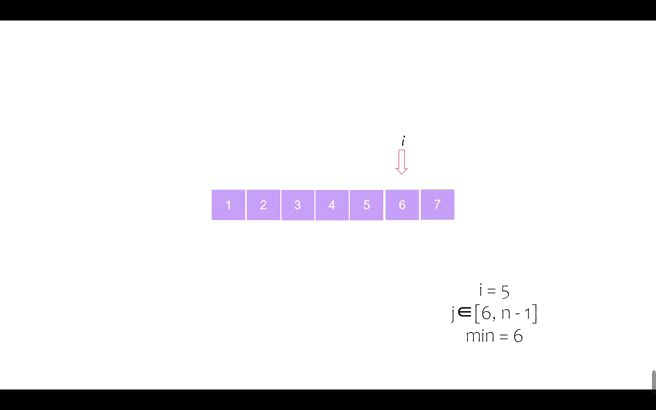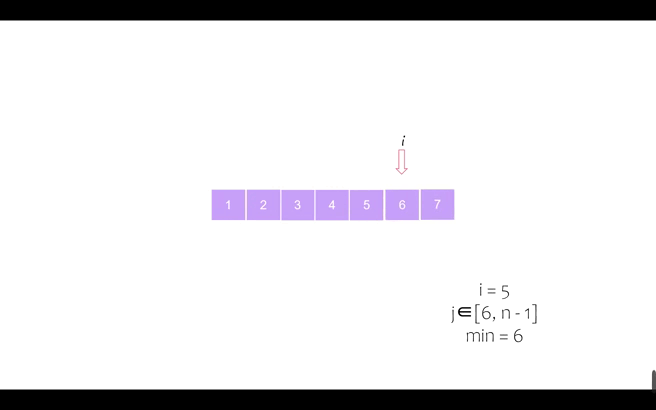
我们以序列 [6, 5, 2, 7, 1, 4, 3] 为例进行动态演示

第一个位置

第二个位置

第三个位置

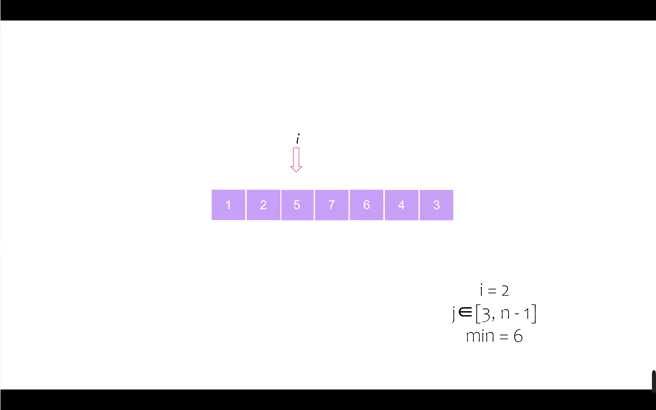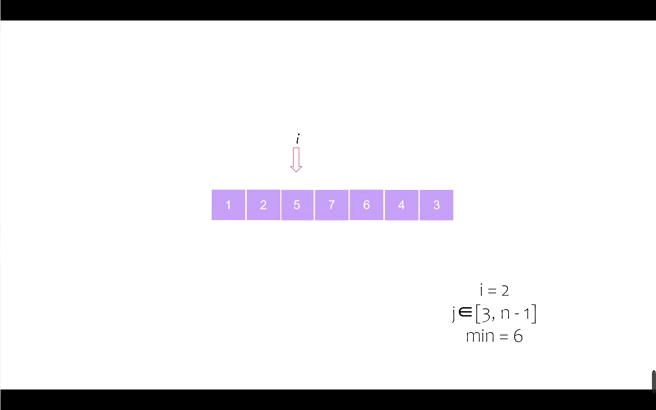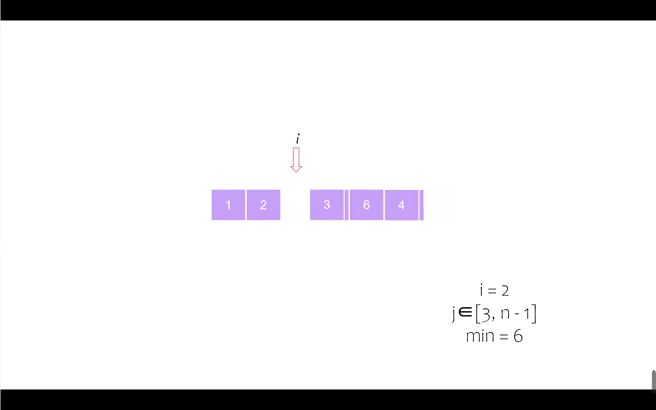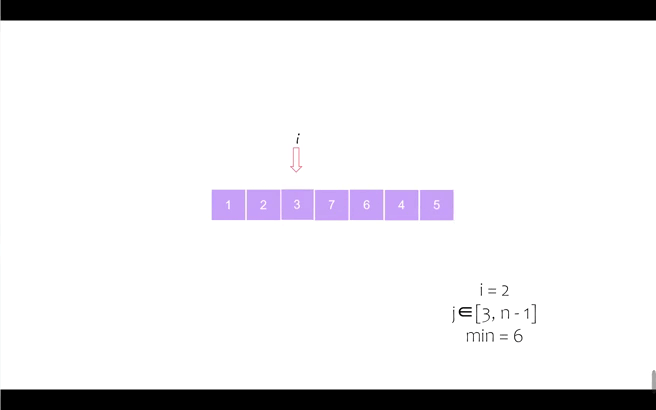
第四个位置

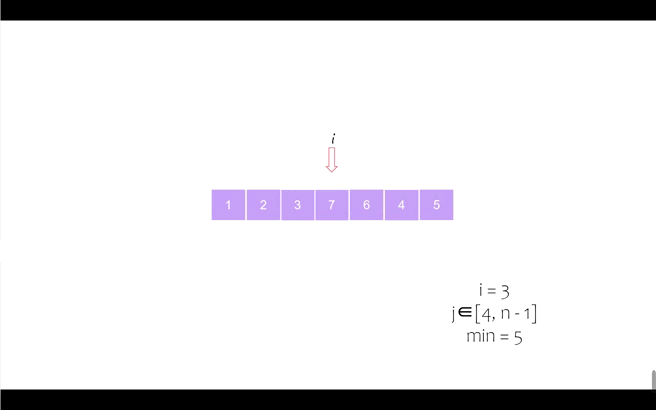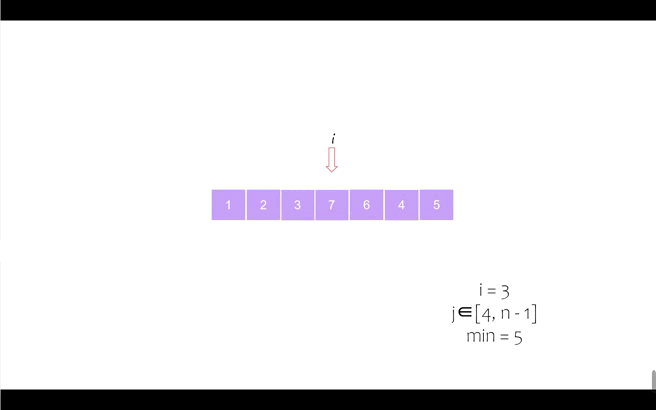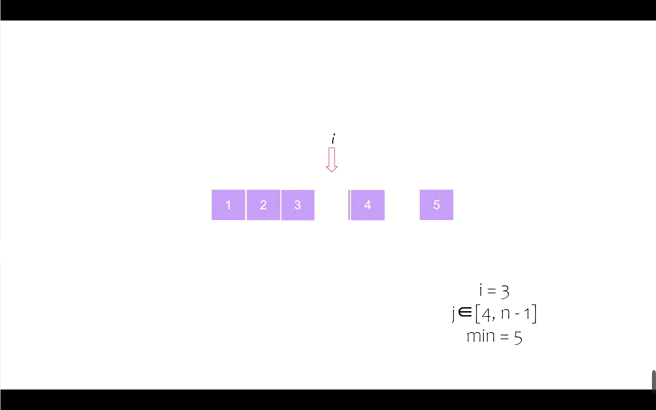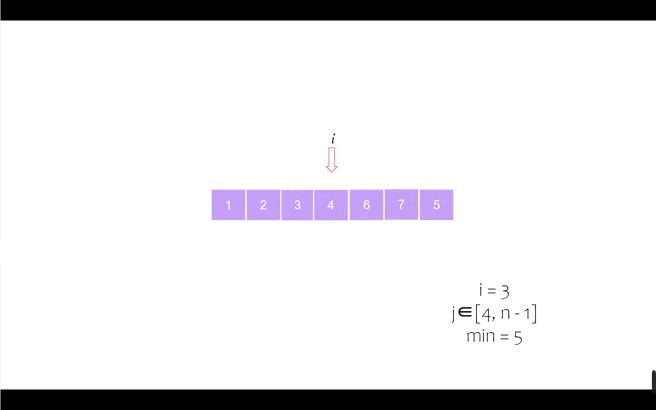
第五个位置

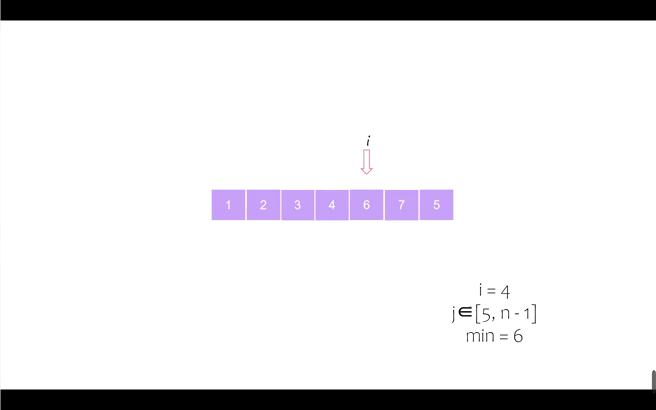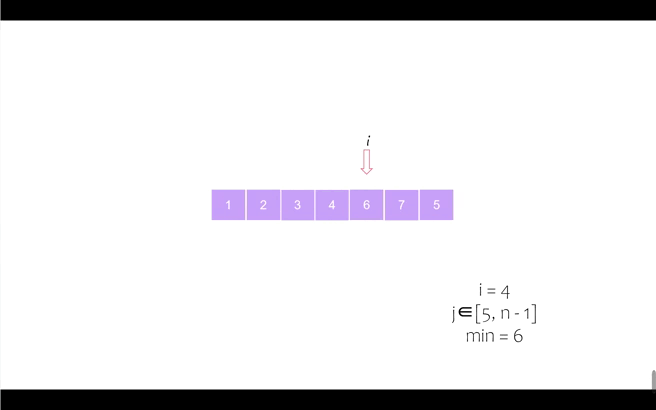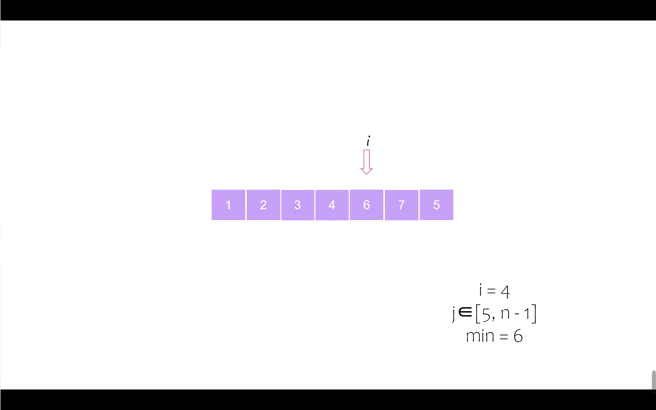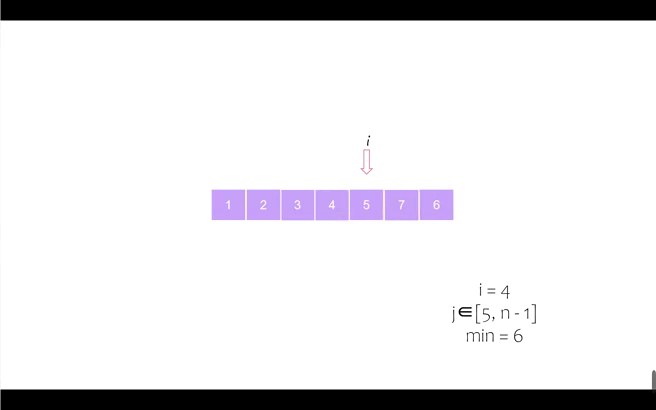
第六个位置（同时最后一个位置也完成归位，排序完成）

---

核心代码 (New version)

void SelectSort(vector<int> &v){
    int n = v.size();
    for(int i = 0; i < n - 1; i++){
	int min = i;
	for(int j = i + 1; j < n; j++){
	    if(v[min] > v[j]){
		min = j;
	    }
	}
	if(min != i)
	    swap(v[i], v[min]);
    }
}

此时每次都只是记录当前未排序序列最小值的位置，最后再进行交换。

---

完整程序源代码

#include<iostream>
#include<vector>
#include<ctime>
using namespace std;

void SelectSort(vector<int> &v){
    int n = v.size();
    for(int i = 0; i < n - 1; i++){
        int min = i;
	for(int j = i + 1; j < n; j++){
	    if(v[min] > v[j]){
		min = j;
	    }
	}
	if(min != i)
	    swap(v[i], v[min]);
    }
}

void show(vector<int> &v){
    for(auto &x : v)
        cout<<x<<" ";
    cout<<endl;
}

main(){
    vector<int> v;
    srand((int)time(0));
    int n = 50;
    while(n--)
        v.push_back(rand() % 100 + 1);
    show(v);

    SelectSort(v);

    cout<<endl<<endl;
    show(v);
}

---

程序运行结果图