数据结构Java版之遍历二叉树（六）

　　二叉树是我们在程序中用的最多的一种树（个人观点）。最简单的一个二叉树是由一个根节点，两个子节点（一左一右成左右孩子节点）组成。二叉树是数组和链表的结合，即包含了数组的快速查找优点，又包含了链表的快速添加删除的优点。熟练掌握二叉树的遍历方法是很有必要的。下面来介绍一下基于二叉树的四种遍历方式。

　　下面我们以一个棵简单的二叉树为例来说明四种遍历：

　　

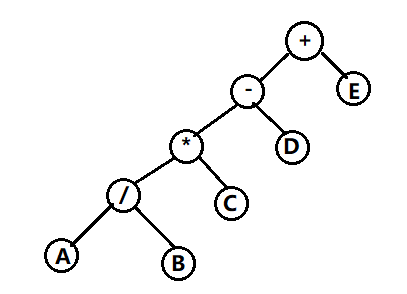
创建树节点类：

    //树节点
    class TreeNode {
        public char val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(char x) {
            val = x;
        }
    }

　　中序遍历：

　　先遍历左孩子节点---根节点---右孩子节点

//中序遍历        左-根-右    （前中后：根的位置）
public void InOrder(TreeNode current){
    if(current != null) {
        InOrder(current.left);
        Visit(current);
        InOrder(current.right);
    }
}

　　前序遍历：

　　遍历根节点---左孩子节点---右孩子节点

//前序遍历        根-左-右
public void PreOrder(TreeNode current){
    if(current != null) {
        Visit(current);
        InOrder(current.left);
        InOrder(current.right);
    }
}

　　后序遍历：

　　遍历左孩子节点---右孩子节点---根节点

    //后续遍历        左-右-根
    public void PostOrder(TreeNode current){
        if(current != null) {
            InOrder(current.left);
            InOrder(current.right);
            Visit(current);
        }
    }

　　层序遍历：

　　同一层节点从左往右依次遍历。

    //层序遍历        同一层节点从左往右依次遍历　　FIFO
    public void LevelOrder(TreeNode current){
        List<TreeNode> q = new ArrayList<TreeNode>();
        while(current != null) {
            Visit(current);
            if(current.left != null) {
                q.add(current.left);
            }
            if(current.right != null) {
                q.add(current.right);
            }
            if(q.isEmpty()) return ;
            current = q.remove(0);
        }
    }

以上就是四种基本遍历方式。下面我们来测试一下，首先写一个工具函数，用来显示当前节点的值。

    //*********辅助工具****************
    public void Visit(TreeNode node) {
        System.out.print(node.val);
    }

写Test测试函数：

　　

    @Test
    public void fun() {
        TreeNode root = new TreeNode('+');
        root.left = new TreeNode('-');
        root.right = new TreeNode('E');
        root.left.left = new TreeNode('*');
        root.left.right = new TreeNode('D');
        root.left.left.left = new TreeNode('/');
        root.left.left.right = new TreeNode('C');
        root.left.left.left.left = new TreeNode('A');
        root.left.left.left.right = new TreeNode('B');

        System.out.println("中序遍历：");
        InOrder(root);
        System.out.println();
        System.out.println("前序遍历：");
        PreOrder(root);
        System.out.println();
        System.out.println("后序遍历：");
        PostOrder(root);
        System.out.println();
        System.out.println("层序遍历：");
        LevelOrder(root);
        System.out.println();
    }

由上面的测试函数得到遍历结果：

全部代码：

package tree;

import java.util.ArrayList;
import java.util.List;

import org.junit.Test;
/**
 * 二叉数的遍历
 *                     +
 *                 -         E
 *             *        D
 *        /        C
 *   A        B
 * @author Ranter
 *
 */
public class BinaryTree {
    @Test
    public void fun() {
        TreeNode root = new TreeNode('+');
        root.left = new TreeNode('-');
        root.right = new TreeNode('E');
        root.left.left = new TreeNode('*');
        root.left.right = new TreeNode('D');
        root.left.left.left = new TreeNode('/');
        root.left.left.right = new TreeNode('C');
        root.left.left.left.left = new TreeNode('A');
        root.left.left.left.right = new TreeNode('B');

        System.out.println("中序遍历：");
        InOrder(root);
        System.out.println();
        System.out.println("前序遍历：");
        PreOrder(root);
        System.out.println();
        System.out.println("后序遍历：");
        PostOrder(root);
        System.out.println();
        System.out.println("层序遍历：");
        LevelOrder(root);
        System.out.println();
    }

    //****************************************************************

    //中序遍历        左-根-右    （前中后：根的位置）
    public void InOrder(TreeNode current){
        if(current != null) {
            InOrder(current.left);
            Visit(current);
            InOrder(current.right);
        }
    }
    //前序遍历        根-左-右
    public void PreOrder(TreeNode current){
        if(current != null) {
            Visit(current);
            InOrder(current.left);
            InOrder(current.right);
        }
    }
    //后续遍历        左-右-根
    public void PostOrder(TreeNode current){
        if(current != null) {
            InOrder(current.left);
            InOrder(current.right);
            Visit(current);
        }
    }
    //层序遍历        同一层节点从左往右依次遍历(使用队列层序遍历)
    public void LevelOrder(TreeNode current){
        List<TreeNode> q = new ArrayList<TreeNode>();
        while(current != null) {
            Visit(current);
            if(current.left != null) {
                q.add(current.left);
            }
            if(current.right != null) {
                q.add(current.right);
            }
            if(q.isEmpty()) return ;
            current = q.remove(0);
        }
    }

    //*********辅助工具****************
    public void Visit(TreeNode node) {
        System.out.print(node.val);
    }

    //树节点
    class TreeNode {
        public char val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(char x) {
            val = x;
        }
    }
}