CMU Database Systems - Indexes

这章主要描述索引，即通过什么样的数据结构可以更加快速的查询到数据

介绍Hash Tables，B+tree，SkipList

以及索引的并行访问

Hash Tables

hash tables可以实现O(1)的查询，设计主要考虑两点

首先用什么hash function？底下列出常用的hash function

然后怎么解决collisions？即hash schemes

首先是static hash schemes

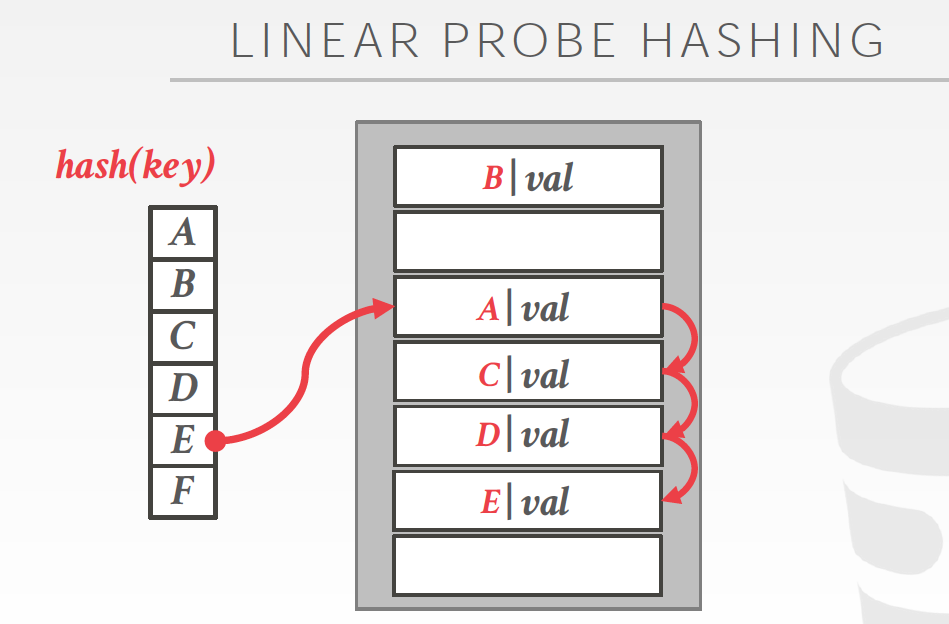
第一个方法是Linear probe hashing

方法，如果发现冲突，就往后找，直到找到一个free的slot，所以要同时记录下key和value，这样才好去比对每个key是不是要找的

问题如图，会出现bad case，比如对于E，需要跳很多步才能找到，这样查询就从O(1)变成O(n)了

Robin Hood Hashing

像名字一样，罗宾汉，劫富济贫，解决badcase

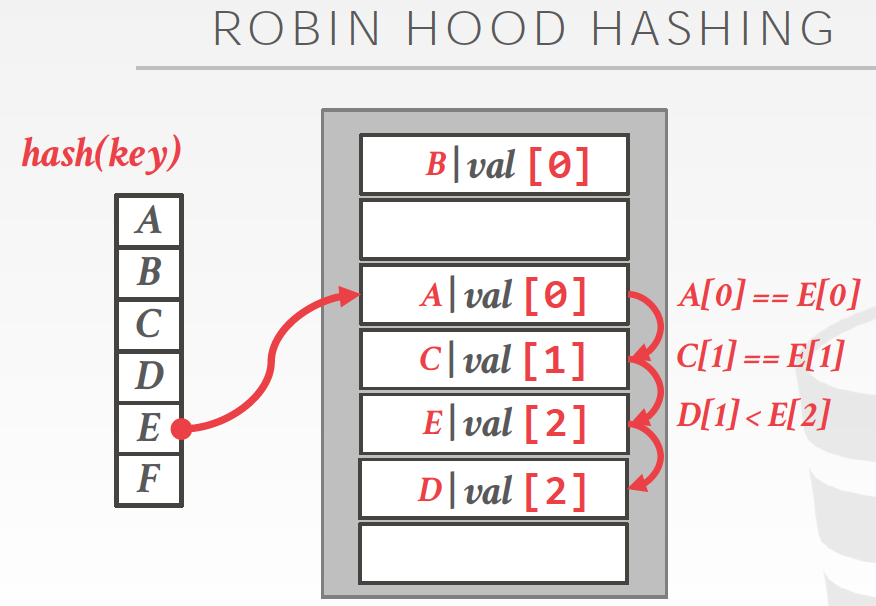
首先存储到时候，要加上跳数，jump几次；然后根据jump数比较，来判断是否要做平均

左图，如果不用robin hood方式，D为1跳，E为3跳

右图，用robin hood后，D和E都变成2跳

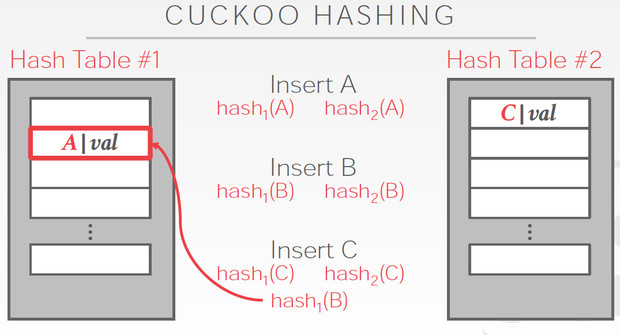
Cuckoo Hashing

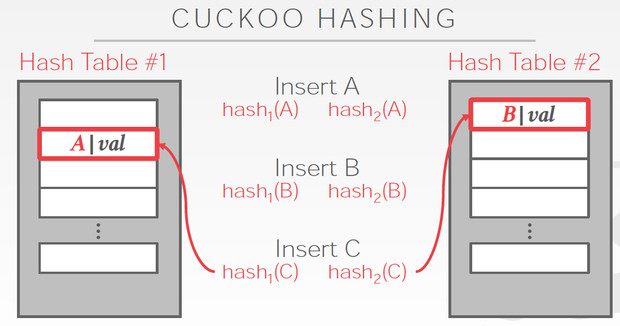
简单的说，用多个hash table，对于一个数据，哪边空就存哪边

但是对于当前这个C，两边都冲突，他解决的思路是，

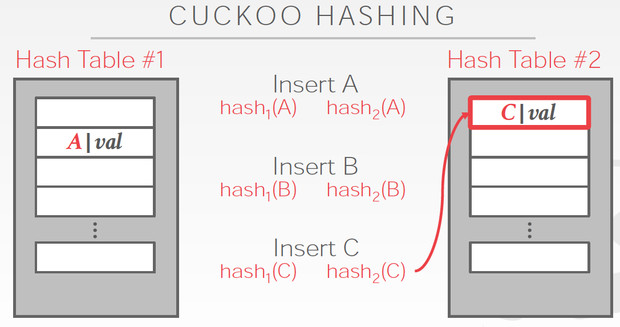
C两边都冲突那肯定是解不了，那我先把C随便存一边，这样如图，我们就要解决B的冲突

B只能去替换A，最终A可以存在另一张表里面，所以冲突解决

这个方法明显的好处是查询路径短，最多两次

问题是，插入性能容易比较差，如果冲突比较多，有可能死循环，所以如果出现这些情况，就要去降低冲突率，比如增加hash table的大小，或者增加hashtable的个数

但这样变化后，需要完全重新rebuild

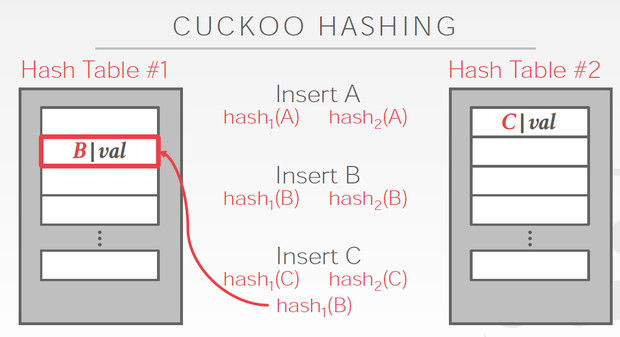
static hash schemes的问题就是，容量有限，一旦超出扩容的话，就需要整个索引完全rebuild

所以就需要Dynamic hash table

最直白的想法是Chained Hashing，hash值对应的是buckets，不存在collision，因为buckets是可以无限扩展的

问题是，数据多了，就变成O(n)了

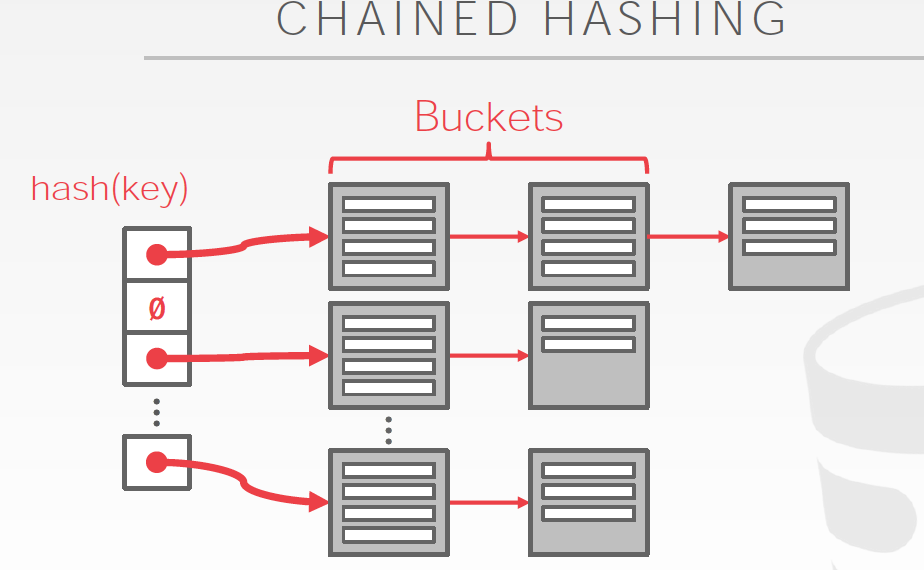
上面的方法的问题是，随着数据的增多不断的增加bucket，但是没有没有增加目录大小，最终对应到目录中一条的数据越来越多，失去了index的意义

Extendible hashing

这个方法难理解些，

首先这里的hash函数是根据前几位去分bucket，depth的意思是几位

比如，用2位分bucket，目录大小为4，不够了就用3位去分bucket，目录大小就是8

Global depth是目录用几位，local depth其实只是个标识，表示这个bucket用的是几位，

因为只要有一个分区的bucket满了，并且如果这个分区只对应一个目录item，那么目录就需要扩展，global depth会增加

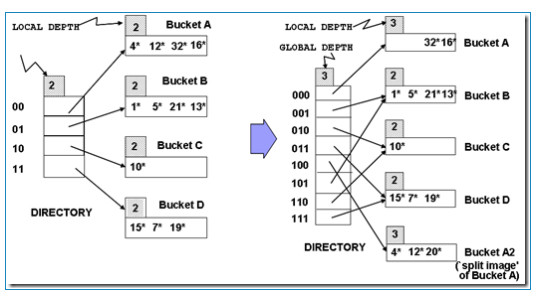
比如下图中，00指向bucketA，已经4个数满了，还要加一个，只有分离bucket，这个时候就需要扩展目录，global depth=3，其中000，001分别指向一个bucket

但是其他的bucket没满啊，所以他们的local depth还是2，并且在新的目录中，有两个item指向depth为2的bucket

但这时来个9，落在bucketB，B也满了，需要分裂，但是这个时候就不需要扩展目录，因为B本身就有两个目录item指向，正好可以分开

Linear Hashing

这个的思路也是逐步的分裂bucket，但他和extendible hashing相比，不需要维护这个目录

http://queper.in/drupal/blogs/dbsys/linear_hashing，这个链接里面的例子非常清楚

基本思想，

初始bucket数是4，按4取模分bucket，很容易理解
问题是，如果有某个bucket满了，怎么处理？

首先把overflow的数据用一个临时bucket存下来

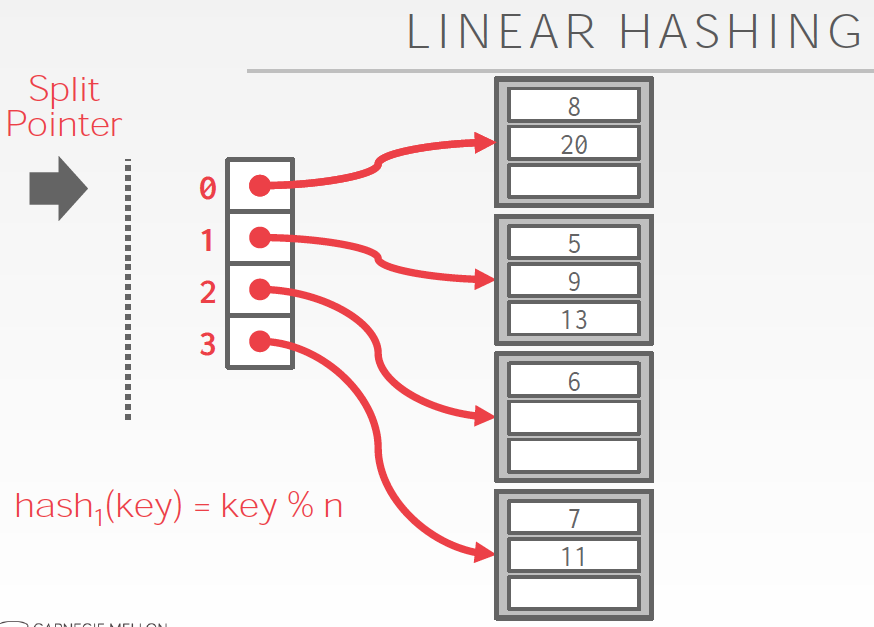
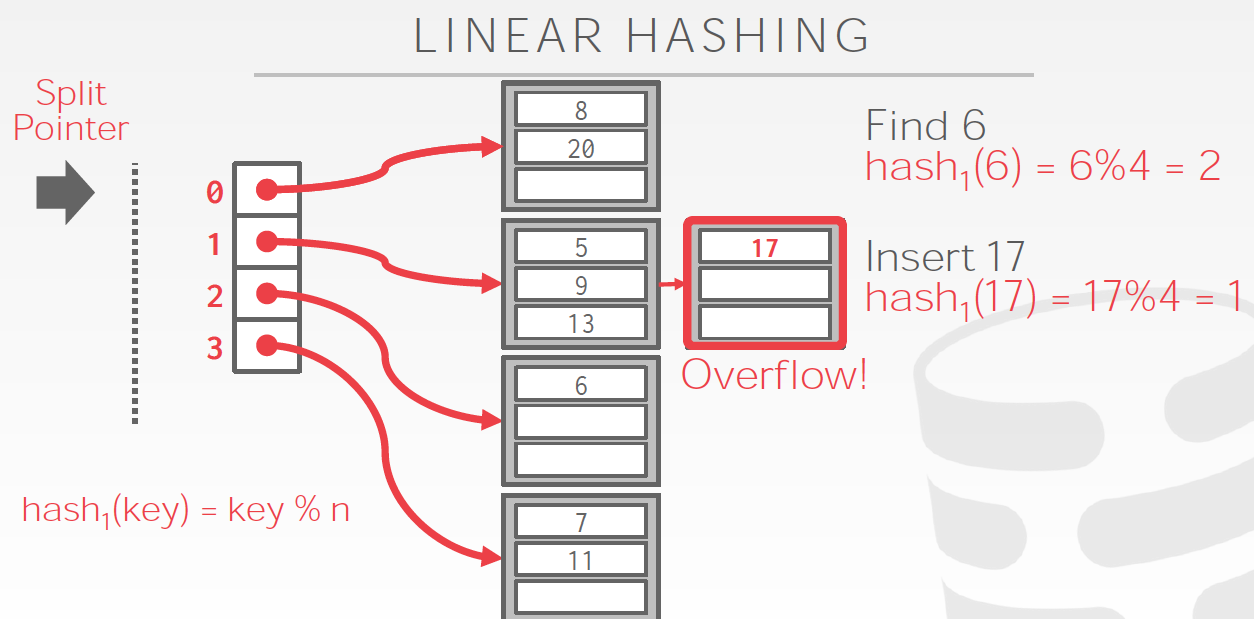
然后接着要做bucket分裂，

这里bucket分裂的过程比较trick是逐步完成的，最终达到的是bucket翻倍

因为要一个个bucket分裂，所以这里有个split point，表示当前分裂到哪个bucket了

这里很难理解的是，他不是分裂overflow的那个bucket，而且按顺序一个个分裂；感觉一次把所有bucket全split掉，也没啥问题

如图，bucket 1 满了，但他是分裂当前split point指向的bucket 0，分成0和4，并且split point + 1

分裂的时候用的hash函数是下一轮的函数，如图的hash2

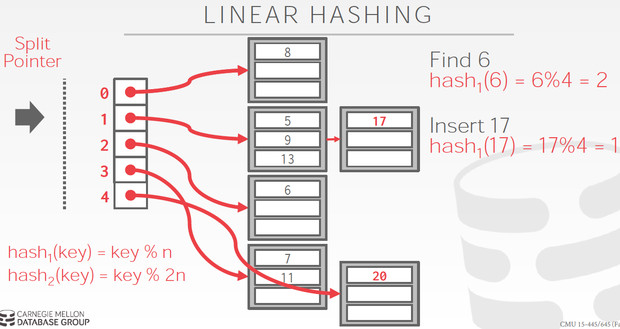
这里每overflow一次，就按顺序分裂一个bucket，当split point为4的时候，即分裂完一轮了，当前bucket=8

把split point重置成0，开始下一轮，每轮的bucket数翻倍，所以hash函数中的取余的数也要翻倍，很容易理解

这样就实现了动态扩展

Tree Indexes

https://www.cnblogs.com/fxjwind/archive/2012/06/09/2543357.html

我们说的B tree，往往说的都是B+ tree；B-tree和B+tree的区别就在于inner node是否存储数据

B+树有如下的特性，

m叉而非二叉，可以有效降低树高

每个inner node至少是half-full，这样提高读取效率，读取一个节点，往往是一个page，可以读取尽可能多的数据

inner node，对于k个keys，要有k+1个非null子节点

B+数据的结构如下，

分为inner nodes和leaf nodes

inner nodes只有索引，而leaf nodes包含真实数据，而且还有sibling pointers，这是为了更有效的range 查询

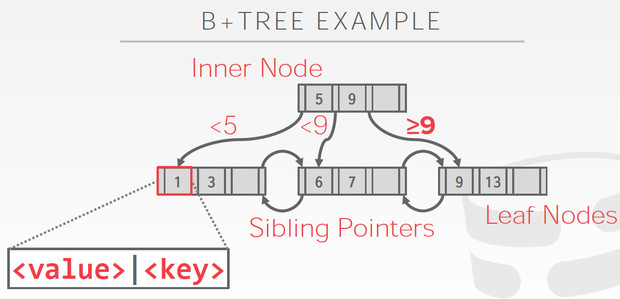
Leaf node的内容也分为两种

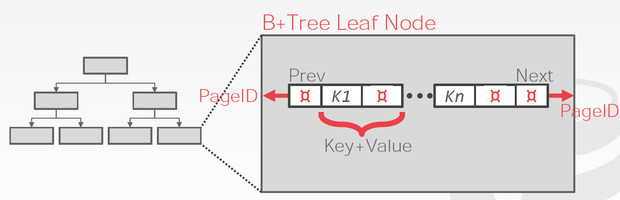
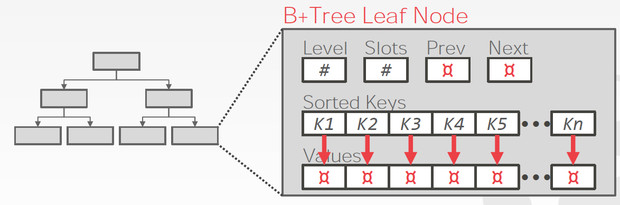
Leaf Node的结构如下，

两种kv不同的存储格式，这里pageId，需要理解一下，因为往往B+数的一个节点对应于一个page，所以跳到下一个节点，就是跳到另一个page

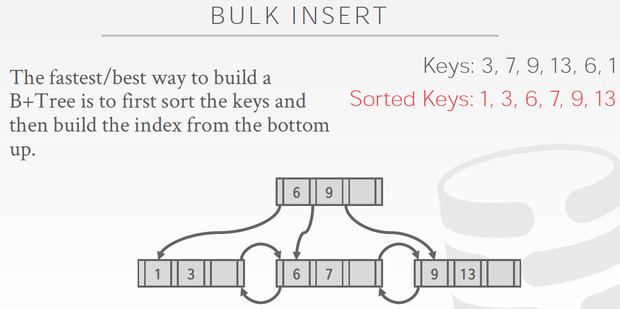
B+树的insert和delete，

Insert，关键就是node满了，需要分裂，分裂完要把middle key放到上一层节点中做索引，如果上一层节点也满了，就需要进一步分裂

delete，关键是如果delete后，节点小于half-full，需要先试图从sibling去借一些达到，half-full，如果sibling也达不到half-full，那么就merge

Clustered Indexes

http://baijiahao.baidu.com/s?id=1598257553176708891&wfr=spider&for=pc

clustered indexes是B+树的应用，

在Innodb里面，每个表都有一个聚簇索引，该索引是根据primary key对行记录生成的B+树索引，如果没有primary key，会生成自增id作为替代；

叶子节点存放的是行数据，称之为数据页，故表中的数据也是聚簇索引中的一部分，数据页之间通过一个双向链表来链接

除了Clustered Indexes以外，都称为Secondary Indexes，与聚簇索引的区别在于辅助索引的叶子节点中存放的是主键的键值

Clustered indexes只有一个，但是辅助索引却可以有多个

可想而知，通过辅助索引只能查到主键id，所以如果你要读到数据，还要再查一次聚簇索引；好处是因为辅助索引不包含数据，所以远小于聚簇索引，查询效率比较高

可以用一列，也可以用多列来创建辅助索引，称为联合索引，
联合索引和普通索引的结构没有不同，只是会在节点中同时记录下多个列的值，遵循最左原则，就是先按第一个列排序，再按第二个列排序。。。。。。

所以查询条件，也需要满足最左原则，否则无法使用索引

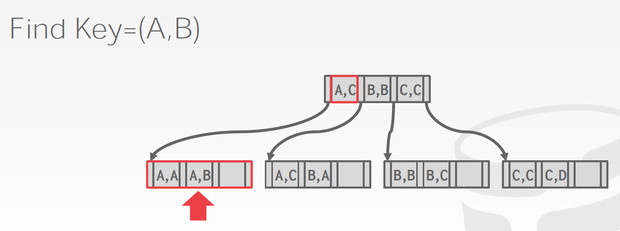
对于变长的keys和重复的keys

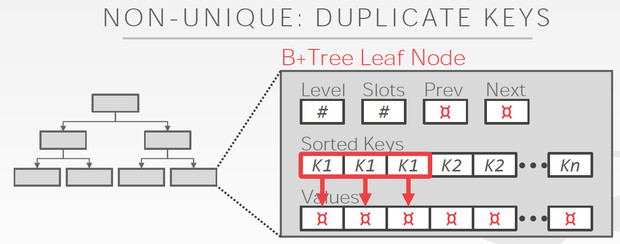
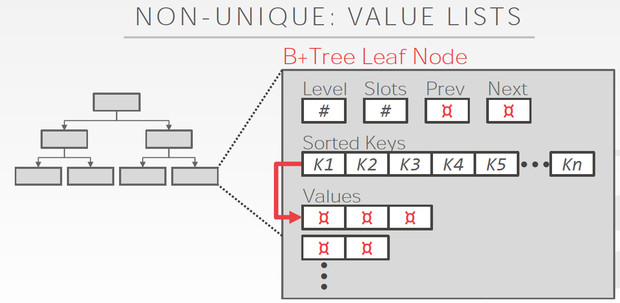
节点内的search方法，

其他B+树还有些优化，

索引覆盖，CoveringIndexes

查询需要的数据，都可以在索引中获取到，不需要读取原始tuple

SkipList，跳表

http://www.cnblogs.com/seniusen/p/9870398.html

如果用有序的数组来实现索引，可以简单的用二分查找，但是插入和删除数据会比较麻烦；

最简单的方法实现动态保序的index的方法是用有序链表，但链表的只支持线性搜索，时间复杂度为O(n)

如何让链表也能二分查找，提高查询效率，这就是skiplist

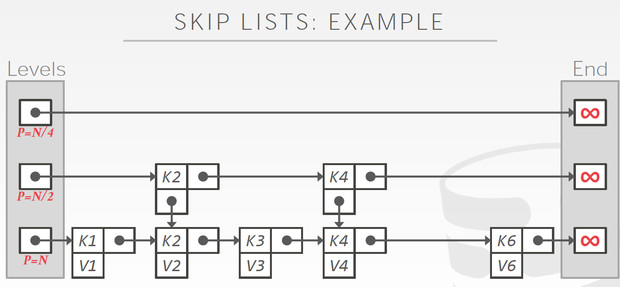
跳表的数据存在第一层，上面的都是索引，想法很简单，避免一个个遍历，越往上层建的索引越稀疏，总之就是为了模拟出二分查找，空间换时间，所以时间复杂度可以近似O(logn)

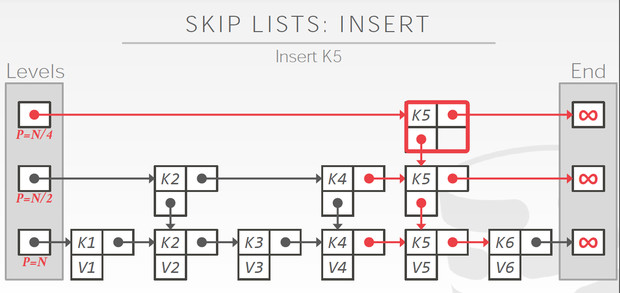
跳表比较有意思的是他的insert过程，

比如插入，k5v5，这里关键是如何建立索引？即要把K5加到哪几层里面

这里的答案是flip coin，就是一个伯努利过程

连续抛硬币，连续出现正面的次数为k，我们就会对前k层建立索引

如果k大于当前最大的level，就需要创建新的level

这有两个好处，

因为是伯努利过程，所以自然约高的level出现概率越低，以1/2降低

并且插入的数据越多，出现较大k的概率越大，因为较大的k是小概率事件

这个设计的还是非常精巧的，和loglogcounting类似的思路

跳表的查询就比较直观了，二分查找下来就ok

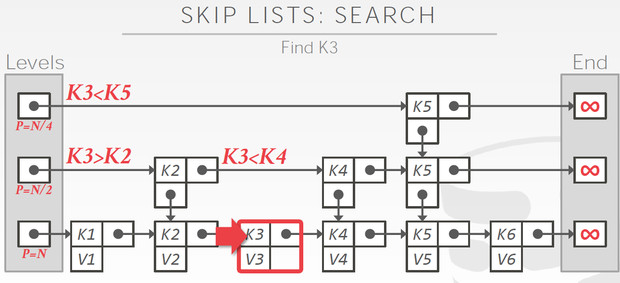
跳表的删除，也不难理解，关键是需要一个标识，先逻辑删除，再物理删除

图中就是刚完成逻辑删除，物理删除就是把这些节点真正删掉

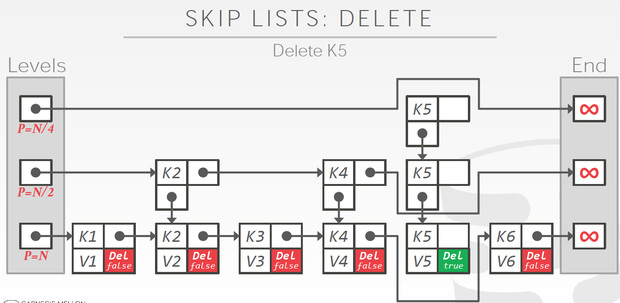
跳表的优缺点

Radix Tree

核心的思路，前缀树，节点的path就代表key，可以reconstructed

树高，取决于key的length，而不是key的多少；其实key多了，表示key的length肯定要变长，一样的

不需要rebalance

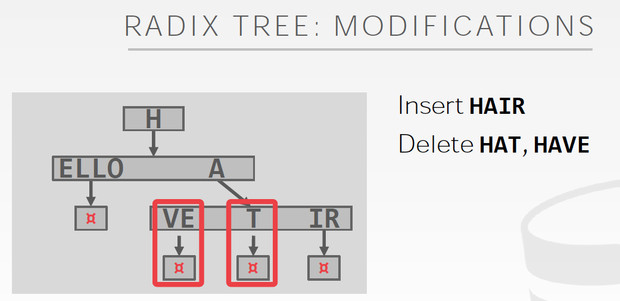
Radix Tree的例子，看出和Trie的区别

Radix只有共享的才需要单独的节点

Radix的优点，就是插入和删除特别简单

Index Concurrency Control

讨论多线程并发访问索引
其中Logical correctness是指应用层的，transaction
而这里主要讨论的是Physical correctness，内部数据结构的并发访问

这里再解释在数据库领域，lock和latch的区别

既然讨论的是内部数据结构的并发控制，那用的就是latch

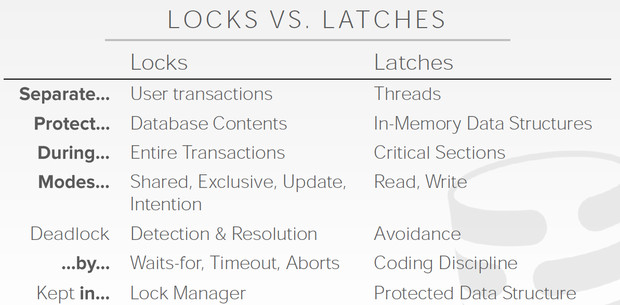
Latch分为两种类型，读和写

从表中可以看出来，我们要解决写写，和读写冲突，读读是没有冲突的

对于数据库中主要的索引结构，B+tree

解决冲突的方式称为，Latch Crabbing/Coupling

这个其实很容易理解，

读比较简单，从root开始，只要能获取到child的latch，就可以释放parent

更新复杂些，因为我更新当前节点，可能会导致split和merge，这样父节点也需要更新
所以要同时获取父子两层的latch，只有当不会发生split和merge，所以没有必要改动父节点，safe，才释放父节点的latch

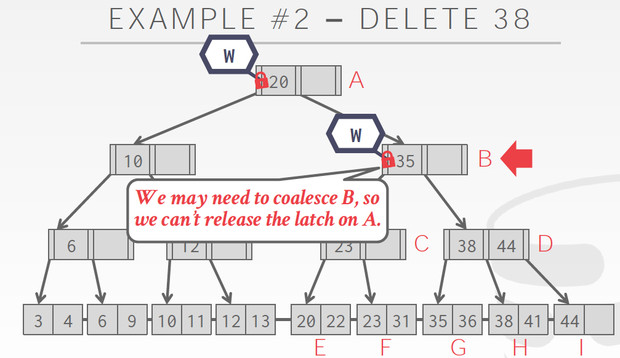
Delete的例子，对于delete我们要考虑的是否要merge

所以在B的时候，我们不能释放A的Latch，因为B只有一个35，可能在delete的过程中需要merge
而到了C，C有38，44，删除一个也不会导致merge，所以可以释放A，B的latch

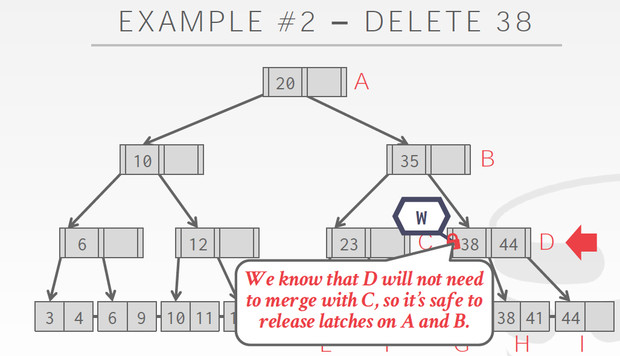
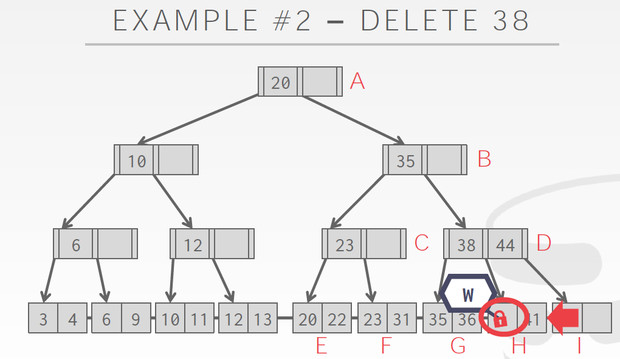
同样对于Insert，我们要考虑的是split
B的时候，有一个空，没有split的风险，释放A
但到D的时候，有split的风险，不能释放B，到I发现有空，不需要split，释放B，D

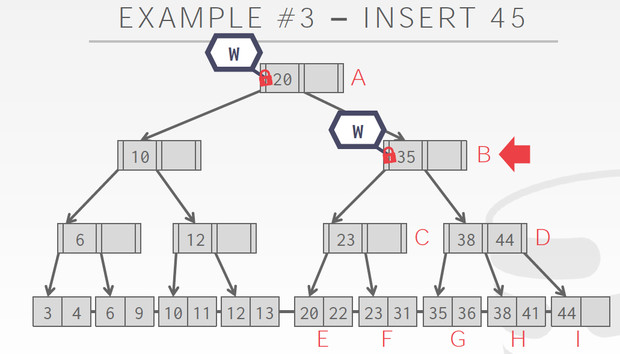
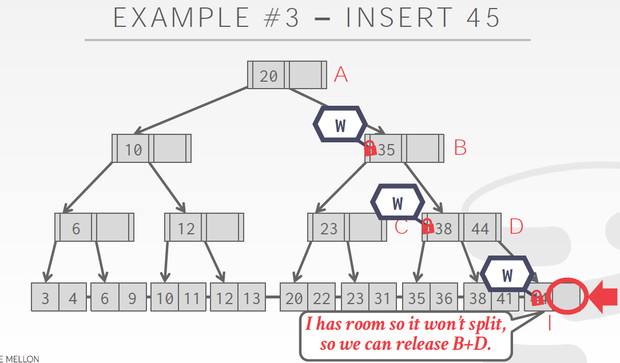
这个Case到F的时候，发现要split，所以不能释放C的latch，C也要增加节点

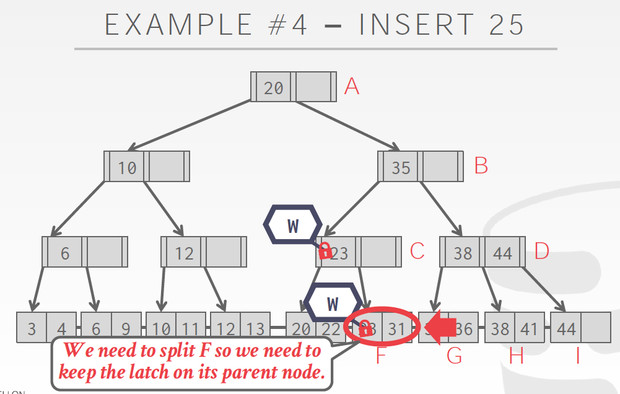
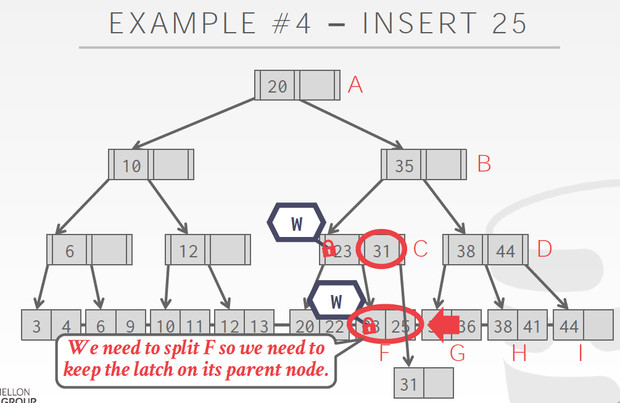
这个方法有个显著的问题，

Root会成为明显的瓶颈，以为所有锁都要从root开始锁起

优化的思路，

这有个假设，就是大部分更新是不需要，split和merge的，否则效率反而更低了

如果不需要split和merge，就没有必要给parent加写latch，用读latch就可以；用读latch，首先避免每次都在root写写冲突，因为读读是不冲突的，而且又保证了读写冲突，因为别人在更新的同时，你需要等待的

Leaf Node Scan

前面说的latch的方式都是Top-down的，所以不会产生死锁，大家加锁的方向一致的，不会形成环

但是B+tree在leaf node之间也是有pointer的，这就会形成环

读的场景，不冲突

写的场景，就会产生冲突

T2，冲突的时候，有两个选择，一个是等，一个是自杀(防止死锁)
因为T2不知道T1在干啥，所以合理的方式是，等一个timeout，然后自杀，这样可以有效避免死锁

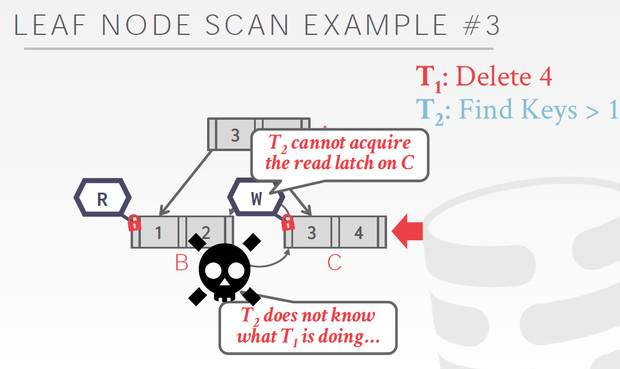
Delayed parent updates

延迟对于parent的变更，这样会更有效

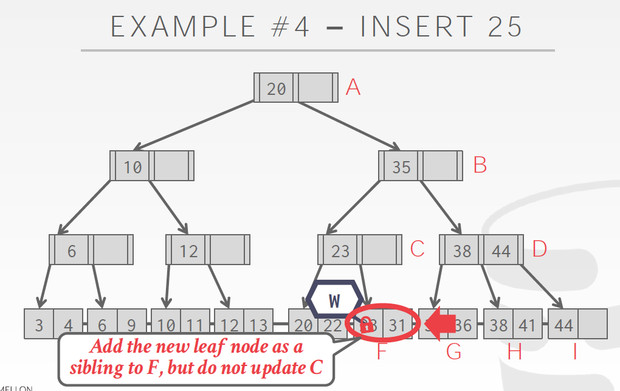
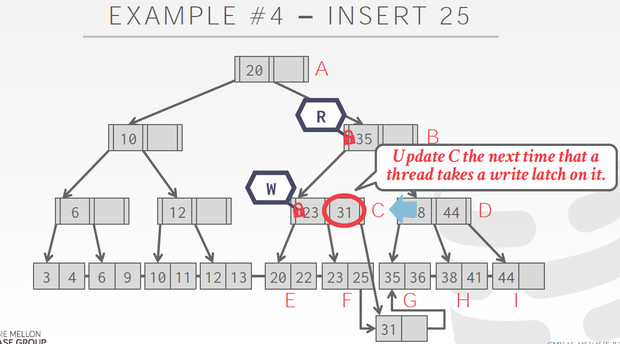
后续会有线程单独的来更新parent

对于parent的更新可以批量，并且降低写latch的冲突的概率