洛谷 P3398 仓鼠找sugar 题解

每日一题 day44 打卡

Analysis

首先有一个结论：先找 p1=(a,b),p2=(c,d) 的LCA的深度，在与(a,c),(a,d),(b,c),(b,d)中最深的LCA n的深度比较，如果 n <=p1 & n<=p2 说明两条路径相交（即满足题目要求）。

假设 (b,c) 是最深的LCA n,  p1=dep[LCA(a,b)] .

且 n>=p1.

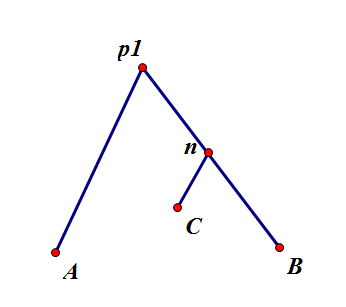
因为是树，所以每个点走到其LCA的路径只有一条。

也就是说，n点在b到p1的路径上，即两条路径相交

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define int long long
 #define maxn 100000+10
 #define rep(i,s,e) for(register int i=s;i<=e;++i)
 #define dwn(i,s,e) for(register int i=s;i>=e;--i)
 using namespace std;
 inline int read()
 {
     int x=,f=;
     char c=getchar();
     while(c<''||c>'') {if(c=='-') f=-; c=getchar();}
     while(c>=''&&c<='') {x=x*+c-''; c=getchar();}
     return f*x;
 }
 inline void write(int x)
 {
     if(x<) {putchar('-'); x=-x;}
     if(x>) write(x/);
     putchar(x%+'');
 }
 int n,q,cnt;
 int dep[maxn],dp[maxn][+];
 int head[*maxn];
 struct node
 {
     int v,nex;
 }edge[*maxn];
 inline int max_four(int a1,int a2,int a3,int a4)
 {
     return max(max(a1,a2),max(a3,a4));
 }
 inline void add(int x,int y)
 {
     edge[++cnt].v=y;
     edge[cnt].nex=head[x];
     head[x]=cnt;
 }
 void init(int from,int father)
 {
     dep[from]=dep[father]+;
     rep(i,,) dp[from][i]=dp[dp[from][i-]][i-];
     for(int i=head[from];i;i=edge[i].nex)
     {
         int to=edge[i].v;
         if(to==father) continue;
         dp[to][]=from;
         init(to,from);
     }
 }
 int LCA(int x,int y)
 {
     if(dep[x]<dep[y]) swap(x,y);
     dwn(i,,)
     {
         if(dep[dp[x][i]]>=dep[y])
             x=dp[x][i];
         if(x==y) return x;
     }
     dwn(i,,)
     {
         if(dp[x][i]!=dp[y][i])
         {
             x=dp[x][i];
             y=dp[y][i];
         }
     }
     return dp[x][];
 }
 signed main()
 {
     n=read();q=read();
     rep(i,,n-)
     {
         int x=read(),y=read();
         add(x,y);
         add(y,x);
     }
     init(,);
     rep(i,,q)
     {
         int a=read(),b=read(),c=read(),d=read();
         int p1=dep[LCA(a,b)],p2=dep[LCA(c,d)];
         int n1=LCA(a,c),n2=LCA(a,d),n3=LCA(b,c),n4=LCA(b,d);
         int com=max_four(dep[n1],dep[n2],dep[n3],dep[n4]);
         if(p1<=com&&p2<=com) printf("Y\n");
         else printf("N\n");
     }
     return ;
 }

请各位大佬斧正（反正我不认识斧正是什么意思）