torch_03_二分类

logistic回归

博客链接：https://www.cnblogs.com/home123/p/7356523.html

分类器：监督学习从数据中学习一个分类模型或者分类决策函数，被称为分类器（classification）
分类；二分类，多分类
发生的几率：指该事件发生的概率与不发生的概率的比值
eg：一个事件发生的概率为p，发生的几率是p/(1-p)
对数几率：logit（p） = log p/(1-p)

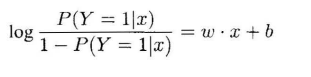
note：p(y = 1|x) = 1-p(y=0|x)

在logistic回归的模型中，输出Y=1 的对数几率是输入x的线性函数。另外，线性函数的值越接近正无穷，概率值就越接近1；线性函数的值越接近负无穷，概率值越接近0.

模型的参数估计：