机器学习算法--svm实战
1、不平衡数据分类问题
对于非平衡级分类超平面,使用不平衡SVC找出最优分类超平面,基本的思想是,我们先找到一个普通的分类超平面,自动进行校正,求出最优的分类超平面
测试代码如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
rng = np.random.RandomState(0)
n_samples_1 = 1000
n_samples_2 = 100
X = np.r_[1.5 * rng.randn(n_samples_1, 2),0.5 * rng.randn(n_samples_2, 2) + [2, 2]]
y = [0] * (n_samples_1) + [1] * (n_samples_2)
print X
print y clf = svm.SVC(kernel='linear', C=1.0)
clf.fit(X, y)
w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-5, 5)
yy = a * xx - clf.intercept_[0] / w[1]
wclf = svm.SVC(kernel='linear', class_weight={1: 10})
wclf.fit(X, y) ww = wclf.coef_[0]
wa = -ww[0] / ww[1]
wyy = wa * xx - wclf.intercept_[0] / ww[1] h0 = plt.plot(xx, yy, 'k-', label='no weights')
h1 = plt.plot(xx, wyy, 'k--', label='with weights')
plt.scatter(X[:, 0], X[:, 1], c=y)
plt.legend() plt.axis('tight')
plt.show()
运行结果如下:
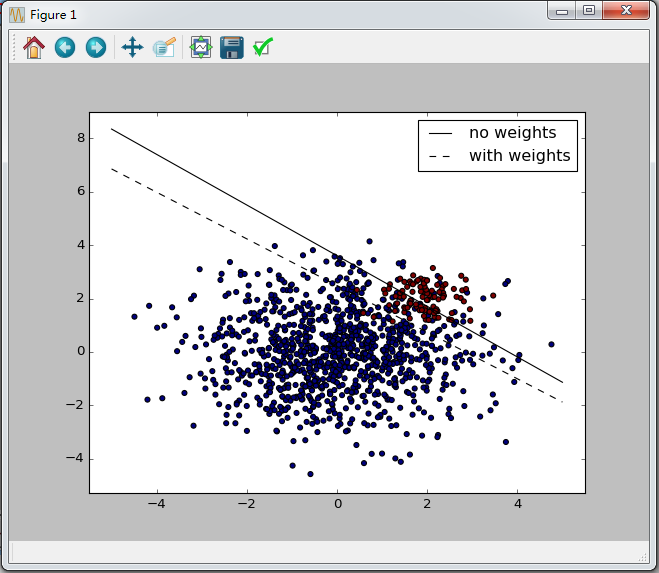
2、回归问题
import numpy as np
from sklearn.svm import SVR
import matplotlib.pyplot as plt X = np.sort(5 * np.random.rand(40, 1), axis=0)
y = np.sin(X).ravel() y[::5] += 3 * (0.5 - np.random.rand(8)) svr_rbf = SVR(kernel='rbf', C=1e3, gamma=0.1)
svr_lin = SVR(kernel='linear', C=1e3)
svr_poly = SVR(kernel='poly', C=1e3, degree=2)
y_rbf = svr_rbf.fit(X, y).predict(X)
y_lin = svr_lin.fit(X, y).predict(X)
y_poly = svr_poly.fit(X, y).predict(X) lw = 2
plt.scatter(X, y, color='darkorange', label='data')
plt.hold('on')
plt.plot(X, y_rbf, color='navy', lw=lw, label='RBF model')
plt.plot(X, y_lin, color='c', lw=lw, label='Linear model')
plt.plot(X, y_poly, color='cornflowerblue', lw=lw, label='Polynomial model')
plt.xlabel('data')
plt.ylabel('target')
plt.title('Support Vector Regression')
plt.legend()
plt.show()
运行结果如下:
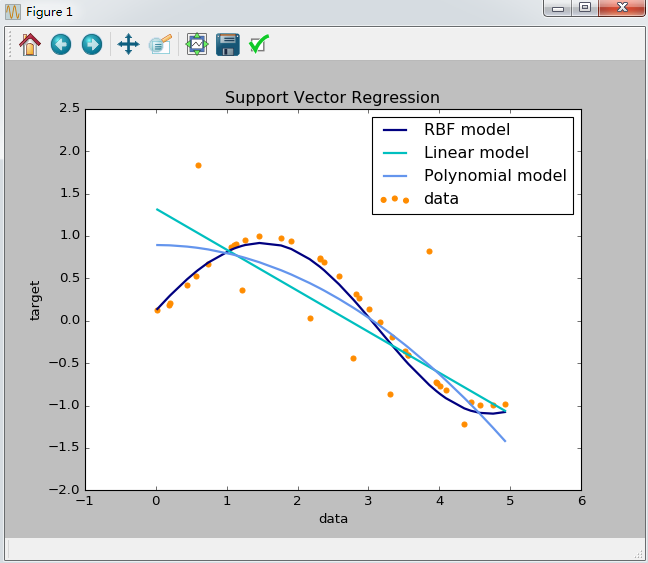
机器学习算法--svm实战的更多相关文章
- 【机器学习算法基础+实战系列】SVM
概述 支持向量机是一种二分类模型,间隔最大使它有别于感知机.支持向量机学习方法由简至繁的模型:线性可分支持向量机(linear support vector machine in linearly s ...
- 数学之路(3)-机器学习(3)-机器学习算法-SVM[7]
SVM是新近出现的强大的数据挖掘工具,它在文本分类.手写文字识别.图像分类.生物序列分析等实际应用中表现出非常好的性能.SVM属于监督学习算法,样本以属性向量的形式提供,所以输入空间是Rn的子集. 图 ...
- 机器学习算法 --- SVM (Support Vector Machine)
一.SVM的简介 SVM(Support Vector Machine,中文名:支持向量机),是一种非常常用的机器学习分类算法,也是在传统机器学习(在以神经网络为主的深度学习出现以前)中一种非常牛X的 ...
- 机器学习 - 算法 - SVM 支持向量机
SVM 原理引入 支持向量机( SVM,Support Vector Machine ) 背景 2012年前较为火热, 但是在12年后被神经网络逼宫, 由于应用场景以及应用算法的不同, SVM还是需要 ...
- 数学之路(3)-机器学习(3)-机器学习算法-SVM[5]
svm小结 1.超平面 两种颜色的点分别代表两个类别,红颜色的线表示一个可行的超平面.在进行分类的时候,我们将数据点 x 代入 f(x) 中,如果得到的结果小于 0 ,则赋予其类别 -1 ,如果 ...
- 数学之路(3)-机器学习(3)-机器学习算法-SVM[9]
我们应用SVM的非线性分类功能对手写数字进行识别,我们在这应用poly做为非线性核 svm = mlpy.LibSvm(svm_type='c_svc', kernel_type='poly',gam ...
- 【机器学习算法基础+实战系列】KNN算法
k 近邻法(K-nearest neighbor)是一种基本的分类方法 基本思路: 给定一个训练数据集,对于新的输入实例,在训练数据集中找到与该实例最邻近的k个实例,这k个实例多数属于某个类别,就把输 ...
- 机器学习 - 算法 - SVM 支持向量机 Py 实现 / 人脸识别案例
SVM 代码实现展示 相关模块引入 %matplotlib inline import numpy as np import matplotlib.pyplot as plt from scipy i ...
- 【机器学习】svm
机器学习算法--SVM 目录 机器学习算法--SVM 1. 背景 2. SVM推导 2.1 几何间隔和函数间隔 2.2 SVM原问题 2.3 SVM对偶问题 2.4 SMO算法 2.4.1 更新公式 ...
随机推荐
- rac数据库单连接报错ora-12537解决办法
1.现象如下: C:\Users\Administrator.DBA-PC>sqlplus sys/oracle@192.168.100.33:1521/orcl as sys dba SQL* ...
- linux设备驱动开发详解 笔记
在目录的 Makefile 中关于 RTC_DRV_S3C 的编译脚本为: obj -$(CONFIG_RTC_DRV_S3C) += rtc-s3c.o 上述脚本意味着如果 RTC_DRV_S3 ...
- Python爬虫框架Scrapy实例(一)
目标任务:爬取腾讯社招信息,需要爬取的内容为:职位名称,职位的详情链接,职位类别,招聘人数,工作地点,发布时间. 一.创建Scrapy项目 scrapy startproject Tencent 命令 ...
- Django - rest - framework - 下
一.视图三部曲 https://www.cnblogs.com/wupeiqi/articles/7805382.html 使用混合(mixins) 之前得视图部分 # urls.py from dj ...
- loadNibNamed:(NSString *)name owner:(nullable id)owner options:(nullable NSDictionary *)options用法
1.name xib的名字 owner当前类对象 options初始参数 实际应用: NSArray *nibs = [[NSBundle mainBundle] loadNibNamed:@&quo ...
- nodejs Async详解之二:工具类
Async中提供了几个工具类,给我们提供一些小便利: memoize unmemoize log dir noConflict 1. memoize(fn, [hasher]) 有一些方法比较耗时,且 ...
- Miller-Rabin素数测试算法(POJ1811Prime Test)
题目链接:http://poj.org/problem?id=1811 题目解析:2<=n<2^54,如果n是素数直接输出,否则求N的最小质因数. 求大整数最小质因数的算法没看懂,不打算看 ...
- Selenium之Chrome浏览器的启动问题及解决
System.setProperty("webdriver.chrome.driver","chromedriver.exe路径"); 配置好Chrome的驱动 ...
- python3 os.walk()使用
os.walk() 方法用于通过在目录树种游走输出在目录中的文件名,向上或者向下. 在Unix,Windows中有效. os.walk(top[, topdown=True[, onerror=Non ...
- Qt emit的使用
1. 假设现在我定义了一个类A,现在想在A的一个函数void A::function1()当中的结尾处emit一个信号signal1(),然后利用这个信号触发另一个类B进行某项操作void B::fu ...
