K:汉诺塔问题
相关介绍:
汉诺塔问题是一个通过隐式使用递归栈来进行实现的一个经典问题,该问题最早的发明人是法国数学家爱德华·卢卡斯。传说印度某间寺院有三根柱子,上串64个金盘。寺院里的僧侣依照一个古老的预言,以上述规则移动这些盘子;预言说当这些盘子移动完毕,世界就会灭亡。这个传说叫做梵天寺之塔问题(Tower of Brahma puzzle)。但不知道是卢卡斯自创的这个传说,还是他受他人启发。若传说属实,僧侣们需要2^64 − 1步才能完成这个任务;若他们每秒可完成一个盘子的移动,就需要5845亿年才能完成。整个宇宙现在也不过137亿年。这个传说有若干变体:寺院换成修道院、僧侣换成修士等等。寺院的地点众说纷纭,其中一说是位于越南的河内,所以被命名为“河内塔”。另外亦有“金盘是创世时所造”、“僧侣们每天移动一盘”之类的背景设定。佛教中确实有“浮屠”(塔)这种建筑;有些浮屠亦遵守上述规则而建。“汉诺塔”一名可能是由中南半岛在殖民时期传入欧洲的。
其问题的形式化描述如下:假设有3个分别命名为X,Y,Z的塔座,在塔座X上插有n个直径大小各不相同,且从小到大编号为1、2、......、n的圆盘。现要求将塔座X上的n个圆盘借助塔座Y移至塔座Z上,并仍按同样顺序叠排。圆盘移动时必须遵守以下的规则:
- 每次只能移动一个圆盘
- 圆盘可以插在X、Y和Z中的任意一个塔座上
- 任何时刻都不能将一个较大的圆盘压在较小的圆盘之上。
问题分析:
当n=1时,问题较为简单,只要将编号为1的圆盘从塔座X直接移动到塔座Z上即可;当n>1时,需利用塔座Y作辅助塔座,若能先设法将压在编号为n的圆盘上的n-1个圆盘从塔座X移动到塔座Y上,则可将编号为n的圆盘从塔座X移动至塔座Z上,然后将塔座Y上的n-1个圆盘移至塔座Z上。而如何将n-1个圆盘从一个塔座移动至另一个塔座是一个和原问题具有相同特征属性的问题,只是问题的规模小于1,因此可以用同样的办法进行求解。由此可知,求解n阶汉诺塔问题可以用递归分解的方法来进行。
示例代码如下:
package queueandstack;
/**
* 该类用于解决汉诺塔问题
* @author 学徒
*
*/
public class Hanoi
{
//用于搬动次数的记录
private int c=0;
/**
* 将塔座x上按照直径由小到大且自上而下的编号为1至n的n个圆盘按照规则移到塔座z上,y用作辅助塔座
* @param n 圆盘的数目
* @param x 原塔座
* @param y 辅助塔座
* @param z 目标塔座
*/
public void hanoi(int n,char x,char y,char z)
{
if(n==1)
move(x,1,z);//将编号为1的圆盘从x移动到z
else
{
hanoi(n-1,x,z,y);//将x上编号为1到n-1的圆盘移动到y,z做辅助塔座
move(x,n,z);//将编号为n的圆盘从x移动到z
hanoi(n-1,y,x,z);//将y上编号为1至n-1的圆盘移动到z,x做辅助塔座
}
}
/**
* 用于移动操作
* @param x 原塔座
* @param n 圆盘编号
* @param z 目标塔座
*/
public void move(char x,int n,char z)
{
System.out.println("第"+(++c)+"次移动:"+n+"号圆盘,"+x+"->"+z);
}
public static void main(String[] args)
{
Hanoi n=new Hanoi();
n.hanoi(3, 'x', 'y', 'z');//对圆盘数量为3进行移动
}
}
运行结果:
第1次移动:1号圆盘,x->z
第2次移动:2号圆盘,x->y
第3次移动:1号圆盘,z->y
第4次移动:3号圆盘,x->z
第5次移动:1号圆盘,y->x
第6次移动:2号圆盘,y->z
第7次移动:1号圆盘,x->z
-------------->以上内容大部分来自教材《数据结构》,清华大学出版社
其移动情况的示例图如下:
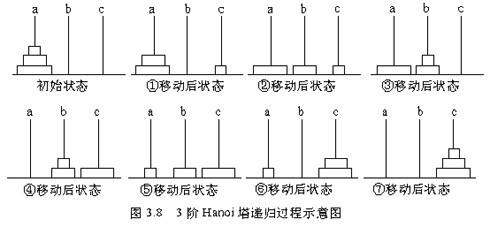
K:汉诺塔问题的更多相关文章
- 数据结构0103汉诺塔&八皇后
主要是从汉诺塔及八皇后问题体会递归算法. 汉诺塔: #include <stdio.h> void move(int n, char x,char y, char z){ if(1==n) ...
- fzu1036四塔问题(汉诺塔问题拓展)
#include<iostream> #include<cstdio> #include<cmath> using namespace std; ]; int ru ...
- codevs3145 汉诺塔问题
难度等级:白银 3145 汉诺塔问题 题目描述 Description 汉诺塔问题(又称为河内塔问题),是一个大家熟知的问题.在A,B,C三根柱子上,有n个不同大小的圆盘(假设半径分别为1-n吧),一 ...
- 新版汉诺塔(UVa10795 - A Different Task)
题目介绍: 标准的汉诺塔上有n个大小各异的盘子.现给定一个初始局面(见图1),求它到目标局面(见图2)至少需要移动多少步? 移动规则:一次只能移动一个盘子:且在移动盘子之前,必须把压在上面的其他盘子先 ...
- Hanio汉诺塔代码递归实现
1.背景介绍 Hanio (汉诺塔,又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘 ...
- 【C语言】汉诺塔问题
之前遇见这个问题,非常费劲地理解了,并写出代码,然后过段时间,再遇见这个问题,又卡住了,如此反反复复两三次,才发现自己对递归的理解依然很肤浅.今天无聊,重温<算法:c语言实现>一书,又遇见 ...
- [CareerCup] 3.4 Towers of Hanoi 汉诺塔
3.4 In the classic problem of the Towers of Hanoi, you have 3 towers and N disks of different sizes ...
- 【BZOJ 1019】【SHOI2008】汉诺塔(待定系数法递推)
1019: [SHOI2008]汉诺塔 Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 559 Solved: 341[Submit][Status] ...
- 【BZOJ】1019: [SHOI2008]汉诺塔
http://www.lydsy.com/JudgeOnline/problem.php?id=1019 题意:汉诺塔规则,只不过盘子n<=30,终点在B柱或C柱,每一次移动要遵守规则:1.小的 ...
随机推荐
- LG的nexus5(32GB版本 - 821)-TOT-底包 可用于救砖!
LG的nexus5(32GB版本 - 821)-TOT-底包 底层修复效果完美,通过LGflashTool1.8直接刷进去就行~ 底包下载: https://pan.baidu.com/s/1Z5WD ...
- 利用Python爬取电影网站
#!/usr/bin/env python #coding = utf-8 ''' 本爬虫是用来爬取6V电影网站上的电影资源的一个小脚本程序,爬取到的电影链接会通过网页的形式显示出来 ''' impo ...
- web环境中的spring MVC
1. web.xml文件的简单详解 在web环境中, spring MVC是建立在IOC容器的基础上,要了解spring mvc,首先要了解Spring IOC容器是如何在web环境中被载入并起作用的 ...
- VS 代码自动对齐快捷键
全部代码代码自动对齐快捷键为 Ctrl + a(按后可松松手) + k(按后可松松手) + f
- jedis 整合 Spring
一, 单机版整合spring 1. 使用默认配置文件进行配置 <bean id="redisClient" class="redis.clients.jedis ...
- SQL1042C running a fenced routine (stored procedure/UDF)
Relation to this link http://www-01.ibm.com/support/docview.wss?uid=swg21399105 2015-01-11-13.38.19. ...
- (转)Db2 备份恢复性能问题诊断与调优
原文:https://www.ibm.com/developerworks/cn/analytics/library/ba-lo-backup-restore-performance-issue-ju ...
- digestmd5.c:4037:15: error: #elif with no expression
执行如下:sed -i.bak 's/#elif WITH_DES/#elif defined(WITH_DES)/' \ plugins/digestmd5.c
- C#(winform)实现不同DPI控件自适应1
1. PicBox控件 顺便一提关键字:stretch [stretʃ] vt. 伸展,张开 //控制pictureBox图片的显示格式 this.picClose.BackgroundImageLa ...
- 查找checked的checkbox和raido
<fieldset id="checkArray"> <input type="checkbox" name="chk[]" ...
