ACM ICPC, Amman Collegiate Programming Contest (2018) Solution

Solution

A：Careful Thief

题意：给出n个区间，每个区间的每个位置的权值都是v，然后找长度为k的区间，使得这个区间的所有位置的权值加起来最大，输出最大权值， 所有区间不重叠

思路：贪心的想法，长度为k的区间的起始点肯定是某个区间的起始点，或者长度为k的区间的结束点肯定是某个区间的结束点。

因为存在最优的答案，它的起点不在某个区间的起点，那么只有两种情况。

1° 不属于任何已知区间

2° 在某个已知区间的内部

首先考虑第一种情况  如果不属于任何已知区间，那么根据贪心，我肯定能够往右移使得它是某个区间起点，这样得到的新的答案肯定大于等于原来的答案，因为我移动的这段区间的权值都为0

那么第二种情况，假如现在涵盖的区间横跨两个区间，那么我肯定能够右移结束点使得它与最后的那个区间的结束点对齐，或者左移起始点使得它跟最左边涵盖到的区间的起始点对齐，使得答案更大

然后双指针搞一搞

 #include <bits/stdc++.h>

 using namespace std;

 #define ll long long

 #define N 100010

 int t, m, k;

 struct node
 {
     int l, r;
     ll v;
     ll sum;
     inline node() {}
     inline node(int l, int r, int v) : l(l), r(r), v(v) {}

     inline void scan()
     {
         scanf("%d%d%lld", &l, &r, &v);
         sum = (ll)(r - l + ) * v;
     }

     inline bool operator < (const node& b) const
     {
         return l < b.l;
     }
 }arr[N]; 

 int main()
 {
     scanf("%d", &t);
     while (t--)
     {
         scanf("%d%d", &m, &k);
         for (int i = ; i <= m; ++i)
             arr[i].scan();

         sort(arr + , arr + m + );
         int L, R;
         int j = ;
         ll ans = ;
         ll tmp = ;
         for (int i = ; i <= m; ++i)
         {
             L = arr[i].l;
             R = L + k - ;
             while (arr[j].r <= R && j <= m)
             {
                 tmp += arr[j].sum;
                 ++j;
             }
             ll res = ;
             if(j <= m)
             {
                 res = arr[j].v * max(, R - arr[j].l + );
             }
             tmp += res;
             ans = max(ans, tmp);
             tmp -= res;
             tmp -= arr[i].sum;
         }
         tmp = ;
         j = m;
         for(int i = m; i >= ; --i)
         {
             R = arr[i].r;
             L = R - k + ;
             while(arr[j].l >= L && j >= )
             {
                 tmp += arr[j].sum;
                 --j;
             }
             ll res = ;
             if(j >= )
             {
                 res = arr[j].v * max(, arr[j].r - L + );
             }
             tmp += res;
             ans = max(ans, tmp);
             tmp -= res;
             tmp -= arr[i].sum;
         }
         printf("%lld\n",ans);
     }
     return ;
 }

B：Friends and Cookies

水。

 #include <bits/stdc++.h>

 using namespace std;

 #define ll long long

 #define N 1010

 int t, n;

 ll x;

 ll ans[N];

 int main()
 {
     scanf("%d", &t);
     while (t--)
     {
         scanf("%lld%d", &x, &n);
         if (n == )
         {
             printf("%lld\n", x);
             continue;
         }
         ll len = n + n - ;
         ll base = x / len;
         ll MOD = x % len;
         for (int i = ; i <= n; ++i)
         {
             if (i !=  && i != n)
                 ans[i] = base << ;
             else
                 ans[i] = base;
         }
         for (int i = ; i <= n && i <= MOD; ++i)
         {
             ans[i]++;
         }
         for (int i = n + ; i <= MOD; ++i)
         {
             ans[ * n - i]++;
         }
         for (int i = ; i <= n; ++i) printf("%lld%c", ans[i], " \n"[i == n]);
     }
     return ;
 }

C：Flip the Bits

水。

 #include <bits/stdc++.h>

 using namespace std;

 int t, n;

 int main()
 {
     scanf("%d", &t);
     while (t--)
     {
         scanf("%d", &n);
         if (n & )
         {
             puts("");
             continue;
         }
         else
         {
             int ans = ;
             while ((n & ) ==  && n)
             {
                 ++ans;
                 n >>= ;
             }
             printf("%d\n", ans);
         }
     }
     return ;
 }

D：Magic Sticks

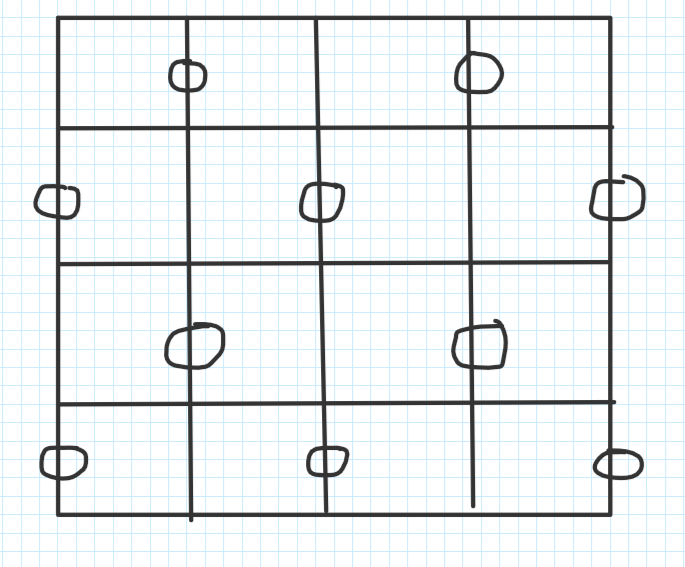
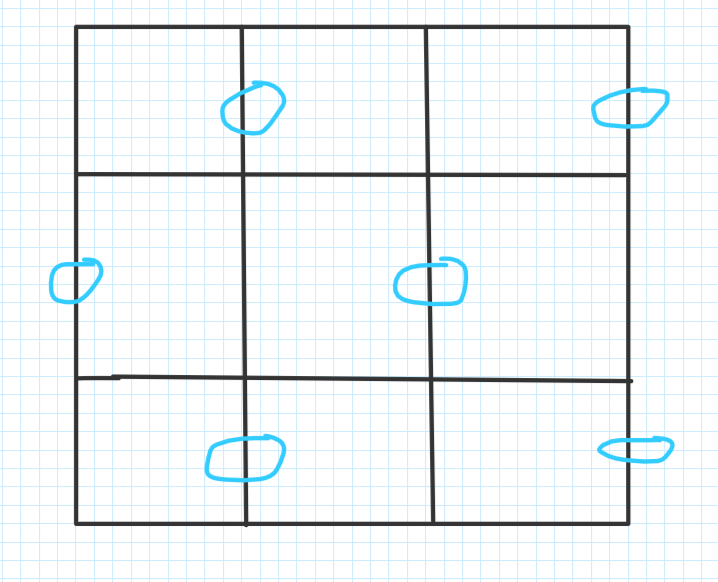
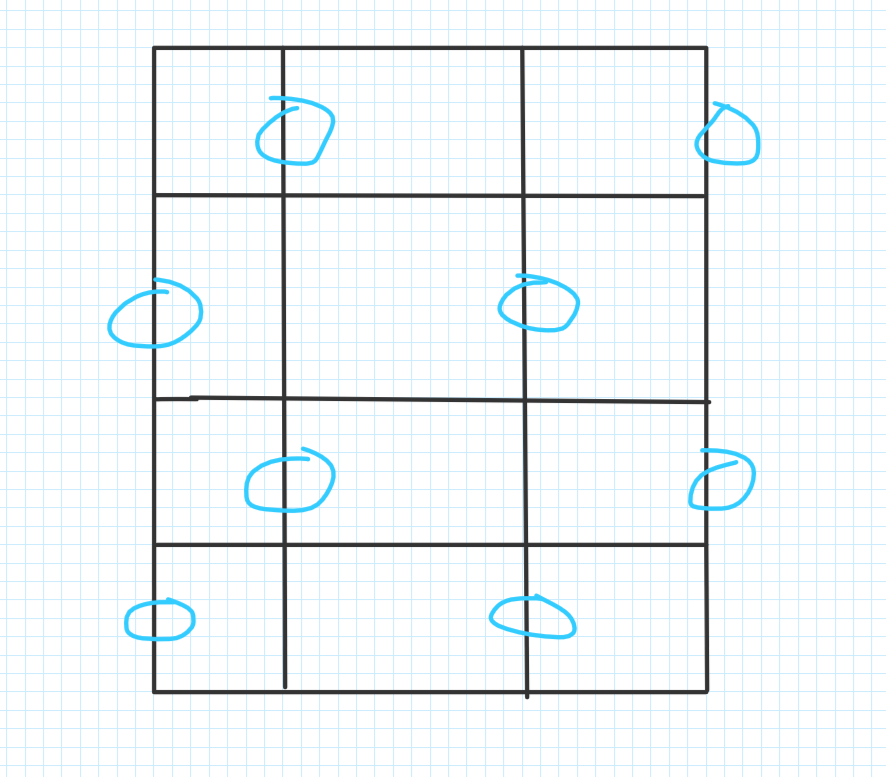
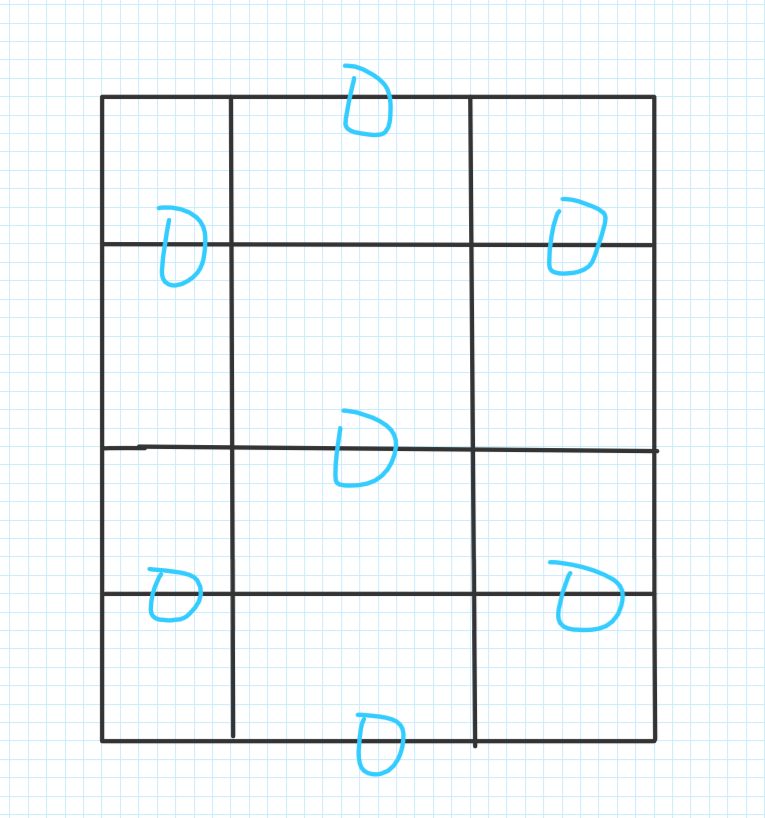
题意：有n * m 的矩形 每个矩形四条边，从这些边中选取一个边的集合，使得任意两条边不相交，并且每个矩形至少有一条边被选中

思路：

偶数 * 偶数

奇数 * 奇数

奇数 * 偶数

 #include <bits/stdc++.h>

 using namespace std;

 #define ll long long

 #define INFLL 0x3f3f3f3f3f3f3f3f

 int t;
 ll n, m;

 int main()
 {
     scanf("%d", &t);
     while (t--)
     {
         scanf("%lld%lld", &n, &m);

         ll ans = INFLL;

         if (n %  ==  && m %  == )
         {
             ans = min(ans, (n / ) * (m + ));
             ans = min(ans, (m / ) * (n + ));
         }
         else if (n %  ==  && m %  == )
         {
             ans = min(ans, ((n + ) / ) * m);
             ans = min(ans, ((m + ) / ) * n);
         }
         else
         {
             if (n %  == ) swap(n, m);
             ans = min(ans, ((n + ) /  * m));
             ans = min(ans, ((n + ) / ) * (m / ) + (n / ) * (m + ) / );
         }
         printf("%lld\n", ans);
     }
     return ;
 }

E：N - Dimensional Grid

题意： 在n维的空间，给你每个空间的长度，求有多少个格子相邻

思路：

一维：a1 - 1

二维：(a1 - 1) * a2 + (a2 - 1) * a1

大胆推广到高维：(a1 - 1) * _{(a2 + ... + an)  + (a2 - 1) * (a1 + a3 + ... + an) ...}

然后前缀后缀搞一搞

 #include<bits/stdc++.h>

 using namespace std;

 typedef long long ll;

 const int MOD = 1e9 + ;
 #define N 100010

 int t,n;
 ll arr[N],brr[N],crr[N];

 int main()
 {
     scanf("%d",&t);
     while(t--)
     {
         scanf("%d",&n);
         for(int i = ; i <= n; ++i)
         {
             scanf("%lld",&arr[i]);
         }
         brr[] = ;
         for(int i = ; i <= n; ++i)
         {
             brr[i] = (brr[i - ] * arr[i]) % MOD;
         }
         crr[n + ] = ;
         for(int i = n; i >= ; --i)
         {
             crr[i] = (crr[i + ] * arr[i]) %MOD;
         }
         ll ans = ;
         for(int i = ; i <= n; ++i)
         {
             ans = (ans + brr[i - ] * (arr[i] - ) %MOD * crr[i + ] %MOD) %MOD;
         }
         printf("%lld\n",ans);
     }
     return ;
 }

F：Minimum Sum of Array

题意：给出n个数，如果ai 可以整除aj，那么 ai 可以变成aj,求尽可能变换后，所有数的总和最小

思路：显然，贪心的想法是，对于每个数我们都给它变成这个数列中它跟它不互素的最小数，用类似素数筛法的思想去筛

 #include <bits/stdc++.h>

 using namespace std;

 #define N 100010

 #define M 1000010

 #define ll long long

 int t, n;
 int arr[N];
 int vis[M];
 int used[M];

 int main()
 {
     scanf("%d", &t);
     while (t--)
     {
         scanf("%d", &n);
         for (int i = ; i <= n; ++i)
             scanf("%d", arr + i);
         sort(arr + , arr +  + n);
         for (int i = ; i <= arr[n]; ++i)
             vis[i] = i, used[i] = ;
         for (int i = ; i <= n; ++i)
         {
             int v = arr[i];
             if (v >= (arr[n] /  + )) break;
             if (vis[v] == v && used[v] == )
             {
                 used[v] = ;
                 for (int j = v * ; j <= arr[n]; j += v)
                     vis[j] = min(vis[j], v);
             }
         }
         ll ans = ;
         for (int i = ; i <= n; ++i) ans += vis[arr[i]];
         printf("%lld\n", ans);
     }
     return ;
 }

G：Power of String

题意：给出一个式子，求修改最多k个字符，使得这个式子的值最大

思路：根据这个式子，我们可以知道假如一个字符有n个，那么这n个字符的值是(n * (n - 1)) / 2 * ASCII(ch)

那么我们可以把所有字符放在一起看

贪心的想法，如果存在答案，肯定是若干个小于等于k个字符变成同一个字符，因为这样会使得式子更大

那么我们枚举26个字符，使这个字符使要变成的字符

然后我们考虑，尽量让个数小的去换掉，那么个数小于等于k的字符就可以去做01背包，然后再枚举26位来当做补充

 #include <bits/stdc++.h> 

 using namespace std;

 #define READ freopen("Test.in", "r", stdin);
 #define N 100010
 #define M 5010
 #define ll long long
 #define INFLL 0x3f3f3f3f3f3f3f3f

 int t, n, K;
 char s[N];

 ll num[];

 inline ll F(ll x)
 {
     return (x * (x - )) / ;
 }

 inline ll Get(char c, ll pre, ll now)
 {
     ll res = ;
     res = F(now) * c;
     res -= F(pre) * c;
     return res;
 }

 ll dp[M];
 ll f[M];

 inline ll work(char c)
 {
     for (int i = ; i <= K; ++i) f[i] = -INFLL;
     for (int i = 'a'; i <= 'z'; ++i)
     {
         if (i == c) continue;
         if (num[i] == ) continue;
         dp[] = ;
         for (int j = ; j <= K; ++j) dp[j] = -INFLL;
         for (int j = 'a'; j <= 'z'; ++j)
         {
             if (j == c || j == i) continue;
             for (int l = K; l >= num[j]; --l)
                 dp[l] = max(dp[l], dp[l - num[j]] + Get(j, num[j], ));
         }
         ll tot = num[i];
         for (int j = K; j >= ; --j)
         {
             if (tot + j <= K)
                 dp[tot + j] = max(dp[tot + j], dp[j] + Get(i, tot, ));
             else
                 dp[K] = max(dp[K], dp[j] + Get(i, tot, tot - K + j));
         }
         for (int j = ; j <= K; ++j) f[j] = max(f[j], dp[j]);
     }
     ll res = ;
     for (int i = ; i <= K; ++i)
         res = max(res, f[i] + Get(c, num[c], num[c] + i));
     return res;
 } 

 int main()
 {
     #ifdef LOCAL
         READ;
     #endif
     scanf("%d", &t);
     while (t--)
     {
         scanf("%d%d", &n, &K);
         scanf("%s", s);
         memset(num, , sizeof num);
         for (int i = ; s[i]; ++i)
             num[s[i]]++;
         ll ans = , tmp = ;
         for (int i = 'a'; i <= 'z'; ++i)
             ans += F(num[i]) * i;
         tmp = ans;
         for (int i = 'a'; i <= 'z'; ++i)
             ans = max(ans, tmp + work(i));
         printf("%lld\n", ans);
     }
     return ;
 }

H：Making Friends

水。

 #include <bits/stdc++.h>

 using namespace std;

 #define N 2010

 int t, n;

 int arr[N];

 int main()
 {
     scanf("%d", &t);
     while (t--)
     {
         scanf("%d", &n);
         for (int i = ; i <= n * ; ++i)
             scanf("%d", arr + i);
         int ans = ;
         for (int i = ; i <= n; ++i)
             ans = max(ans, arr[i] + arr[ * n - i + ]);
         printf("%d\n", ans);
     }
     return ;
 }

I： Split the Number

水。

 #include <bits/stdc++.h>

 using namespace std;

 int t, x, n;

 int main()
 {
     scanf("%d", &t);
     while (t--)
     {
         scanf("%d%d", &x, &n);
         if (x < n)
         {
             puts("-1");
             continue;
         }
         int base = x / n;
         int MOD  = x % n;
         for (int i = ; i <= n; ++i)
         {
             printf("%d%c", base + ((n - i +  <= MOD) ?  : ), " \n"[i == n]);
         }
     }
     return ;
 }

J：T-Shirts Dilemma

题意：给出 a b v  在a - b 中找出一个连续子区间，使得这个区间内的所有数按位或运算的和小于v 找出子区间的最大长度

思路：

我们可以从最高有效位往最低有效为看 用 vi 表示 v 的第i位 ai bi 同理

如果vi == 0 && ai == 0 && bi == 0 那么我们跳到下一位继续看

如果vi == 1 && ai == 0 && bi == 0 那么答案就是 b - a + 1 因为 将a - b 的所有数按位或起来的值肯定小于 v' (v' = 将v的第i位边为0， 小于i的所有位都变为1) 并且 v' < v

如果 vi == 0 && ai == 0 && bi == 1

那么我们可以将bi 变为0 然后将小于i的b的所有位都变为1 再往下一位看 这样的操作相当于缩小了b的范围，对答案没有影响

如果vi == 1 && ai == 1 && bi == 1

显然 我们可以将 vi ai bi 都变为0 然后看下一位操作 是没有影响的

如果vi == 0 && ai == 1 && bi == 1 那么此时答案显然为0 因为a > v

如果vi ==1 && ai == 0 && bi == 1

如果此时 vi的低位都为1 那么答案就是 b - a + 1

如果不是 我们可以 令c = 将vi 变为0 然后所有低位都变为1 答案为 c - a + 1

或者 我们 可以将 a 变成 c + 1 然后 三个数的第i位都变为0 继续找下去

为什么将a 变成 c + 1 而不考虑 c + 1 一下的数

因为 c | c + 1 必然大于等于v 而 等于的情况 就是 b - a + 1 已经特判过

 #include <bits/stdc++.h>

 using namespace std;

 #define ll long long

 int t;

 ll a, b, v;

 inline ll work(ll a, ll b, ll v, int i)
 {
     if (i == -)
         return 1ll; 

     ll D = (1ll << i) - ;

     bool ai = a & (D + ), bi = b & (D + ), vi = v & (D + ); 

     if (vi && !ai && !bi)
         return b - a + ;
     if (!vi && ai && bi)
         return ;
     if (vi && ai && bi)
         return work(a & D, b & D, v & D, i - );
     if (!vi && !ai && !bi)
         return work(a, b, v, i - );
     if (!vi && !ai && bi)
         return work(a, (1ll << i) - , v, i - ); 

     if (v == ((1ll << (i + )) - ))
         return b - a + ;

     ll c = (1ll << i) - ;
     return max(c - a + , work(, b & D, v & D, i - ));
 }

 int main()
 {
     #ifdef LOCAL
         freopen("Test.in", "r", stdin);
     #endif
     scanf("%d", &t);
     while (t--)
     {
         scanf("%lld%lld%lld", &a, &b, &v);
         printf("%lld\n", work(a, b, v, ));
     }
     return ;
 }

K：League of Demacia

题意：给定一个原点，给定一条边长为z的线段，使得原点为中点，角度不定。从该线段两端点向同一方向画出两条射线，使得这一区域的点超过m个。

思路：显然我们可以枚举每一个点在射线上的情况，然后o（n）枚举每个点的情况。确定某一点是否在区域内可通过向量的数量积与z/2的比较以及向量积来确定是否为同一方向。

 #include<bits/stdc++.h>

 using namespace std;

 #define N 1010

 const double eps = 1e-;

 inline int sgn(double x)
 {
     if(fabs(x) < eps) return ;
     else if(x > ) return ;
     else return -;
 }

 struct Point{
     double x, y;
     inline Point(){}
     inline Point(double x, double y) : x(x), y(y){}

     inline void input()
     {
         scanf("%lf %lf",&x, &y);
     }

     inline Point operator - (const Point &b) const
     {
         return Point(x - b.x, y - b.y);
     }

     inline double operator ^ (const Point &b) const
     {
         return x * b.y - y * b.x;
     }    

     inline double operator * (const Point &b) const
     {
         return x * b.x + y * b.y;
     }

     inline Point operator + (const Point &b) const
     {
         return Point(x + b.x, y + b.y);
     }

     inline Point operator / (const double &k) const
     {
         return Point(x / k, y / k);
     }

     inline double distance(const Point &b) const
     {
         return hypot(x - b.x, y - b.y);
     }

     inline Point rotate(Point p, double angle)
     {
         Point v = (*this) - p;
         double c = cos(angle), s = sin(angle);
         return Point(p.x + v.x * c - v.y * s, p.y + v.x * s + v.y * c);
     }
 }P[N];

 int n, m;
 double z;

 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--)
     {
         scanf("%d %d %lf",&n, &m, &z);
         double r = z / ;
         for(int i = ; i <= n; ++i)
         {
             P[i].input();
         }
         bool flag = false;
         for(int i = ; i <= n; ++i)
         {
             Point a = P[i];
             double d = a.distance(Point(, ));
             if(sgn(d) == ) a = Point(, );
             else if(sgn(d - r) <= ) a = P[i];
             else a = P[i].rotate(Point(, ), acos(r / d));

             a = a / a.distance(Point(, ));
             int cnt = ;
             for(int j = ; j <= n; ++j)
             {
                 if(i == j) continue;
                 double tmp = fabs(P[j] * a);
                 if(sgn(tmp - r) <=  && sgn(a ^ P[j]) <= ) cnt++;
                 if(cnt >= m) break;
             }
             if(cnt >= m)
             {
                 flag = true;
                 break;
             }
         }
         puts(flag ? "Yes" : "No");

     }
     return ;
 }

L：Lazy Teacher

题意：对一个nm的矩阵填色，一共有k个颜色，相邻的方块不能同一种颜色，求填色方案。

思路：首先注意到n很小，其次当我们按顺序填方格时，影响这一方格以及接下来的方格的只会是前5块，因此我们只用记录前5块方格即可。因此对于每一个长度为6的方块实际上最多用到6种颜色，我们将其离散化后，那么最远的方块p1<1，p2<2,p3<3,p4<4,p5<5

然后我们可以枚举当前要填充颜色的方块的颜色，从0-5，其中5代表和前面5块互不相同个颜色，然后搜索一下（或者说dp？），最后剪剪枝。

 #include<bits/stdc++.h>

 using namespace std;

 typedef long long ll;

 const int MOD = 1e9 + ;

 #define M 10010

 int val[], pos[];
 ll dp[][M][][][][];

 int limit;
 int n, m, k;

 inline void update()
 {
     memset(val, , sizeof val);
     for (int i = , color = ; i < ; ++i)
     {
         if (val[pos[i]] != )
         {
             pos[i] = val[pos[i]] - ;
         }
         else
         {
             val[pos[i]] = color;
             pos[i] = color - ;
             color++;
         }
     }
 }

 inline ll solve(int x, int y, int p2, int p3, int p4, int p5)
 {
     if (x == n) return solve(, y + , p2, p3, p4, p5);
     if (y == m) return ;
     if (dp[x][y][p2][p3][p4][p5] != -) return dp[x][y][p2][p3][p4][p5];
     int res = ;
     int up;
     if (n == )
     {
         up = ;
     }
     else if (n == )
     {
         up = p2;
     }
     else if (n == )
     {
         up = p3;
     }
     else if (n == )
     {
         up = p4;
     }
     else if (up = )
     {
         up = p5;
     }
     for (int color = ; color < limit; ++color)
     {
         if (color == up && y != ) continue;//up
         if (color == p5 && x != ) continue;//left
         pos[] = p2, pos[] = p3, pos[] = p4, pos[] = p5, pos[] = color;
         update();//离散化
         res = (res + (color ==  ? k -  : ) * solve(x + , y, pos[], pos[], pos[], pos[])) % MOD;//5 means new color
     }
     dp[x][y][p2][p3][p4][p5] = res;
     return res;
 }

 int main()
 {
     int t;
     scanf("%d", &t);
     while (t--)
     {
         scanf("%d %d %d", &n, &m, &k);
         limit = min(k, );
         memset(dp, -, sizeof dp);
         ll ans = solve(, , , , , );
         printf("%lld\n", ans);
     }
     return ;
 }

M：Greedy Pirate

题意：给出一棵树，n - 1条边，一条边上两个权值，然后每次询问u -> v  问 从 u - > v的最大花费，每条边可以走两次

思路：显然 答案是所有边权和减去 终点到LCA的权值和 减去 LCA 到 起点的权值和

 #include<bits/stdc++.h>

 using namespace std;

 const int maxn = ;
 const int DEG = ;

 typedef long long ll;
 int n;

 struct Edge{
     int to,nxt;
     int w1,w2;
     inline Edge(){}
     inline Edge(int to,int nxt,int w1,int w2):to(to),nxt(nxt),w1(w1),w2(w2){}
 }edge[maxn << ];

 int head[maxn],tot;

 inline void addedge(int u,int v, int w1, int w2)
 {
     edge[tot] = Edge(v,head[u],w1,w2);
     head[u] = tot++;
 }

 int fa[maxn][DEG];
 ll dis1[maxn];// from fa
 ll dis2[maxn];// to fa
 int deg[maxn];

 void init()
 {
     tot = ;
     memset(dis1, , sizeof dis1);
     memset(dis2, , sizeof dis2);
     memset(head, -, sizeof head);
 }

 inline void BFS(int root)
 {
     queue<int>q;
     deg[root] = ;
     fa[root][] = root;
     q.push(root);
     while(!q.empty())
     {
         int tmp = q.front();
         q.pop();
         for(int i = ; i < DEG; ++i)
         {
             fa[tmp][i] = fa[fa[tmp][i - ]][i - ];
         }
         for(int i = head[tmp]; ~i; i = edge[i].nxt)
         {
             int v = edge[i].to;
             if(v == fa[tmp][]) continue;
             dis1[v] = dis1[tmp] + edge[i].w1;
             dis2[v] = dis2[tmp] + edge[i].w2;
             deg[v] = deg[tmp] + ;
             fa[v][] = tmp;
             q.push(v);
         }
     }
 }

 int LCA(int u,int v)
 {
     if(deg[u] > deg[v]) swap(u, v);
     int hu = deg[u], hv = deg[v];
     int tu = u;
     int tv = v;
     for(int det = hv - hu, i = ; det; det >>= , ++i)
     {
         if(det & )
             tv = fa[tv][i];
     }
     if(tu == tv) return tu;
     for(int i = DEG - ; i >= ; --i)
     {
         if(fa[tu][i] == fa[tv][i]) continue;
        tu = fa[tu][i];
        tv = fa[tv][i];
     }
     return fa[tu][];
 }

 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--)
     {
         init();
         scanf("%d",&n);
         ll sum = ;
         for(int i = ; i < n; ++i)
         {
             int u, v, w1, w2;
             scanf("%d %d %d %d",&u, &v, &w1, &w2);
             sum += w1 + w2;
             addedge(u, v, w1, w2);
             addedge(v, u, w2, w1);
         }
         BFS();
         int q;
         scanf("%d",&q);
         while(q--)
         {
             int u,v;
             scanf("%d %d",&u,&v);
             int root = LCA(u,v);
             ll ans = sum - (dis2[v] - dis2[root] + dis1[u] - dis1[root]);
                printf("%lld\n",ans);
         }
     }
     return ;
 }