最短路径算法（I）

弗洛伊德算法(Floyed-Warshall)

适用范围及时间复杂度

该算法的时间复杂度为O（N^3），适用于出现负边权的情况。

可以求取最短路径或判断路径是否连通。可用于求最小环，比较两点之间的大小。

（什么？？你不知道什么是负边权？？戳->http://t.cn/Ef7pbu6）

核心思想

对于任意一个K点，i到j的距离有两种可能：要么经过k点，要么不经过k点。所以我们只需要不断的迭代k，比较d[i][k]与d[i][k]+d[k][j]的值。如果后者更短，则更新d[i][k]的值。如此重复，最后检查完所有的k时，我们便得到了最短距离。

注意事项及常见问题

由核心思想不难看出，这个算法需要三层循环来实现。但k的位置是值得注意的。经过分析不难发现，k属于最外层循环。

i,j,k三点并不能相同。如若相同，则算法无意义。（自己到自己的距离当然是零啦）

在使用算法时，将map[i][j]值初始为最大/小，map[i][i]一定设置为0（自己到自己当然是零啦）

有时题目会暗含重复数据，也就是相同的路径权重不同。所以要根据题目进行数据比较，更新最大/小的值。

代码实现

初始化：如若两点（假定两点为u,v）相连，则其最短路径初始化为权重。如不相连则初始化为巨大值（0x7ffffff）

 if(w[u][v]){
     dis[u][v]=w[u][v];
 }else{
     dis[u][v]=*7ffffff;
 }

戳开查看

step2:寻找中间点K，比较距离并判断是否更新。

 for(int k=;k<=n;k++){
     for(int i=;i<=n;i++){
         for(int j=;j<=n;j++){
             if(i!=k&&i!=j&&j!=k){
                 dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
             }
         }
     }
 }

戳开查看

迪杰斯特拉算法(dijkstra)

适用范围及时间复杂度

单源路径算法，只计算起点只有一个的情况。不可以用于处理存在负边权的情况。时间复杂度O（N^2）

多用于计算一个结点到其他所有结点的最短路径。以起始点为中心向外层扩展,直到扩展到终点为止。

核心思想

对于图中一个点G（V,E），可以被归为以下两组集合之一：

■白点集合:指已确定最短路径的顶点集合。用S表示,初始时S中只有一个元素,即源点,以后每求得一条最短路径,就加入到集合S中,直到全部顶点都加入S中,算法就结束了。

■蓝点集合:指未确定最短路径的顶点集合。用U表示,按最短路径长度的递增次序把第二组的顶点加入到S中。在加入过程中,总是寻找到与起点距离最短的先加入,保持集合S中的路径长度永远比集合U中的小。
用vis[v]标记顶点v是白点还是蓝点,白点用vis[v]=true标记,蓝点用vis[v]=false标记。很显然,初始化时,所有vis除源点为true外,其它均为false;

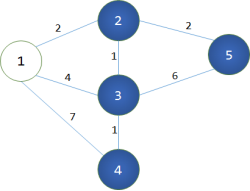第1轮循环找到dis[1]最小,将1变成白点。对所有与之相连的蓝点做出改,使得:dis[2]=2;dis[3]=4;dis[4]=7;此时dis[2],dis[3],dis[4]被它最后一个中转点修改了最短路径。

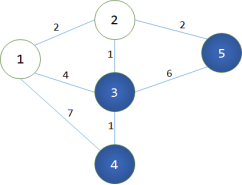第2轮循环找到dis[2]最小,将2变成白点。对所有与之相连的蓝点做出修改,使得:dis[3]=3;dis[5]=4;此时,dis[3],dis[5]被它最后一个中转点修改了最短路径

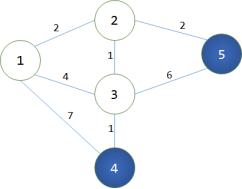第3轮循环找到dis[3]最小,将3变为白点。对所有与之相连的蓝点做出修改,使得:dis[4]=4,而dis[5]之前已经计算出来等于4了,现在不能用9去修改。说明点3不是5的最后一个中转点。此时dis[4]被它最后一个中转点修改了最短路径。
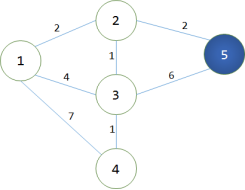第4轮循环找到dis[4]最小,将4变成白点。但点4没有与之相连的蓝点,故不需要做出修改。
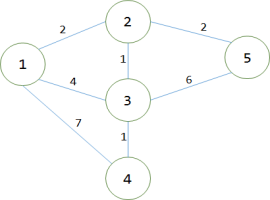第5轮循环找到dis[5]最小,把5置为白点,而已经没有与5相连接的蓝点。故无须更改。
如此过后，便得到了起点至各点的单源最短路径。

代码实现

我们至少需要三个数组来存储数据（邻接矩阵法）。暂定map[][]为邻接矩阵，s为起点，e为终点，dis[i]表示i点到源点的最短路径。bool vis[]表示该点为蓝点或白点。

初始化

 for(int i=;i<=n;i++)
     for(int j=;j<=n;j++) g[i][j]=maxx;
     for(int i=;i<=n;i++) dis[i]=map[s][i]; //为dis赋初值
     vis[s]=true; //起点标记为已访问
     dis[s]=; //起点标记为白点

算法核心

     for(int i=;i<=n-;i++){
         minx=maxx;
         for(int j=;j<=n;j++)
             if(!vis[j]&&dis[j]<minx){
                 minx=dis[j]; //不断寻找dis的最小值,并把坐标保存在u中
                 u=j;
             }
         if(u==) break; //没找到蓝点,退出循环
         vis[u]=true; //把找到的蓝点值为已访问
         for(int v=;v<=n;v++)
             //如果j到起点的最短路径大于k到起点的最短路径+k到j的距离,则更新dis[j]
             dis[v]=min(dis[v],dis[v]+map[u][v]);
     }
     printf("%.2lf\n",dis[t]);

注意事项

dijskstra算法有两重循环,第一重循环是1到n-1,第二重循环是1到n。这中间可以优化的是,如果在接收数据的时候,保存最大的点p,这样,第一重循环就只需要扫描到p-1,而第二重循环只需要扫描到p。降低了时间复杂度。但多数时候,题目是给定了最大的点,不需要再找了。

 for(int i=;i<=n;i++){
     scanf("%d%d%d",&u,&v,&w);
     if(g[u][v]>w) g[u][v]=g[v][u]=w;
     p=max(p,max(u,v));
 }

队列优化

priority_queue< pair<int,int> > q;
void Dijkstra()
{
    memset(Distrance,0x3f,sizeof(Distrance));
    Distrance[]=;
    q.push(make_pair(,));
    while(q.size())
    {
        int x=q.top().second;
        q.pop();
        if(Vist[x])
            continue;
        Vist[x]=true;
        for(int i=Head[x]; i; i=Edges[i].Next)
        {
            int y=Edges[i].End;int z=Edges[i].Val;
            if(Distrance[y]>Distrance[x]+z)
            {
                Distrance[y]=Distrance[x]+z;
                q.push(make_pair(-Distrance[y],y));
            }
        }
    }
}