POJ2479,2593: 两段maximum-subarray问题

虽然是两个水题，但是一次AC的感觉真心不错

这个问题算是maximum-subarray问题的升级版，不过主要算法思想不变：

1. maximum-subarray问题

maximum-subarray就是找到数组A[1....n]中的连续子数组A[i.....j]并且A[i]+...+A[j]和最大。当然了，(1<=i<=j<=n)。

maximum-subarray的O(n)解法就是从左到右扫描数组A，另外设置一工具数组DP,DP数组的作用就是记录以当前下标为终止下标的子数组和。比如DP[j]=A[i]+....+A[j](A[i] 到 A[j]是连续的）。现在假设我们已经求出DP[j]，数组即将扫描A[j+1]，则DP[j]与DP[j+1]的关系描述如下：

DP[j+1]=(DP[j]>0)? (DP[j]+A[j+1]) : (A[j+1]).

因为DP[j+1]要求出以j+1下标为结束下标的子数组和，而且DP[j]已经求出，所以我们要判断DP[j]是否为正数，如为正，则加上A[j+1]。如为负，那么很明显的，A[i]+.....+A[j]+A[j+1]<A[j+1], 所以要让DP[j+1]=A[j+1]。

2. 求两个maximum-subarray问题

这两个maximum-subarray不相交。

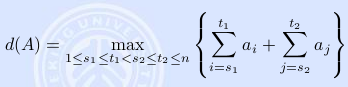
我们可以设置一个“分水岭”，假设为k，那么maximum-subarray(A[1..k]) + maximum-subarray(A[k+1..n])就是我们要的解。

当然如果我们枚举每一个k值（1<=k<=n-1)的话，因为题目开出的N值为50000，真个时间复杂度为O(n^2)，必然超时。

所以我们可以再设两个工具数组：lmax和rmax，lmax[i]表示A[1]到A[i]的最大子数组和，rmax[i]=A[i+1]....A[n]的最大子数组和。再次明确一下：lmax/rmax数组与DP数组的不同。

假设DP[s]=A[p+..q+..+r+..s], 那么lmax[s]可能就等于A[q+...+r]或者A[p+...+r]或者等等。

然后我们得到每个lmax[k]+rmax[k]，对k进行枚举，lmax[k]+rmax[k]值最大的即为最后的解。

附上POJ2593代码：（POJ2479改动一点就可以了）

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<map>
#include<vector>
using namespace std;
const int max_size=;
int n,a[max_size];
int ldp[max_size],rdp[max_size],ans,inf=<<;
int lmax[max_size],rmax[max_size];
int main(){
    while(scanf("%d",&n)!=EOF&&n){
        memset(a,,sizeof(a));
        memset(ldp,,sizeof(ldp));
        memset(rdp,,sizeof(rdp));
        memset(lmax,,sizeof(lmax));
        memset(rmax,,sizeof(rmax));
        ans=-inf;
        for(int i=;i<=n;i++){
            scanf("%d",&a[i]);
        }
        lmax[]=ldp[]=a[];
        for(int i=;i<=n;i++){
            if(ldp[i-]>) ldp[i]=ldp[i-]+a[i];
            else ldp[i]=a[i];
            ans=max(ans,ldp[i]);
            lmax[i]=ans;
        }
        rmax[n]=rdp[n]=a[n];
        ans=-inf;
        for(int i=n-;i>=;i--){
            if(rdp[i+]>) rdp[i]=rdp[i+]+a[i];
            else rdp[i]=a[i];
            ans=max(ans,rdp[i]);
            rmax[i]=ans;
        }
        ans=-inf;
        for(int k=;k<=n-;k++){
            ans=max(ans,lmax[k]+rmax[k+]);
        }
        printf("%d\n",ans);
    }
}