[原博客] POJ 1704 Georgia and Bob

题目链接
题意：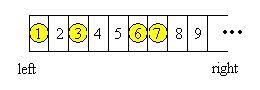

如图，Georgia和Bob在玩游戏。一个无限长的棋盘上有N个旗子，第i个棋子的位置可以用Pi表示。现在Georgia先走。每个人每一次可以把一枚棋子向左移动任意个格子，但是不能超越其他棋子，也不能和其他棋子处在同一个格子里。如果轮到某一个人的时候Ta再也不能移动棋子了，就判负。现在每个测试数据给定一种情况，如果Georgia会赢，输出“Georgia will win”，如果Bob会赢，输出“Bob will win”，如果不确定，输出“Not sure”。两个人都知道获胜策略是什么，也会想方设法取得胜利。

首先说明，这种没有平局的博弈是不可能"Not sure"的，每个状态不是必胜就是必败，参见定义。
我们发现每次只能把一个旗子往左移动，所以是和这些旗子之间的距离有密切关系的，把图片上的距离表示出来就是：0，1，2，0，记为数列。
然后注意每次移动一个旗子，实际上是把数列中的一个数减小x，数列中的下一个数增加x。（若移动第N个，只减少不增加）
我们把数列中的这些数分为两类，一种是A类：由数列的第N项，N-2，N-4,N-6……项组成；另一种是B类：由数列的第N-1项，N-3，N-5，N-7……项组成。
这样每次操作实际上就是把A类数的一项减少，B类数的一项增加。（或者仅仅A类的第N项减少）
我们可以证明B类上的数是不影响胜负的。
对称博弈，设有一个人移动的是B类中数列的第i项，那么另一个人下一盘就可以把上次他移动的旗子移动到第i+2项，注意还是B类，知道移到第N项移出为止。

所以如果我们只看A类的数，就是一个Nim取石子游戏，Xor起来就好了。

ps.读入后需要排序（样例都有序），大坑。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>

//by zrt
//problem:
using namespace std;
typedef long long LL;
const int inf(0x3f3f3f3f);
);
int tt;
];
];
int main(){
    #ifdef LOCAL
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif
    scanf("%d",&tt);
    while(tt--){
        int n;
        scanf("%d",&n);
        ;i<=n;i++) scanf("%d",&a[i]);
        sort(a,a+n+);
        ;i<=n;i++) b[i]=a[i]-a[i-]-;
        ;
        ;i-=){
            sg^=b[i];
        }
        if(!sg) puts("Bob will win");
        else puts("Georgia will win");
    }

    ;
}