【转载】 强化学习（三）用动态规划（DP）求解

原文地址：

https://www.cnblogs.com/pinard/p/9463815.html

-----------------------------------------------------------------------------------------------

在强化学习（二）马尔科夫决策过程(MDP)中，我们讨论了用马尔科夫假设来简化强化学习模型的复杂度，这一篇我们在马尔科夫假设和贝尔曼方程的基础上讨论使用动态规划(Dynamic Programming, DP)来求解强化学习的问题。

　　　　动态规划这一篇对应Sutton书的第四章和UCL强化学习课程的第三讲。

1. 动态规划和强化学习问题的联系

对于动态规划，相信大家都很熟悉，很多使用算法的地方都会用到。就算是机器学习相关的算法，使用动态规划的也很多，比如之前讲到的隐马尔科夫模型HMM（二）前向后向算法评估观察序列概率，隐马尔科夫模型HMM（四）维特比算法解码隐藏状态序列， 都是动态规划的典型例子。

动态规划的关键点有两个：一是问题的最优解可以由若干小问题的最优解构成，即通过寻找子问题的最优解来得到问题的最优解。第二是可以找到子问题状态之间的递推关系，通过较小的子问题状态递推出较大的子问题的状态。而强化学习的问题恰好是满足这两个条件的。

　　　　我们先看看强化学习的两个基本问题。

　　　　那么如何找到动态规划和强化学习这两个问题的关系呢？

　　　　回忆一下上一篇强化学习（二）马尔科夫决策过程(MDP)中状态价值函数的贝尔曼方程：

从这个式子我们可以看出，我们可以定义出子问题求解每个状态的状态价值函数，同时这个式子又是一个递推的式子, 意味着利用它，我们可以使用上一个迭代周期内的状态价值来计算更新当前迭代周期某状态ssSSS的状态价值。可见，使用动态规划来求解强化学习问题是比较自然的。

2. 策略评估求解预测问题

　　　　首先，我们来看如何使用动态规划来求解强化学习的预测问题，即求解给定策略的状态价值函数的问题。这个问题的求解过程我们通常叫做策略评估(Policy Evaluation)。

　　　　策略评估的基本思路是从任意一个状态价值函数开始，依据给定的策略，结合贝尔曼期望方程、状态转移概率和奖励同步迭代更新状态价值函数，直至其收敛，得到该策略下最终的状态价值函数。

　　　　下面我们用一个具体的例子来说明策略评估的过程。

3. 策略评估求解实例

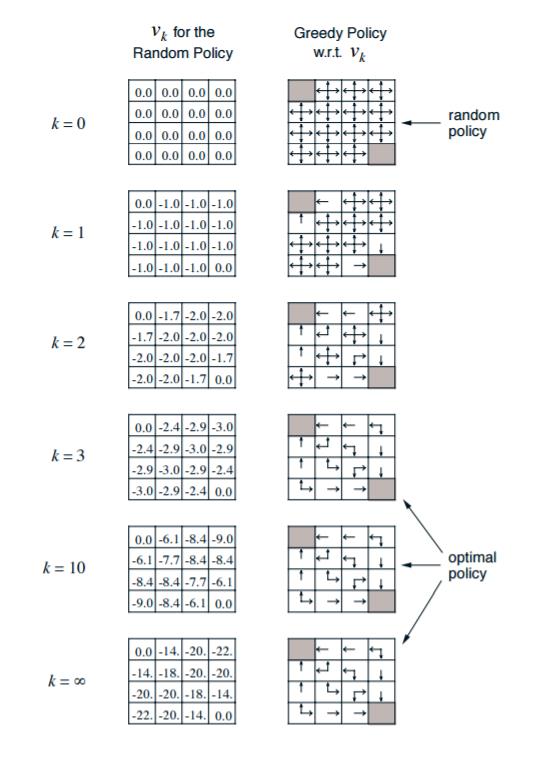
可以看到，动态规划的策略评估计算过程并不复杂，但是如果我们的问题是一个非常复杂的模型的话，这个计算量还是非常大的。

4. 策略迭代求解控制问题

　　　　上面我们将了使用策略评估求解控制问题，现在我们再来看如何使用动态规划求解强化学习的第二个问题控制问题。一种可行的方法就是根据我们之前基于任意一个给定策略评估得到的状态价值来及时调整我们的动作策略，这个方法我们叫做策略迭代(Policy Iteration)。

　　　　如何调整呢？最简单的方法就是贪婪法。考虑一种如下的贪婪策略：个体在某个状态下选择的行为是其能够到达后续所有可能的状态中状态价值最大的那个状态。还是以第三节的例子为例，如上面的图右边。当我们计算出最终的状态价值后，我们发现，第二行第一个格子周围的价值分别是0,-18,-20，此时我们用贪婪法，则我们调整行动策略为向状态价值为0的方向移动，而不是随机移动。也就是图中箭头向上。而此时第二行第二个格子周围的价值分别是-14,-14,-20, -20。那么我们整行动策略为向状态价值为-14的方向移动，也就是图中的向左向上。

　　　　如果用一副图来表示策略迭代的过程的话，如下图：

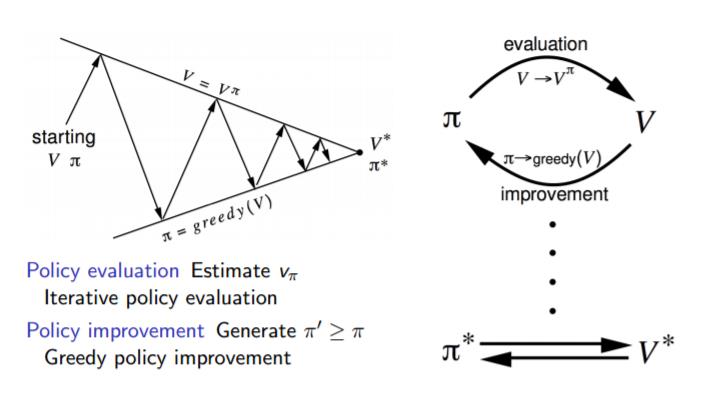
5. 价值迭代求解控制问题

和上一节相比，我们没有等到状态价值收敛才调整策略，而是随着状态价值的迭代及时调整策略, 这样可以大大减少迭代次数。此时我们的状态价值的更新方法也和策略迭代不同。现在的贝尔曼方程迭代式子如下：

　　　　可见由于策略调整，我们现在价值每次更新倾向于贪婪法选择的最优策略对应的后续状态价值，这样收敛更快。

6. 异步动态规划算法

　　　　在前几节我们讲的都是同步动态规划算法，即每轮迭代我会计算出所有的状态价值并保存起来，在下一轮中，我们使用这些保存起来的状态价值来计算新一轮的状态价值。

　　　　另一种动态规划求解是异步动态规划算法，在这些算法里，每一次迭代并不对所有状态的价值进行更新，而是依据一定的原则有选择性的更新部分状态的价值，这类算法有自己的一些独特优势，当然有额会有一些额外的代价。

　　　　常见的异步动态规划算法有三种：

　　　　第一种是原位动态规划 (in-place dynamic programming)， 此时我们不会另外保存一份上一轮计算出的状态价值。而是即时计算即时更新。这样可以减少保存的状态价值的数量，节约内存。代价是收敛速度可能稍慢。

　　　　第二种是优先级动态规划 (prioritised sweeping)：该算法对每一个状态进行优先级分级，优先级越高的状态其状态价值优先得到更新。通常使用贝尔曼误差来评估状态的优先级，贝尔曼误差即新状态价值与前次计算得到的状态价值差的绝对值。这样可以加快收敛速度，代价是需要维护一个优先级队列。

　　　　第三种是实时动态规划 (real-time dynamic programming)：实时动态规划直接使用个体与环境交互产生的实际经历来更新状态价值，对于那些个体实际经历过的状态进行价值更新。这样个体经常访问过的状态将得到较高频次的价值更新，而与个体关系不密切、个体较少访问到的状态其价值得到更新的机会就较少。收敛速度可能稍慢。

7. 动态规划求解强化学习问题小结

　　　　动态规划是我们讲到的第一个系统求解强化学习预测和控制问题的方法。它的算法思路比较简单，主要就是利用贝尔曼方程来迭代更新状态价值，用贪婪法之类的方法迭代更新最优策略。

　　　　动态规划算法使用全宽度（full-width）的回溯机制来进行状态价值的更新，也就是说，无论是同步还是异步动态规划，在每一次回溯更新某一个状态的价值时，都要回溯到该状态的所有可能的后续状态，并利用贝尔曼方程更新该状态的价值。这种全宽度的价值更新方式对于状态数较少的强化学习问题还是比较有效的，但是当问题规模很大的时候，动态规划算法将会因贝尔曼维度灾难而无法使用。因此我们还需要寻找其他的针对复杂问题的强化学习问题求解方法。

　　　　下一篇我们讨论用蒙特卡罗方法来求解强化学习预测和控制问题的方法。

（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com） 　　　　

-------------------------------------------------------------------------------------------------------------