查找->动态查找表->B+树(无代码)

文字描述

B+树定义

　　B+树是应文件系统所需而出的一种B-树的变型树。一棵m阶的B+树和m阶的B-树的差异在于：

　　(1)有n棵子树的结点中含有n个关键字

　　(2)所有的叶子结点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子结点本身依关键字的大小从小到大顺序链接。

　　(3)所有的非终端结点可以看成是索引部分，结点中仅含有其子树中的最大(或最小)关键字。

B+树查找算法

　　通常B+树上有两个头指针，一个指向根结点，另一个指向关键字最小的叶子结点。因此，可以对B+树进行两种查找运算：一种是从最小关键字起顺序查找，另一种是从根结点开始进行随机查找。

　　在B+树上进行随机查找时，若非终端结点上的关键字等于给定值，并不终止，而是继续向下直到叶子结点。因此，在B+树上进行随机查找，不管查找成功与否，每次查找都是走了一条从根到叶子结点的路径。

B+树插入算法

　　B+树的插入仅在叶子结点上进行，当结点中的关键字个数大于m时要分裂成两个结点，它们所含关键字个数分别为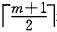和

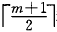
。并且，它们的双亲结点中应同时包含这两个结点中的最大关键字。

B+树删除算法

　　B+树的删除也仅在叶子结点进行，当叶子结点中的最大关键字被删除时，其在非终端结点中的值可以作为一个“分界关键字”。若因删除而使结点关键字的个数少于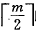时，其和兄弟结点的合并过程亦和B-树类似。

示意图

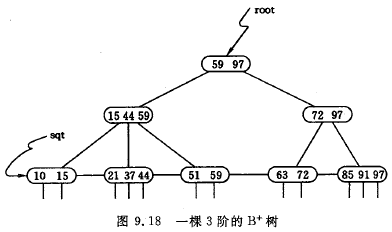
算法分析

B+树的查找分析类似于B-树。

代码实现

略