C语言---斐波那契问题

  最近学习了一个叫递归的概念，里面最著名的一个例子就是斐波那契问题，觉得很有意思，就来实现一下：

什么是斐波那契数列

  斐波那契数列，又称黄金分割数列，值得这样一个数列：0、1、1、3、5、8、13、21、34、……在数学上，斐波那契数列以如下形式递归方法定义：



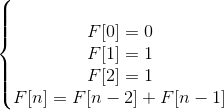
&emsp；&emsp；这是一个线性递推数列。

递归实现方式：

Demo：

#include <stdio.h>
//recursive fibonacci
int rec_fibo(int n)
{
    if(n == 1 || n == 2)
        return 1;
    if(n > 2)
        return (rec_fibo(n - 2) + rec_fibo(n - 1));
}
int main(void)
{
    int n = 0;
    //提醒user输入
    printf("please input you want to test number:\n");
    scanf("%d", &n);
    int fi_num = 0;
    //调用rec_fibo()函数
    fi_num = rec_fibo(n);
    //向屏幕输出
    printf("F[%d] = %d\n", n, fi_num);
    return 0;
}

---

非递归实现方式：

Demo：

//fibonacci non-recursive implementation
int non_rec_fibo(int n)
{
    //定义一个临时储存数组来存储
    int temp[2];
    //分别给0,1下标的数组赋初值
    temp[0] = 1;
    temp[1] = 1;

    int i = 0;
    if(n == 1 || n == 2)
        return 1;
    else
    {
        for(i = 2; i < n; i++)
        {
            //进行数组内部的数据转换
            int tp = temp[0] + temp[1];
            temp[1] = temp[0];
            temp[0] = tp;
        }
        return temp[0];
    }
}
int main(void)
{
    int n = 0;
    printf("please input you want to test number:\n");
    scanf("%d", &n);
    int fi_num = 0;
    fi_num = non_rec_fibo(n);
    printf("F[%d] = %d\n", n, fi_num);
    return 0;
}

  ok这里已经完整的说明了斐波那契数列的两种思想！！！

null