【2016北京集训测试赛（二）】 thr （树形DP）

Description

题解

　　（这可是一道很早就碰到的练习题然后我不会做不想做，没想到在Contest碰到欲哭无泪......）

　　题目大意是寻找三点对的个数，使得其中的三个点两两距离都为d。

　　问题在于，这个d不是定值啊，这使得DP的进行比较困难。

　　于是这个神奇解法在DP过程中把d省去了！

状态表示　　

　　$f [u][i]$： 以u为根的子树内，到u的距离为i的节点个数，$f [u][0]=1$ 。

　　$g [u][i]$：以u为根的子树内，存在多少点对 (a,b)，它们到它们的lca的距离都为d，且它们的lca到u的距离恰好为d-i。

　　Wait?What? 为什么出现了d？为什么是d-i？d不是一个不确定的值吗？g是个什么鬼？

　　（额看图看图，f应该很容易懂吧，我们现在来弄懂g）

　　g的示意图：

　  　

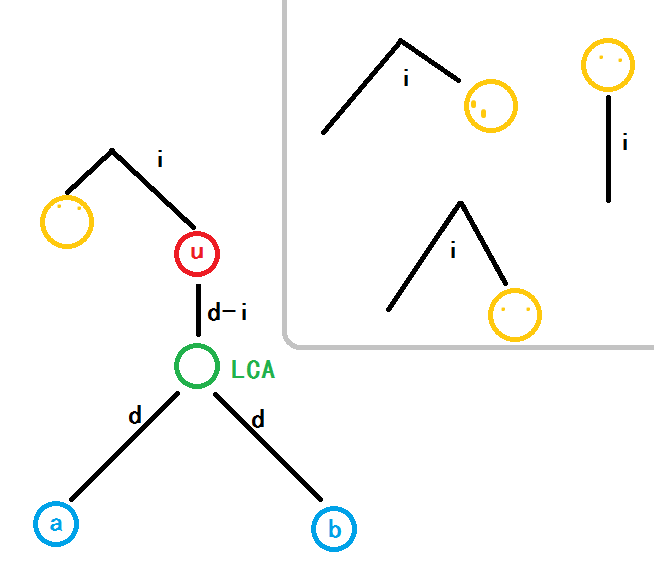
　　可以发现，三点对中，a和b这两个点已经确定，到LCA的长度都为d；而u到LCA这段要记录为d-i，实际上代表的是，u上面还要接一段长度为i的链 (d-i+i=d)，才能组成一个合法的三点对（a，b，和小黄点）。上图右框中都是符合的链，都可以接到u的上方，组成所求的三点对。

　　但是，d是不是还隐约存在于我们的定义之中呢......再看一幅图，实际上d是完全不存在的：

　　

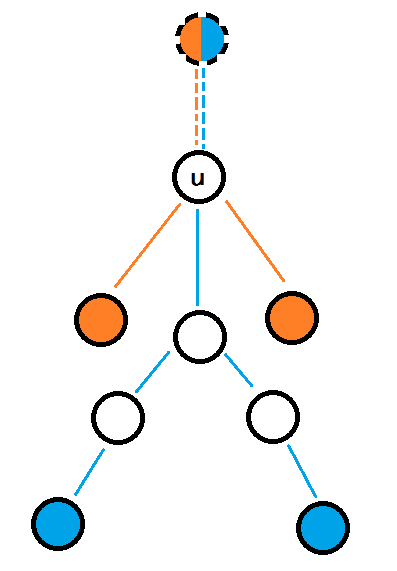
　　对于u这个点，$g [u][1]=2$，即满足$ g[u][1]$的点对数量为2。 因为不论是橙色的两个点还是蓝色的两个点，它们都可以通过在u上面连一条长为1的链，与链的另一端的节点组成完整的三点对。d不同的三点对，同样也能被记录入同一种状态。

　　于是我们就发现，g的定义完美地将最不稳定的因素d给省去了！

　　（搞定g是一个比较关键的步骤）

状态转移

　　现在我们看回f和g，稍加观察可以得出状态转移方程。

　　对于根节点为u的子树，记v为u的某一个儿子。我们先用当前u子树的统计信息与v的信息进行统计更新答案，随后将v合并入u子树的统计信息中。

1. 　　$Ans +=  \Sigma g [u][i]*f [v][i-1]  +  \Sigma g [v][i]*f [u][i-1]$
2. $g [u][i] += g [v][i+1] + f [u][i]*f [v][i-1] $
3. $f [u][i] += f [v][i-1]$

　　（以上的i-1或i+1，通过画图可以理解出来）

　　实现上，先递归儿子，返回时再更新与合并。

　　一定要注意边界问题！每个转移最好分开循环，以应对不同边界。（实在想不出请看代码）

　　时空复杂度$O(n^2)$

　   啥？

优化

　　我们采用长链剖分来优化转移。

　　考虑对于一个以u为根的子树，如果u只有一个儿子v，我们要怎么转移呢？

　　很显然很简单：

• $f [u][i]=f [v][i-1]$
• $g [u][i]=g [v][i+1]$

　　对于u的重儿子v，我们采用此方法直接通过指针O(1)转移；对于u的轻儿子（其他儿子），我们采用上方描述的方法进行暴力转移。

　　这样我们的时间复杂度就由$O(n^2)$降为了$O(n)$

　　空间呢？指针转移呢？

存储方式

　　　按说刚刚提到重儿子v直接$O(1)$转移的方式是指针，是因为我们发现有大量重复元素。对于一条重链上每个节点的f，我们发现父亲总是包含重儿子的信息；对于每个节点的g，我们发现重儿子的数组总是父亲数组向左偏移一位。

　　　现在，我们将$f [i][j]$映射到一维数组上（具体实现可以通过一个函数搞定，详细见代码的f(x,y)与g(x,y)，真正的一维数组是F和G）

　　　对于一条重链，若长度为len，那么我们可以只为这条重链申请长度为len的f数组空间，以及长度为2*len的g数组空间（因为每个节点的g数组都有len的大小，每次往左移动一位，最多移动len次）。这样f数组最大只会用到n，g数组最大只会用到2n，我们将空间复杂度降到了$O(n)$。

　　现在我们优先递归重儿子，从重儿子回溯后，就已经自动计算好了重儿子的答案啦，下面按照上面方法暴力合并其他子树即可。

　　特别地：从重儿子回溯的时候，需将$Ans+=g [u][0]$（$g [u][0]$即$g [重儿子][1]$），因为回溯的时候u充当了一个上端点，能与$g [重儿子][1]$组成答案（其实还不是全自动，是半自动......）。而从其他子树回溯的时候，上述状态转移方程可以覆盖这种情况。

　　总时间复杂度O(n)，空间复杂度O(n)。

 #include <bits/stdc++.h>
 typedef long long ll;
 using namespace std;
 const int N=;
 int n,tot,h[N];
 int dep[N],maxdep[N],son[N],top[N],stF[N],stG[N],posF,posG;
 ll F[N],G[N*],ans;
 struct Edge{int v,next;}eg[N*];
 inline void addEdge(int u,int v){
     eg[++tot].v=v; eg[tot].next=h[u]; h[u]=tot;
 }
 void preDfs(int u,int fa,int deep){
     dep[u]=maxdep[u]=deep;
     son[u]=-;
     for(int i=h[u],v;i;i=eg[i].next)
         if((v=eg[i].v)!=fa){
             preDfs(v,u,deep+);
             maxdep[u]=max(maxdep[u],maxdep[v]);
             if(son[u]==-||maxdep[v]>maxdep[son[u]])
                 son[u]=v;
         }
 }
 inline int f(int x,int y){return stF[top[x]]+dep[x]-dep[top[x]]+y;}
 inline int g(int x,int y){return stG[top[x]]-(dep[x]-dep[top[x]])+y;}
 inline int De(int u){return maxdep[u]-dep[u]+;}
 void dfs(int u,int fa,int Top){
     top[u]=Top;
     if(u==Top){
         stF[u]=posF;
         posF+=De(u);
         posG+=De(u)*;
         stG[u]=posG-De(u);
     }
     if(son[u]==-) return;
     dfs(son[u],u,Top);
     for(int i=h[u],v;i;i=eg[i].next)
         if((v=eg[i].v)!=fa&&v!=son[u])
             dfs(v,u,v);
 }
 void count(int u,int fa){
     F[f(u,)]=;
     if(son[u]!=-){
         count(son[u],u);
         ans+=G[g(u,)];
     }
     for(int I=h[u],v;I;I=eg[I].next){
         if((v=eg[I].v)!=fa&&v!=son[u]){
             count(v,u);
             for(int i=;i<=De(v);i++)
                 ans+=G[g(u,i)]*F[f(v,i-)];
             for(int i=;i<De(v);i++)
                 ans+=G[g(v,i)]*F[f(u,i-)];
             for(int i=;i<=De(v);i++)
                 G[g(u,i)]+=F[f(u,i)]*F[f(v,i-)];
             for(int i=;i<=De(v)-;i++)
                 G[g(u,i)]+=G[g(v,i+)];
             for(int i=;i<=De(v);i++)
                 F[f(u,i)]+=F[f(v,i-)];
         }
     }
 }
 inline void init(){
     tot=posF=posG=ans=;
     memset(h,,sizeof h);
     memset(F,,sizeof F);
     memset(G,,sizeof G);
 }
 int main(){
     while(){
         scanf("%d",&n);
         if(!n) break;
         init();
         for(int i=,x,y;i<n;i++)
             scanf("%d%d",&x,&y),
             addEdge(x,y), addEdge(y,x);
         preDfs(,,);
         dfs(,,);
         count(,);
         printf("%lld\n",ans);
     }
     return ;
 }

神奇代码