小白的Python之路 day4 迭代器

迭代器

学习前，我们回想一下可以直接作用于for循环的数据类型有以下几种：

　　1.集合数据类型，如list、tuple、dict、set、str等；

　　2.是generator，包括生成器和带yield的generator function。

这些可以直接作用于for循环的对象统称为可迭代对象：Iterable.(可迭代对象你可以简单的理解可循环的对象)

　　我们怎么判断一个对象是不是可循环或者可迭代的？

可以使用isinstance()判断一个对象是否是Iterable对象：  #isinstance()内置的方法

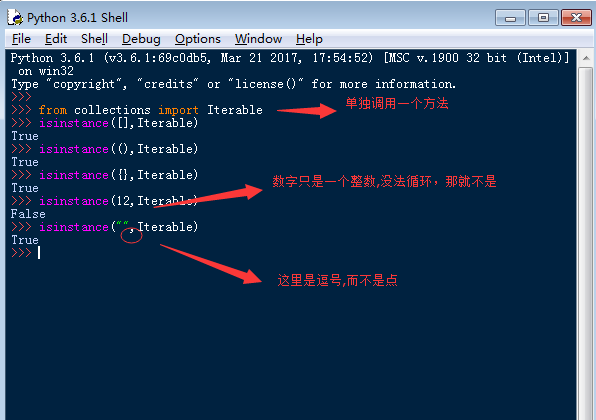
而生成器不但可以作用于for循环，还可以被next()函数不断调用并返回下一个值，直到最后抛出StopIteration错误表示无法继续返回下一个值了。

可以被next()函数调用并不断返回下一个值的对象称为迭代器：Iterator。

生成器一定是迭代器，而迭代器不一定是生成器(生成器有next方法，迭代器有next方法不一定是生成器)

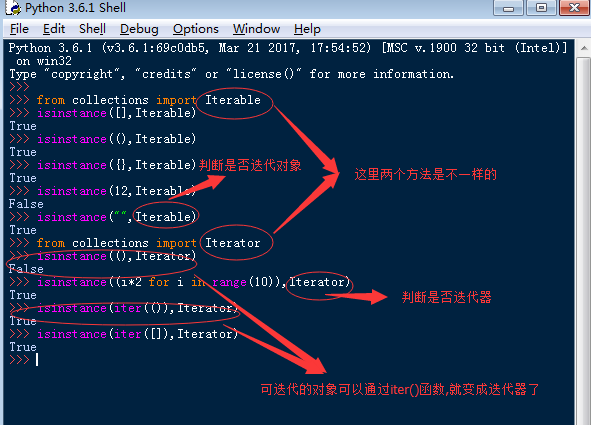
生成器都是Iterator对象，但list、dict、str虽然是Iterable，却不是Iterator。

把list、dict、str等Iterable变成Iterator可以使用iter()函数：

Python的Iterator对象表示的是一个数据流，Iterator对象可以被next()函数调用并不断返回下一个数据，直到没有数据时抛出StopIteration错误。可以把这个数据流看做是一个有序序列，但我们却不能提前知道序列的长度，只能不断通过next()函数实现按需计算下一个数据，所以Iterator的计算是惰性的(走到这一步，我才计算，不走到这一步，我就不计算)，只有在需要返回下一个数据时它才会计算。

Iterator甚至可以表示一个无限大的数据流，例如全体自然数。而使用list是永远不可能存储全体自然数的。

总结：

1.凡是可作用于for循环的对象都是Iterable类型；

2.凡是可作用于next()函数的对象都是Iterator类型，它们表示一个惰性计算的序列；

集合数据类型如list、dict、str等是Iterable但不是Iterator，不过可以通过iter()函数获得一个Iterator对象。

range()方法

在python2.7和python3的range()方法实现的原理是不一样的，下面我们就来用代码看看，代码如下：

1 2 3 4 5 6

>>> range(5)  #python2.7 [0, 1, 2, 3, 4] >>> xrange(5) #python2.7 xrange(5) >>> range(5)  #python3.5 range(0, 5)

从上面的代码可以看出，在python2.7中range()只是一个list，在python3中是一个迭代器，python2.7中xrange()跟python3中的range()功能是一样的。这就是为什么有同学会问python2.7中xrange()比range()方法更快， 

python3中的range()方法实现的原理如下：

1 2	for x in range(5):     pass

 实际相当于：range方法就是next()取的，只是封装了，我们看不到

1 2 3 4 5 6 7 8 9 10

# 首先获得Iterator对象: it = iter([1, 2, 3, 4, 5]) # 循环: while True:     try:         # 获得下一个值:         x = next(it)     except StopIteration:         # 遇到StopIteration就退出循环         break

在python 2.7 中,文件方法有f.xreadlines(),然后后面就可以用f.next()方法。在3.0中都一样被封装,了解一下就行，以后看到反正咱看得懂