Noip2016组合数（数论）

题目描述

组合数表示的是从n个物品中选出m个物品的方案数。举个例子，从（1,2,3) 三个物品中选择两个物品可以有（1,2),(1,3),(2,3)这三种选择方法。根据组合数的定 义，我们可以给出计算组合数的一般公式：

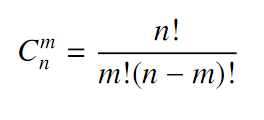
其中n! = 1 × 2 × · · · × n

小葱想知道如果给定n,m和k，对于所有的0 <= i <= n，0 <= j <= min(i,m)有多少对 (i,j)满足是k的倍数。

输入输出格式

输入格式：

第一行有两个整数t,k，其中t代表该测试点总共有多少组测试数据，k的意义见 【问题描述】。

接下来t行每行两个整数n,m，其中n,m的意义见【问题描述】。

输出格式：

t行，每行一个整数代表答案。

输入输出样例

输入样例#1：

1 2

3 3

输出样例#1：

1

输入样例#2：

2 5

4 5

6 7

输出样例#2：

0

7

说明

【样例1说明】

在所有可能的情况中，只有是2的倍数。

【子任务】

可以发现k是先给出的且不会变，想到先预处理出所有的答案

我们知道C(i,j)=C(i-1,j)+C(i-1,j-1),先用O(n^2)处理所有C[i][j]并取模

取b[i][j]表示c[i][j]是否能整除k,判断取模后是否为0即可

设f[i][[j]为对应的n=i,m=j的答案，分析f[i][j]的递推关系

其实打个表就容易找到规律，这里f[i][j]=C[i-1][j]+C[i][j-1]+C[i-1][j-1]+b[i][j]

代码如下，

#include <cstdio>
#include <cstring>
#define N 2020

int T, k, n, m;
int f[N][N];
bool b[N][N];

inline int read()
{
    int x = 0, f = 1; char ch = getchar();
    while (ch < '0' || ch > '9') {if (ch == '-')f = -1; ch = getchar();}
    while (ch >= '0' && ch <= '9') {x = x * 10 + ch - '0'; ch = getchar();}
    return x * f;
}

int main()
{
    T = read(), k = read();
    for (int i = 1; i <= N; ++i)
    {
        f[i][1] = i % k;
        f[i][i] = 1;
    }
    for (int i = 3; i <= 2000; ++i)
        for (int j = 2; j <= i - 1; ++j)
            f[i][j] = (f[i - 1][j] + f[i - 1][j - 1]) % k;
    for (int i = 1; i <= 2000; ++i)
        for (int j = 1; j <= i; ++j)
            if (!f[i][j]) b[i][j] = 1;
    memset(f, 0, sizeof(f));
    for (int i = 1; i <= 2000; ++i)
        for (int j = 1; j <= 2000; ++j)
            f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + b[i][j];
    while (T--)
    {
        n = read(), m = read();
        printf("%d\n", f[n][m]);
    }
    return 0;
}