HGOI20180822 五校联考卷

T1

【题目意思】给出下列程序片段，预测程序运行结果

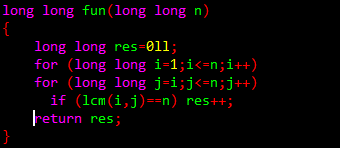
输入文件为T(T<=200)组数据,每组数据有个n(n<=10¹⁴)

输出文件为T行，每行一个数据，表示fun(n)的值

simple input：

simple output：

唯一分解定理可知：

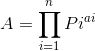
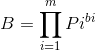
所以

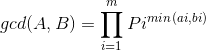
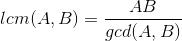
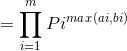
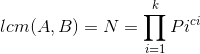
所以，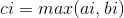  

深入分析发现首先ai和bi中必然有一个是ci而且另外一个的取值范围一定是[0，ci]之间

所以排列组合一下就是2ci+1种可能，对于每种可能的情况答案就是

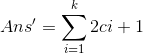
注意到程序只记录一遍而且存在平方数的存在，这样我们的答案就是这样

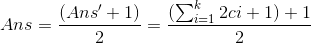
T2

【题目大意】 给出一个序列长度为n(n<=1000)有且仅有数字1-8组成，求出一个最长的子序列满足

1.子序列中相同元素排在一起

2.数字1-8各自出现的次数相差不多于1（最多相差1），没出现的按照0计算。

simple input：

simple output

# include<bits/stdc++.h>
using namespace std;
int f[][][];//f[前i个数字，每个最少出现个数，选取的状态]=最长子序列的长度
int a[],ans,n;
void dfs(int w,int v,int i)
{
    if (w==) {
        int lastv=v-(<<(-a[i]));
        int cnt=;
        for (int k=i-;k>=;k--)
        {
            f[i][cnt][v]=max(f[i][cnt][v],f[k][cnt][lastv]+cnt);
            f[i][cnt-][v]=max(f[i][cnt-][v],f[k][cnt-][lastv]+cnt);
            if (a[k]==a[i]) cnt++;
            if (cnt>) return;
        }
        return;
    }
    if (w!=a[i]) dfs(w+,v*,i);
    dfs(w+,v*+,i);
}
int main()
{
    scanf("%d",&n);
    memset(f,,sizeof(f));
    for (int i=;i<=n;i++) scanf("%d",&a[i]);
    for (int i=;i<=;i++) f[][][i]=;
    for (int i=;i<=;i++) f[][i][]=;
    for (int i=;i<=n;i++) {
        dfs(,,i);
        for (int j=;j<=;j++)
         ans=max(ans,f[i][j][]);
    }
    printf("%d\n",ans);
    return ;
 }