python 回溯法 子集树模板 系列 —— 9、旅行商问题（TSP）

问题

旅行商问题（Traveling Salesman Problem,TSP）是旅行商要到若干个城市旅行，各城市之间的费用是已知的，为了节省费用，旅行商决定从所在城市出发，到每个城市旅行一次后返回初始城市，问他应选择什么样的路线才能使所走的总费用最短？

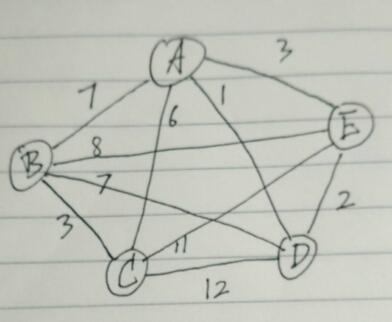
分析

此问题可描述如下：G=(V,E)是带权的有向图，找到包含V中每个结点一个有向环，亦即一条周游路线，使得这个有向环上所有边成本之和最小。

这个问题与前一篇文章的区别就是，本题是带权的图。只要一点小小的修改即可。

解的长度是固定的n+1。

对图中的每一个节点，都有自己的邻接节点。对某个节点而言，其所有的邻接节点构成这个节点的状态空间。当路径到达这个节点时，遍历其状态空间。

最终，一定可以找到最优解!

显然，继续套用回溯法子集树模板！！！

代码

'''旅行商问题（Traveling Salesman Problem,TSP）'''

# 用邻接表表示带权图
n = 5  # 节点数
a,b,c,d,e = range(n) # 节点名称
graph = [
    {b:7, c:6, d:1, e:3},
    {a:7, c:3, d:7, e:8},
    {a:6, b:3, d:12, e:11},
    {a:1, b:7, c:12, e:2},
    {a:3, b:8, c:11, d:2}
]

x = [0]*(n+1)  # 一个解（n+1元数组，长度固定）
X = []         # 一组解

best_x = [0]*(n+1)  # 已找到的最佳解（路径）
min_cost = 0        # 最小旅费

# 冲突检测
def conflict(k):
    global n,graph,x,best_x,min_cost

    # 第k个节点，是否前面已经走过
    if k < n and x[k] in x[:k]:
        return True

    # 回到出发节点
    if k == n and x[k] != x[0]:
        return True

    # 前面部分解的旅费之和超出已经找到的最小总旅费
    cost = sum([graph[node1][node2] for node1,node2 in zip(x[:k], x[1:k+1])])
    if 0 < min_cost < cost:
        return True

    return False # 无冲突

# 旅行商问题（TSP）
def tsp(k): # 到达（解x的）第k个节点
    global n,a,b,c,d,e,graph,x,X,min_cost,best_x

    if k > n: # 解的长度超出，已走遍n+1个节点 （若不回到出发节点，则 k==n）
        cost = sum([graph[node1][node2] for node1,node2 in zip(x[:-1], x[1:])]) # 计算总旅费
        if min_cost == 0 or cost < min_cost:
            best_x = x[:]
            min_cost = cost
            #print(x)
    else:
        for node in graph[x[k-1]]: # 遍历节点x[k-1]的邻接节点（状态空间）
            x[k] = node
            if not conflict(k): # 剪枝
                tsp(k+1)

# 测试
x[0] = c # 出发节点：路径x的第一个节点（随便哪个）
tsp(1)   # 开始处理解x中的第2个节点
print(best_x)
print(min_cost)

效果图