Verilog 加法器和减法器(6)

为了减小行波进位加法器中进位传播延迟的影响，可以尝试在每一级中快速计算进位，如果能在较短时间完成计算，则可以提高加法器性能。

我们可以进行如下的推导：

设 g_i=x_i&y_i, p_i = x_i +y _i

c_i+1 = x_i&y _i+x _i&c_i+y_i&c_i=x_i&y_i + (x_i+y_i)&c_i=g _i+p_i&c _i = g_i+p_i&(g_i-1+p_i-1&c_i-1)=g _i+p_i&g _i-1+pi&p_i-1&c_i-1= ….=g_i+p_i &g_i-1+p_i &p_i-1&g_i-2+…+p_i&p_i-1…p₂&p₁ &g₀+pi &p_i-1..p₁ &p₀&c₀; 实现这个逻辑电路的加法器是超前进位加法器。从公式中，可以看出门延时要比行波进位加法器小很多。但是电路复杂，逻辑门的扇入数量将限制超前进位加法器的速度。

由于扇入数量限制，通常我们仅实现4位超前进位加法器和8位超前进位加法器，然后在串联成16/32/64等高位加法器。

下面是4位和8位的超前进位加法器代码：

module adder4_fast(
                   cin,
                   x,
                   y,
                   s,
                   cout
                   );
 
input cin;
input [3:0] x;
input [3:0] y;
output [3:0] s;
output cout;
 
wire [4:0] g,p,c;
 
assign c[0] = cin;
assign p = x | y;
assign g = x & y;
//assign c[1] =  g[0] | (p[0] & c[0]);
//assign c[2] =  g[1] | (p[1] & (g[0] | (p[0] & c[0])));
//assign c[3] =  g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))));
//assign c[4] =  g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))))));
assign c[1] =  g[0] | (p[0] & c[0]);
assign c[2] =  g[1] | (p[1]&g[0])|(p[1]&p[0]&c[0]);
assign c[3] =  g[2] | (p[2]&g[1])|(p[2]&p[1]&g[0])|(p[2]&p[1]&p[0]&c[0]);
assign c[4] =  g[3] | (p[3]&g[2])|(p[3]&p[2]&g[1])|(p[3]&p[2]&p[1]&g[0])|(p[3]&p[2]&p[1]&p[0]&c[0]);
assign s = x^y^c[3:0];
assign cout = c[4];
 
endmodule

module adder8_fast(
                   cin,
                   x,
                   y,
                   s,
                   cout
                   );
 
input cin;
input [7:0] x;
input [7:0] y;
output [7:0] s;
output cout;
 
wire [8:0] g,p,c;
 
assign c[0] = cin;
assign p = x | y;
assign g = x & y;
//assign c[1] =  g[0] | (p[0] & c[0]);
//assign c[2] =  g[1] | (p[1] & (g[0] | (p[0] & c[0])));
//assign c[3] =  g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))));
//assign c[4] =  g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))))));
//assign c[5] =  g[4] | (p[4] & (g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))))))));
//assign c[6] =  g[5] | (p[5] & (g[4] | (p[4] & (g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))))))))));
//assign c[7] =  g[6] | (p[6] & (g[5] | (p[5] & (g[4] | (p[4] & (g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))))))))))));
//assign c[8] =  g[7] | (p[7] & (g[6] | (p[6] & (g[5] | (p[5] & (g[4] | (p[4] & (g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))))))))))))));
assign c[1] =  g[0] | (p[0] & c[0]);
assign c[2] =  g[1] | (p[1]&g[0])|(p[1]&p[0]&c[0]);
assign c[3] =  g[2] | (p[2]&g[1])|(p[2]&p[1]&g[0])|(p[2]&p[1]&p[0]&c[0]);
assign c[4] =  g[3] | (p[3]&g[2])|(p[3]&p[2]&g[1])|(p[3]&p[2]&p[1]&g[0])|(p[3]&p[2]&p[1]&p[0]&c[0]);
assign c[5] =  g[4] | (p[4]&g[3])|(p[4]&p[3]&g[2])|(p[4]&p[3]&p[2]&g[1])|(p[4]&p[3]&p[2]&p[1]&g[0])|(p[4]&p[3]&p[2]&p[1]&p[0]&c[0]);
assign c[6] =  g[5] | (p[5]&g[4])|(p[5]&p[4]&g[3])|(p[5]&p[4]&p[3]&g[2])|(p[5]&p[4]&p[3]&p[2]&g[1])|(p[5]&p[4]&p[3]&p[2]&p[1]&g[0])|(p[5]&p[4]&p[3]&p[2]&p[1]&p[0]&c[0]);
assign c[7] =  g[6] | (p[6]&g[5])|(p[6]&p[5]&g[4])|(p[6]&p[5]&p[4]&g[3])|(p[6]&p[5]&p[4]&p[3]&g[2])|(p[6]&p[5]&p[4]&p[3]&p[2]&g[1])|(p[6]&p[5]&p[4]&p[3]&p[2]&p[1]&g[0])|(p[6]&p[5]&p[4]&p[3]&p[2]&p[1]&p[0]&c[0]);
assign c[8] =  g[7] | (p[7]&g[6])|(p[7]&p[6]&g[5])|(p[7]&p[6]&p[5]&g[4])|(p[7]&p[6]&p[5]&p[4]&g[3])|(p[7]&p[6]&p[5]&p[4]&p[3]&g[2])|(p[7]&p[6]&p[5]&p[4]&p[3]&p[2]&g[1])|(p[7]&p[6]&p[5]&p[4]&p[3]&p[2]&p[1]&g[0])|(p[7]&p[6]&p[5]&p[4]&p[3]&p[2]&p[1]&p[0]&c[0]);
assign s = x^y^c[7:0];
assign cout = c[8];
 
endmodule

下面的代码把4个超前进位加法器串联起来，形成一个32位加法器。

module addern_fast(
                   cin,
                   x,
                   y,
                   s,
                   cout
                   );
 
input cin;
input [31:0] x;
input [31:0] y;
output [31:0] s;
output cout;
wire [2:0] cout_tmp;
 
adder8_fast adder8_fast_0(.cin(cin),.x(x[7:0]),.y(y[7:0]),.s(s[7:0]),.cout(cout_tmp[0]));
adder8_fast adder8_fast_1(.cin(cout_tmp[0]),.x(x[15:8]),.y(y[15:8]),.s(s[15:8]),.cout(cout_tmp[1]));
adder8_fast adder8_fast_2(.cin(cout_tmp[1]),.x(x[23:16]),.y(y[23:16]),.s(s[23:16]),.cout(cout_tmp[2]));
adder8_fast adder8_fast_3(.cin(cout_tmp[2]),.x(x[31:24]),.y(y[31:24]),.s(s[31:24]),.cout(cout));
 
endmodule

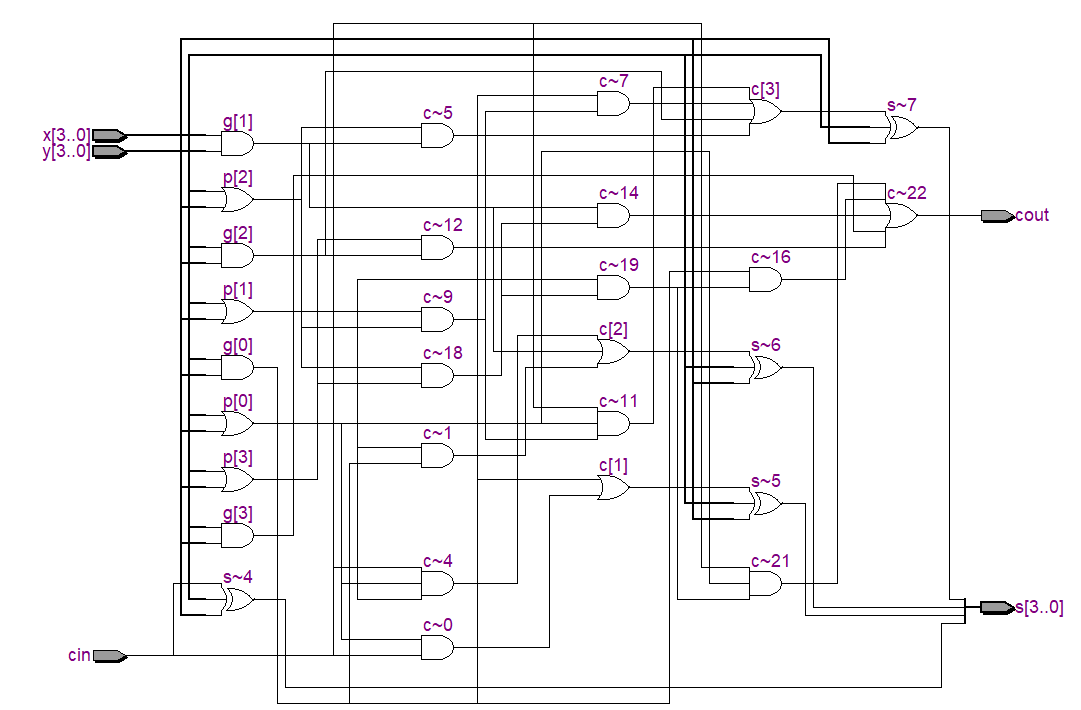
下面是4位超前进位加法器的逻辑图：

8位超前进位加法器的波形结果。