PBR Step by Step（四）Lambertian反射模型

光照可分为局部光照和全局光照。

局部光照：直接照射到物体表面的光照

全局光照：物体表面受周围环境影响的光照

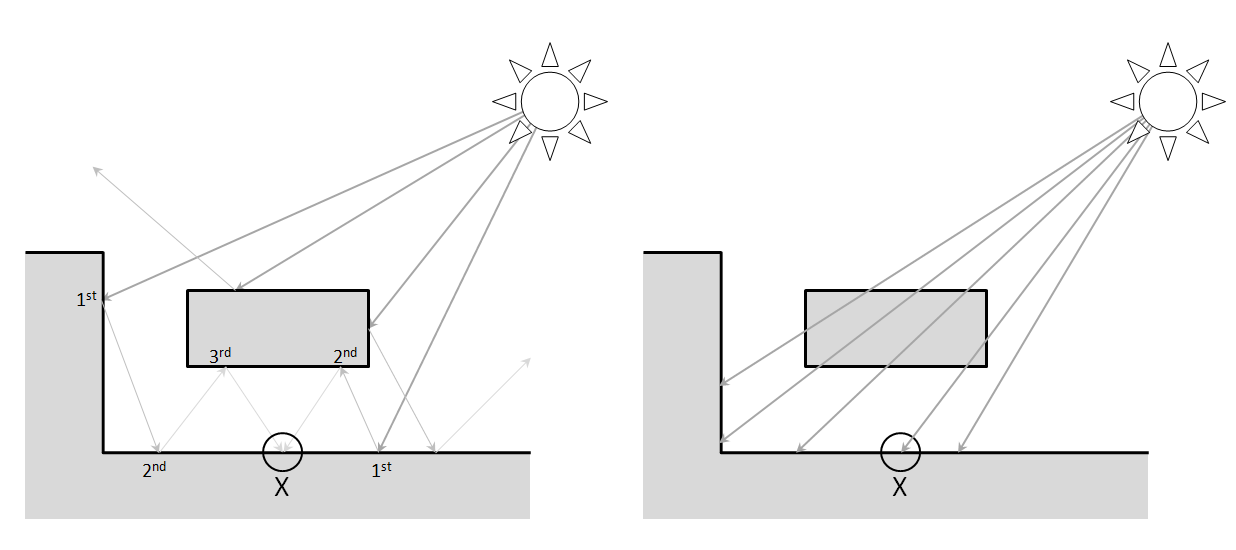
左图中点x接收到周围环境的光线照射，来自周围表面的反射光照称为全局光照；右图中点x接收来自太阳光的直接照射，来自太阳发射的直接光照称为局部光照。

在现实环境中，全局光照的情况更为复杂，例如：

• 半透明表面（Semi-transparent surfaces）：光线可以穿过表面进行复杂的交互，如玻璃棱镜，可以改变光的波长；
• 次表面散射（Sub-Surface Scattering）：光线可以穿过子表面，在同一表面的不同方向反射，如皮肤；
• 表面渗色（Surface bleeding）：光线穿过表面，在介质中改变颜色到目标表面。

其他例子还有很多，全局光照会比局部光照效果更佳柔和自然，但考虑到其复杂性，应用到实时渲染中也是有一定难度的。

我们在前几篇中通过理论得到的BRDF光照模型公式实际为局部光照模型中，还欠缺了全局光照因素。

下面，我们来研究一下BRDF的局部反射模型，先来看下最简单的Lambertian反射模型。

Lambertian反射模型

Lambertian反射称作完全漫反射。这是一种理想情况，现实中不存在完全漫反射，但Lambertian可以用来近似的模拟一些粗糙表面的效果，比如纸张。

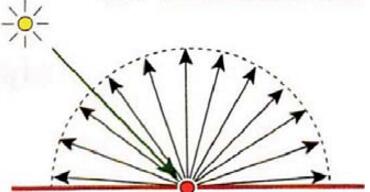
对于Lambertian表面，入射方向与出射方向无关，\({\omega_i}\)与\({\omega_o}\)无关，\({L_o(p, \omega_o)}\)可以表示为\({L_o(p, \omega_o)} = {L_r(p)}\)。

在上一篇中，我们知道反射辐射度的方程为：

\({L_o(p,\omega_o)} = \int_{\Omega_i}{f_r(p, \omega_i, \omega_o)}\, {L_i(p, \omega_i)}\, {\cos \theta_i}\, {d\omega_i}\)

在Lambertian反射模型中，由于\({\omega_i}\)与\({\omega_o}\)无关，BRDF项\({f_r(p, \omega_i, \omega_o)} = {f_r(p)}\)，上式可表示为：

\({L_r(p)} = {f_r(p)\int_{\Omega_i}L_i(p, \omega_i)\, \cos \theta_i \, d\omega_i} = {f_r(p)\, E_i(p)}\)

\(\Rightarrow {f_r(p)} = \frac{L_r(p)}{E_i(p)}\)

在上一篇的反射率中，\({\Omega_o}\)内的反射通量\({d\Phi_o} = {dA\int_{\Omega_o}L_o(p,\omega_o) \, \cos \theta_o \, d\omega_o}\)

在整个Lambertian表面半球积分（\({\Omega_o} = {2\pi}\)）中:

\({d\Phi_o} = {dAL_r(p)\int_{2\pi}\cos \theta_o \, d\omega_o} = {dA \, L_r(p) \, \pi}\)

式中的\({\int_{2\pi}\cos \theta_o \, d\omega_o} = {\pi}\)，这是一个半球积分，在第一篇中我们推出过该结果。

\({d\Phi_i} = {dA\int_{2\pi} L_i(p, \omega_i) \, \cos \theta_i \, d\omega_i} = {dA \, E_i(p)}\)

反射率\({\rho_d(p)} = \frac{d\phi_o}{d\phi_i} = \frac{L_r(p) \, \pi}{E_i(p)} = {f_r(p) \, \pi}\)

这样，我们就得到了Lambertain BRDF：\({f_r(p)} = \frac{\rho_d(p)}{\pi}\)

其中\({\rho_d}\)可以用常数项表示：\({\rho_d} = {k_d \, c_d}\)，\({k_d \in [0, 1]}\)，表示漫反射系数；\({c_d}\)表示漫反射颜色。

Lambertain BRDF又可写为\({f_r(p)} = \frac{k_d \, c_d}{\pi}\)

我们通常在实时渲染出于性能方面的考虑，会省略掉\(\pi\)，我们熟知的漫反射颜色计算公式，就是从反射辐射度方程中简化而来的：

反射辐射度方程：\({L_o(p,\omega_o)} = {f_r(p, \omega_i, \omega_o)}\int_{\Omega_i}{L_i(p, \omega_i)}\, {\cos \theta_i}\, {d\omega_i}\)

漫反射着色公式：\({L_r} = {k_d \, c_d} {\sum_{1}^{n}  \, L_i \, (n * l)} \)

对比看一下，是不是很像？\(\sum_{1}^{n}\)表示逐个光源求和近似积分，\({L_i}\)表示光源强度，\({n * l}\)表示\({\cos \theta_i}\)项