Codeforces Round #306 (Div. 2)

A. Two Substrings

You are given string s. Your task is to determine if the given string s contains two non-overlapping substrings "AB" and "BA" (the substrings can go in any order).

Input

The only line of input contains a string s of length between 1 and 105 consisting of uppercase Latin letters.

Output

Print "YES" (without the quotes), if string s contains two non-overlapping substrings "AB" and "BA", and "NO" otherwise.

Sample test(s)

input

ABA

output

NO

input

BACFAB

output

YES

input

AXBYBXA

output

NO

Note

In the first sample test, despite the fact that there are substrings "AB" and "BA", their occurrences overlap, so the answer is "NO".

In the second sample test there are the following occurrences of the substrings: BACFAB.

In the third sample test there is no substring "AB" nor substring "BA".

注意细节、比如：ABACAB

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
#define N 100010

int main()
{
    char s[N];
    char s1[]="AB",s2[]="BA";
    while(scanf("%s",s)!=EOF)
    {
        bool flag=;
        int len=strlen(s);
        if(len<=) flag=;
        else{
            char *p=strstr(s,s1);
            char *q=strstr(s,s2);
            if(p==NULL || q==NULL) flag=;
            else{
                if(strstr(p+,s2) || strstr(q+,s1)) ;
                else flag=;
            }
        }
        if(!flag) cout<<"NO\n";
        else cout<<"YES\n";
    }
    return ;
}

B. Preparing Olympiad

You have n problems. You have estimated the difficulty of the i-th one as integer ci. Now you want to prepare a problemset for a contest, using some of the problems you've made.

A problemset for the contest must consist of at least two problems. You think that the total difficulty of the problems of the contest must be at least l and at most r. Also, you think that the difference between difficulties of the easiest and the hardest of the chosen problems must be at least x.

Find the number of ways to choose a problemset for the contest.

Input

The first line contains four integers n, l, r, x (1 ≤ n ≤ 15, 1 ≤ l ≤ r ≤ 109, 1 ≤ x ≤ 106) — the number of problems you have, the minimum and maximum value of total difficulty of the problemset and the minimum difference in difficulty between the hardest problem in the pack and the easiest one, respectively.

The second line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 106) — the difficulty of each problem.

Output

Print the number of ways to choose a suitable problemset for the contest.

Sample test(s)

input

3 5 6 1
1 2 3

output

2

input

4 40 50 10
10 20 30 25

output

2

input

5 25 35 10
10 10 20 10 20

output

6

Note

In the first example two sets are suitable, one consisting of the second and third problem, another one consisting of all three problems.

In the second example, two sets of problems are suitable — the set of problems with difficulties 10 and 30 as well as the set of problems with difficulties 20 and 30.

In the third example any set consisting of one problem of difficulty 10 and one problem of difficulty 20 is suitable.

暴力即可

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
#define INF 1<<30
#define N 50

int ans;
int n,l,r,x;
int c[N];

void dfs(int id,int sum,int mx,int mi,int num){
    if(id>n){
        if(sum>=l&&sum<=r&&num>=&&mx-mi>=x)ans++;
        return;
    }
    dfs(id+,sum+c[id],max(mx,c[id]),min(mi,c[id]),num+);
    dfs(id+,sum,mx,mi,num);
}
int main()
{
    ans=;
    cin>>n>>l>>r>>x;
    for(int i=;i<=n;++i)cin>>c[i];
    dfs(,,,INF,);
    cout<<ans<<endl;
    return ;
}

C. Divisibility by Eight

You are given a non-negative integer n, its decimal representation consists of at most 100 digits and doesn't contain leading zeroes.

Your task is to determine if it is possible in this case to remove some of the digits (possibly not remove any digit at all) so that the result contains at least one digit, forms a non-negative integer, doesn't have leading zeroes and is divisible by 8. After the removing, it is forbidden to rearrange the digits.

If a solution exists, you should print it.

Input

The single line of the input contains a non-negative integer n. The representation of number n doesn't contain any leading zeroes and its length doesn't exceed 100 digits.

Output

Print "NO" (without quotes), if there is no such way to remove some digits from number n.

Otherwise, print "YES" in the first line and the resulting number after removing digits from number n in the second line. The printed number must be divisible by 8.

If there are multiple possible answers, you may print any of them.

Sample test(s)

input

3454

output

YES
344

input

10

output

YES
0

input

111111

output

NO

一个数是8的倍数,那么该数模1000得到的最后三位组成的数字一定是8的倍数
所以暴力枚举最后三位即可

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
using namespace std;
#define INF 0x7fffffff
#define N 110

char s[N];
int num[N];

int main()
{
    scanf("%s", s);
    int len = strlen(s);
    for (int i = ; i < len; i++) num[i] = s[i] - '';
    //
    for (int i = ; i < len; i++) {
        if (num[i] %  == ) {
            printf("YES\n");
            printf("%d\n", num[i]);
            return ;
        }
    }
    //
    for (int i = ; i < len; i++) {
        for (int j = i + ; j < len; j++) {
            int sum = num[i] *  + num[j];
            if (sum %  == ) {
                printf("YES\n");
                printf("%d\n", sum);
                return ;
            }
        }
    }
    //3+
    if (len >= ) {
        for (int  i = ; i < len; i++) {
            for (int j = i + ; j < len; j++) {
                for (int k = j + ; k < len; k++) {
                    int sum = num[i] *  + num[j] *  + num[k];
                    if (sum %  == ) {
                        printf("YES\n");
                        printf("%d\n", sum);
                        return ;
                    }
                }
            }
        }
    }
    printf("NO\n");
    return ;
}

D. Regular Bridge

An undirected graph is called k-regular, if the degrees of all its vertices are equal k. An edge of a connected graph is called a bridge, if after removing it the graph is being split into two connected components.

Build a connected undirected k-regular graph containing at least one bridge, or else state that such graph doesn't exist.

Input

The single line of the input contains integer k (1 ≤ k ≤ 100) — the required degree of the vertices of the regular graph.

Output

Print "NO" (without quotes), if such graph doesn't exist.

Otherwise, print "YES" in the first line and the description of any suitable graph in the next lines.

The description of the made graph must start with numbers n and m — the number of vertices and edges respectively.

Each of the next m lines must contain two integers, a and b (1 ≤ a, b ≤ n, a ≠ b), that mean that there is an edge connecting the vertices a and b. A graph shouldn't contain multiple edges and edges that lead from a vertex to itself. A graph must be connected, the degrees of all vertices of the graph must be equal k. At least one edge of the graph must be a bridge. You can print the edges of the graph in any order. You can print the ends of each edge in any order.

The constructed graph must contain at most 106 vertices and 106 edges (it is guaranteed that if at least one graph that meets the requirements exists, then there also exists the graph with at most 106 vertices and at most 106 edges).

Sample test(s)

input

1

output

YES
2 1
1 2

Note

In the sample from the statement there is a suitable graph consisting of two vertices, connected by a single edge.

求至少有一个桥的K-正则图。

如图，可以看出偶数无解、代码略(hen)搓

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
using namespace std;
#define INF 0x7fffffff
#define N 110

int main()
{
    int k;
    while(scanf("%d",&k)!=EOF)
    {
        if(k%==) printf("NO\n");
        else
        {
            printf("YES\n");
            if(k==)
            {
                printf("2 1\n");
                printf("1 2\n");
                continue;
            }
            int s1=,s2=*k;
            printf("%d %d\n",*k-,*(k-)+*(k-)*(k-)+(k-)+);
            printf("%d %d\n",s1,s2);
            for(int i=s1+;i<s1+k;i++) printf("%d %d\n",s1,i);
            for(int i=s1+;i<s1+k;i++){
                for(int j=s1+k;j<s1+*k-;j++){
                    printf("%d %d\n",i,j);
                }
            }
            for(int i=s1+k;i<s1+*k-;i+=) printf("%d %d\n",i,i+);
            for(int i=s2+;i<s2+k;i++) printf("%d %d\n",s2,i);
            for(int i=s2+;i<s2+k;i++){
                for(int j=s2+k;j<s2+*k-;j++){
                    printf("%d %d\n",i,j);
                }
            }
            for(int i=s2+k;i<s2+*k-;i+=) printf("%d %d\n",i,i+);
        }
    }
    return ;
}

E. Brackets in Implications

Implication is a function of two logical arguments, its value is false if and only if the value of the first argument is true and the value of the second argument is false.

Implication is written by using character '', and the arguments and the result of the implication are written as '0' (false) and '1' (true). According to the definition of the implication:

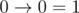
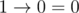
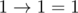
When a logical expression contains multiple implications, then when there are no brackets, it will be calculated from left to fight. For example,

.

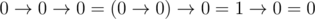When there are brackets, we first calculate the expression in brackets. For example,

.

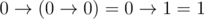For the given logical expression 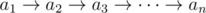 determine if it is possible to place there brackets so that the value of a logical expression is false. If it is possible, your task is to find such an arrangement of brackets.

Input

The first line contains integer n (1 ≤ n ≤ 100 000) — the number of arguments in a logical expression.

The second line contains n numbers a1, a2, ..., an (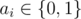), which means the values of arguments in the expression in the order they occur.

Output

Print "NO" (without the quotes), if it is impossible to place brackets in the expression so that its value was equal to 0.

Otherwise, print "YES" in the first line and the logical expression with the required arrangement of brackets in the second line.

The expression should only contain characters '0', '1', '-' (character with ASCII code 45), '>' (character with ASCII code 62), '(' and ')'. Characters '-' and '>' can occur in an expression only paired like that: ("->") and represent implication. The total number of logical arguments (i.e. digits '0' and '1') in the expression must be equal to n. The order in which the digits follow in the expression from left to right must coincide with a1, a2, ..., an.

The expression should be correct. More formally, a correct expression is determined as follows:

• Expressions "0", "1" (without the quotes) are correct.
• If v1, v2 are correct, then v1->v2 is a correct expression.
• If v is a correct expression, then (v) is a correct expression.

The total number of characters in the resulting expression mustn't exceed 106.

If there are multiple possible answers, you are allowed to print any of them.

Sample test(s)

input

4
0 1 1 0

output

YES
(((0)->1)->(1->0))

input

2
1 1

output

NO

input

1
0

output

YES
0

显然末尾必须为0
那么如果能这样：0/1 -> 1 ->0 = 0，就一定行
分为两种情况：
A. 如果a[n-1]本身就是1，那么显然可以
B. 如果a[n-1]为0,那么前面的1和0运算得到0,需要前面有1一个0来让0变成1
比如：1 0 1 1 1 0 0 ：1->(0->(1->(1->(1->0))))->0

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
#define N 100010

int main()
{
    int a[N],n;
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=;i<=n;i++) scanf("%d",&a[i]);
        if(a[n]){
            printf("NO\n");
            continue;
        }
        //
        if(n==)
        {
            printf("YES\n");
            printf("0\n");
        }
        //
        else if(n==)
        {
            if(a[]){
                printf("YES\n");
                printf("1->0\n");
            }
            else{
                printf("NO\n");
            }
        }
        //3+
        else{
            if(a[n-]){
                printf("YES\n");
                for(int i=;i<=n-;i++) printf("%d->",a[i]);
                printf("%d",a[n]);
            }
            else{
                int fg=-;
                for(int i=n-;i>=;i--) if(!a[i]) {fg=i;break;}
                if(fg==-) {printf("NO\n");continue;}
                printf("YES\n");
                for(int i=;i<fg;i++) printf("%d->",a[i]);
                for(int i=fg;i<=n-;i++) printf("(%d->",a[i]);
                printf("%d",a[n-]);
                for(int i=fg;i<=n-;i++) printf(")");
                printf("->%d\n",);
            }
        }
    }
    return ;
}