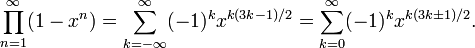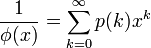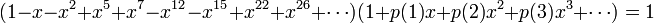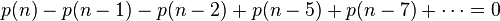2013 Multi-University Training Contest 5 Partition
思路:五边形数定理!!!
五边形数定理是一个由欧拉发现的数学定理,描述欧拉函数展开式的特性。欧拉函数的展开式如下:
亦即
欧拉函数展开后,有些次方项被消去,只留下次方项为1, 2, 5, 7, 12, ...的项次,留下来的次方恰为广义五边形数。
若将上式视为幂级数,其收敛半径为1,不过若只是当作形式幂级数(formal power series)来考虑,就不会考虑其收敛半径。
欧拉函数的倒数是分割函数的母函数,亦即:
其中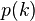 为k的分割函数。
为k的分割函数。
上式配合五边形数定理,可以得到
考虑 项的系数,在 n>0 时,等式右侧的系数均为0,比较等式二侧的系数,可得
项的系数,在 n>0 时,等式右侧的系数均为0,比较等式二侧的系数,可得
因此可得到分割函数p(n)的递归式
以n=10为例
这就是所求的了,当n<0时,p(n)=0;
p(n)的其他性质:
当限定将 表示成刚好
表示成刚好 个正整数之和时,可以表示为
个正整数之和时,可以表示为 。显然,
。显然, 。
。
- 对于
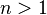 ,
,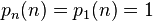
 (OEIS:A004526)
(OEIS:A004526)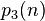 = 最接近
= 最接近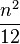 的正整数。(OEIS:A069905)
的正整数。(OEIS:A069905)
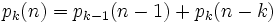
代码如下:
#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<iomanip>
#include<cmath>
#include<string>
#include<vector>
#define ll __int64
#define pi acos(-1.0)
#define MAX 100001
using namespace std;
const int mod=;
int an[MAX],n,t;
void init(){
int i,j;
an[]=an[]=;
an[]=;an[]=;an[]=;
an[]=;
for(i=;i<MAX;i++){
an[i]=;
for(j=;;j++){
int g=j*(*j-)/;
if(i-g<) break;
if(j&) an[i]+=an[i-g];
else an[i]-=an[i-g];
an[i]=an[i]%mod;
while(an[i]<) an[i]+=mod;
g=j*(*j+)/;
if(i-g<) break;
if(j&) an[i]+=an[i-g];
else an[i]-=an[i-g];
an[i]=an[i]%mod;
while(an[i]<) an[i]+=mod;
}
an[i]%=mod;
}
}
int main(){
init();
scanf("%d",&t);
while(t--){
scanf("%d",&n);
printf("%d\n",an[n]);
}
return ;
}
2013 Multi-University Training Contest 5 Partition的更多相关文章
- 2013 Multi-University Training Contest 1 Partition
这题主要是推公式…… ;}
- Integer Partition(hdu4658)2013 Multi-University Training Contest 6 整数拆分二
Integer Partition Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) T ...
- Partition(hdu4651)2013 Multi-University Training Contest 5
Partition Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Sub ...
- Partition(hdu4651)2013 Multi-University Training Contest 5----(整数拆分一)
Partition Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Sub ...
- ACM ICPC Central Europe Regional Contest 2013 Jagiellonian University Kraków
ACM ICPC Central Europe Regional Contest 2013 Jagiellonian University Kraków Problem A: Rubik’s Rect ...
- HDU 2018 Multi-University Training Contest 1 Triangle Partition 【YY】
传送门:http://acm.hdu.edu.cn/showproblem.php?pid=6300 Triangle Partition Time Limit: 2000/1000 MS (Java ...
- JSU 2013 Summer Individual Ranking Contest - 5
JSU 2013 Summer Individual Ranking Contest - 5 密码:本套题选题权归JSU所有,需要密码请联系(http://blog.csdn.net/yew1eb). ...
- HDU4888 Redraw Beautiful Drawings(2014 Multi-University Training Contest 3)
Redraw Beautiful Drawings Time Limit: 3000/1500 MS (Java/Others) Memory Limit: 65536/65536 K (Jav ...
- HDU 2018 Multi-University Training Contest 3 Problem A. Ascending Rating 【单调队列优化】
任意门:http://acm.hdu.edu.cn/showproblem.php?pid=6319 Problem A. Ascending Rating Time Limit: 10000/500 ...
随机推荐
- jQuery 自定义事件的学习笔记
jquery中提供了两种方法可以绑定自定义事件: bind()和one()而绑定的自定义事件的触发,必须得用jquery中的trigger()方法才能触发. 我们先来看on事件 代码如下 复制代码 ...
- KVC/KVO总结
KVC(键值编码) 动态设置: setValue:属性值 forKey:属性名(用于简单路径) setValue:属性值 forKeyPath:属(用于复合路径,例如Person有一个Account类 ...
- 给label text 上色 && 给textfiled placeholder 上色
1.给label text 上色: NSInteger stringLength = ; stringLength = model.ToUserNickName.length; NSMutableAt ...
- Windows7下安装搭建redis教程和配置详解
作者:Sungeek 出处:http://www.cnblogs.com/Sungeek/ 欢迎转载,也请保留这段声明.谢谢! 简介: Redis是一个开源的使用ANSI C语言编写.支持网络.可基于 ...
- 【转】404、500、502等HTTP状态码介绍
基本涵盖了所有问题HTTP 400 – 请求无效HTTP 401.1 – 未授权:登录失败HTTP 401.2 – 未授权:服务器配置问题导致登录失败HTTP 401.3 – ACL 禁止访问资源HT ...
- 算法 fill
fill(vec.begin(), vec.end(),); //reset all elements to fill(vec.begin(),vec.begin + vec.size/, );//s ...
- C++对象的JSON序列化与反序列化探索续-复杂对象的序列化与反序列化
本文是基本上一篇博文进行改进而成,上一篇请见: C++对象的JSON序列化与反序列化探索 此处就不多说了,直接上代码. 1. 序列化基类 #pragma once #include <strin ...
- Java使用基本JDK操作ZIP文件以及zip文件的加密、解密等功能
Java使用基本JDK操作ZIP文件 http://blog.csdn.net/zhyh1986/article/details/7723649 Java解压和压缩带密码的zip文件 http://b ...
- Jquery 控件
1. Jeditable 2. Select2 3. superfish 4. Jquery file upload https://blueimp.github.io/jQuery-File-Upl ...
- 【转】 设定linux 系统可用资源
getrlimit和setrlimit函数 每个进程都有一组资源限制,其中某一些可以用getrlimit和setrlimit函数查询和更改. #include #include int getrli ...