B+树概念学习

转载自 从B树、B+树、B*树谈到R 树

1.用阶定义的B树

B 树又叫平衡多路查找树。一棵m阶的B 树 (注：切勿简单的认为一棵m阶的B树是m叉树，虽然存在四叉树，八叉树，KD树，及vp/R树/R*树/R+树/X树/M树/线段树/希尔伯特R树/优先R树等空间划分树，但与B树完全不等同)的特性如下：

1. 树中每个结点最多含有m个孩子（m>=2）；
2. 除根结点和叶子结点外，其它每个结点至少有[ceil(m / 2)]个孩子（其中ceil(x)是一个取上限的函数）；
3. 若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；
4. 所有叶子结点都出现在同一层，叶子节点没有孩子和指向孩子的指针，这些节点也存在，也有元素。

每个非终端结点中包含有n个关键字信息： (n，P0，K1，P1，K2，P2，......，Kn，Pn)。其中：
       a)   Ki (i=1...n)为关键字，且关键字按顺序升序排序K(i-1)< Ki。 
       b)   Pi为指向子树根的接点，且指针P(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。 
       c)   关键字的个数n必须满足： [ceil(m / 2)-1]<= n <= m-1。

 

例1：

 

    如上图所示，即是一棵B树，一棵关键字为英语中辅音字母的B树，现在要从树种查找字母R（包含n[x]个关键字的内结点x，x有n[x]+1]个子女（也就是说，一个内结点x若含有n[x]个关键字，那么x将含有n[x]+1个子女）。所有的叶结点都处于相同的深度，带阴影的结点为查找字母R时要检查的结点）：

相信，从上图你能轻易的看到，一个内结点x若含有n[x]个关键字，那么x将含有n[x]+1个子女。如含有2个关键字D H的内结点有3个子女，而含有3个关键字Q T X的内结点有4个子女。

 

 

例2：一棵包含24个英文字母的5阶B树的存储结构图。

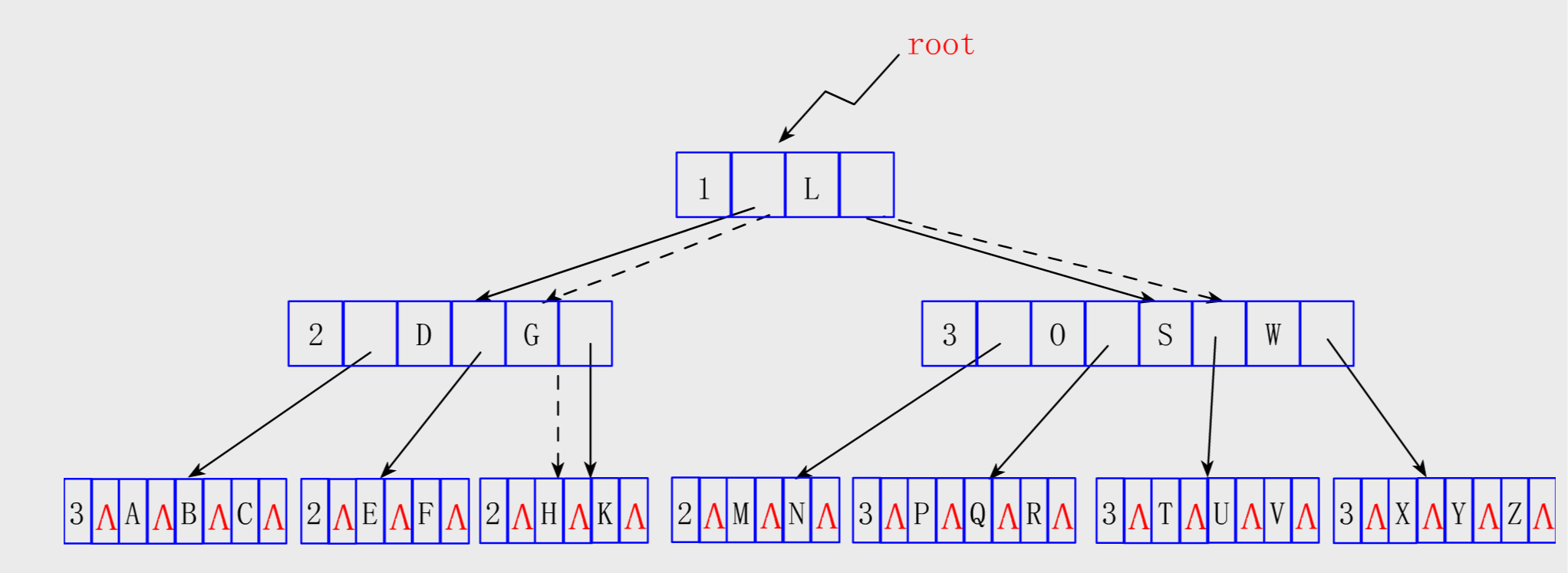
说明：
　    按照定义，在5【m】阶B树里，根中的关键字数目可以是1～4，子树数可以是2～5；其它的结点中关键字数目可以是2～4【 [ceil(m / 2)-1]<= n <= m-1】，若该结点不是叶子，则它可以有3～5棵子树【[ceil(m / 2)]<=n<=m】。

2.B树的高度

若B树某一非叶子节点包含N个关键字，则此非叶子节点含有N+1个孩子结点，而所有的叶子结点都在第I层，我们可以得出：

1. 因为根至少有两个孩子，因此第2层至少有两个结点。
2. 除根和叶子外，其它结点至少有┌m/2┐个孩子，
3. 因此在第3层至少有2*┌m/2┐个结点，
4. 在第4层至少有2*(┌m/2┐^2)个结点，
5. 在第 I 层至少有2*(┌m/2┐^(l-2) )个结点，于是有： N+1 ≥ 2*┌m/2┐I-2；
6. 考虑第L层的结点个数为N+1，那么2*(┌m/2┐^(l-2)）≤N+1，也就是L层的最少结点数刚好达到N+1个，即： I≤ log┌m/2┐((N+1)/2 )+2；

 

　　所以

• 当B树包含N个关键字时，B树的最大高度为l-1（因为计算B树高度时，叶结点所在层不计算在内），即：l - 1 = log┌m/2┐((N+1)/2 )+1。

 

　　这个B树的高度公式从侧面显示了B树的查找效率是相当高的。

曾在一次面试中被问到，一棵含有N个总关键字数的m阶的B树的最大高度是多少?答曰：log_ceil（m/2）(N+1)/2 + 1 （上面中关于m阶B树的第1点特性已经提到：树中每个结点含有最多含有m个孩子，即m满足：ceil(m/2)<=m<=m。而树中每个结点含孩子数越少，树的高度则越大，故如此）。

 

3.B⁺-tree

B⁺-tree：是应文件系统所需而产生的一种B-tree的变形树。

一棵m阶的B+树和m阶的B树的异同点在于：

1.有n棵子树的结点中含有n-1 个关键字； (此处颇有争议，B+树到底是与B 树n棵子树有n-1个关键字 保持一致，还是不一致：B树n棵子树的结点中含有n个关键字，待后续查证。暂先提供两个参考链接：①wikipedia http://en.wikipedia.org/wiki/B%2B_tree#Overview；②http://hedengcheng.com/?p=525。)

2.所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)

3.所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。 (而B 树的非终节点也包含需要查找的有效信息)