01-时间复杂度、对数器（python）、冒泡、选择、递归实质、归并、小和问题、逆序对、mid
1、时间复杂度
常数时间的操作：一个操作如果和数据量没有关系，每次都是
固定时间内完成的操作，叫做常数操作。
时间复杂度为一个算法流程中，常数操作数量的指标。常用O
（读作big O）来表示。
具体来说，在常数操作数量的表达式中，
只要高阶项，不要低阶项，也不要高阶项的系数，剩下的部分
如果记为f(N)，那么时间复杂度为O(f(N))。
评价一个算法流程的好坏，先看时间复杂度的指标，然后再分
析不同数据样本下的实际运行时间，也就是常数项时间。
例子一：理解时间复杂度
2、冒泡排序
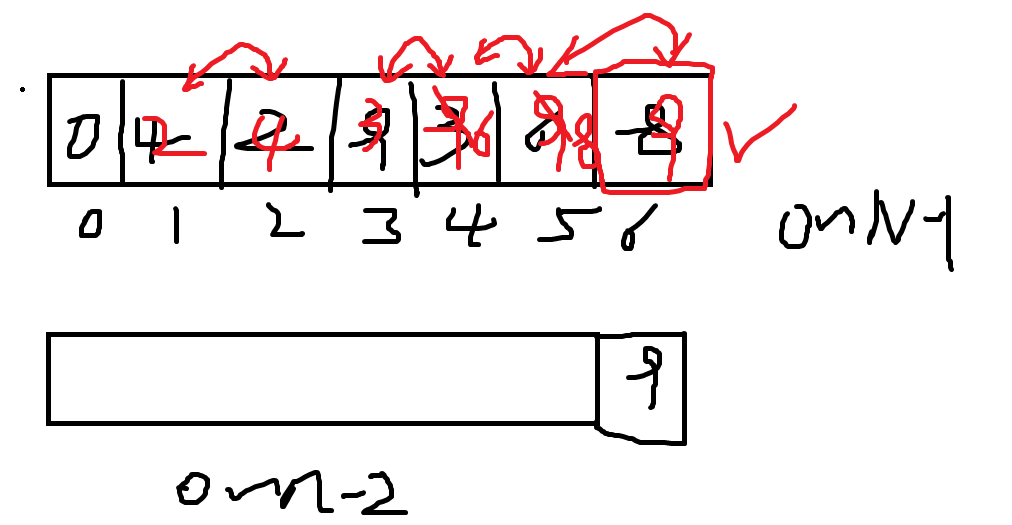
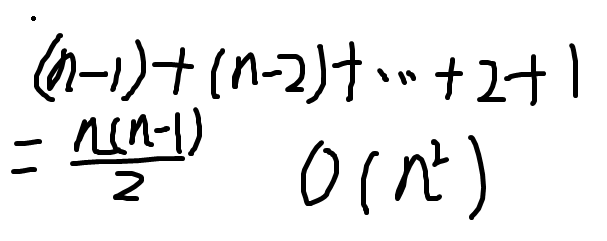
java版本
package basic_class_01;
import java.util.Arrays;
public class Code_00_BubbleSort {
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int e = arr.length - 1; e > 0; e--) {
for (int i = 0; i < e; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);
}
}
}
}
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
python版本
# 冒泡排序
# 时间复杂度O(N^2)
# 空间复杂度O(1) def bubble_sort(li):
if li is None and len(li) < 2:
return
for end in range(len(li) - 1, -1, -1):
for i in range(end):
if li[i] > li[i + 1]:
swap(li, i, i + 1)
return li # 优化版本
def bubble_sort1(li):
if li is None and len(li) < 2:
return
for end in range(len(li) - 1, -1, -1):
exchange = False # 设置哨兵
for i in range(end):
if li[i] > li[i + 1]:
swap(li, i, i + 1)
exchange = True
if not exchange:
return li
return li def swap(data, i, j):
temp = data[i]
data[i] = data[j]
data[j] = temp # for test
ret = bubble_sort([9, 2, 7, 8, 3, 2, 1])
print(ret)
3、选择排序
选择排序的细节讲解与复杂度分析
时间复杂度O(N^2)，额外空间复杂度O(1)
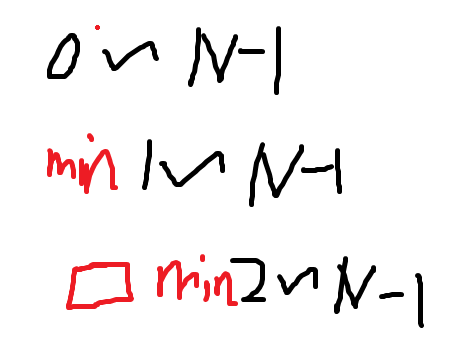
java版本
package basic_class_01;
import java.util.Arrays;
public class Code_02_SelectionSort {
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr, i, minIndex);
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
python版本
# 选择排序
# 时间复杂度O(N^2)
# 空间复杂度O(1) def selection_sort(li):
if li is None and len(li) < 2:
return
for i in range(len(li) - 1): # 当前n-1个确定好了，最后一个就确定ok
min_index = i
for j in range(i + 1, len(li)):
if li[j] < li[min_index]:
min_index = j
swap(li, i, min_index)
return li def swap(data, i, j):
data[i] = data[i] ^ data[j]
data[j] = data[i] ^ data[j]
data[i] = data[i] ^ data[j] # for test
ret = selection_sort([9, 2, 7, 8, 3, 2, 1])
print(ret)
4、插入排序
插入排序的细节讲解与复杂度分析
时间复杂度O(N^2)，额外空间复杂度O(1)
java版本
public static void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 1; i < arr.length; i++) {
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
python版本
# 插入排序
# 时间复杂度O(N^2)
# 空间复杂度O(1) def selection_sort(li):
if li is None and len(li) < 2:
return
for i in range(1, len(li)):
temp = li[i]
j = i - 1
while j >= 0 and temp < li[j]:
li[j + 1] = li[j] # 元素往后推一个位置
j -= 1
li[j + 1] = temp # 最小元素放在第一个位置
return li # for test
ret = selection_sort([9, 2, 7, 8, 3, 2, 1])
print(ret)
5、对数器
1、用途：验证算法是否正确的一种方式
3、实现
1.随机数组发生器
2.准备一个绝对正确的方法
3.大样本测试 500 000
java版本
package basic_class_01;
import java.util.Arrays;
public class Code_00_BubbleSort {
// 需要验证的算法？？
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int e = arr.length - 1; e > 0; e--) {
for (int i = 0; i < e; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);
}
}
}
}
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
// 1.随机数组发生器
// for test
public static int[] generateRandomArray(int maxSize, int maxValue) {
// Math.random() -> double [0,1)
// (int) ((size+1)*Math.random()) -> [0,size] 整数
// size = 6, size+1 = 7
// Math.random() -> [0,1) * 7 -> [0,7) double
// double -> int[0,6) -> int
// 生成长度随机的数组
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
}
return arr;
}
// 2.准备一个绝对正确的方法
// for test
public static void comparator(int[] arr) {
Arrays.sort(arr);
}
// 3.大样本测试 500 000
// for test
public static void main(String[] args) {
int testTime = 500000;
int maxSize = 100;
int maxValue = 100;
boolean succeed = true;
for (int i = 0; i < testTime; i++) {
int[] arr1 = generateRandomArray(maxSize, maxValue);
int[] arr2 = copyArray(arr1);
bubbleSort(arr1);
comparator(arr2);
if (!isEqual(arr1, arr2)) {
succeed = false;
break;
}
}
System.out.println(succeed ? "Nice!" : "Fucking fucked!");
int[] arr = generateRandomArray(maxSize, maxValue);
printArray(arr);
bubbleSort(arr);
printArray(arr);
}
//3.1 copy
// for test
public static int[] copyArray(int[] arr) {
if (arr == null) {
return null;
}
int[] res = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
res[i] = arr[i];
}
return res;
}
// 3.2 验证isEqual，长度一样，每位的数字一样
// for test
public static boolean isEqual(int[] arr1, int[] arr2) {
if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
return false;
}
if (arr1 == null && arr2 == null) {
return true;
}
if (arr1.length != arr2.length) {
return false;
}
for (int i = 0; i < arr1.length; i++) {
if (arr1[i] != arr2[i]) {
return false;
}
}
return true;
}
// 3.3 打印结果
// for test
public static void printArray(int[] arr) {
if (arr == null) {
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
python版本
import random # 我的方法
def bubble_sort(li):
if li is None or len(li) < 2:
return li
for end in range(len(li) - 1, -1, -1):
for i in range(end):
if li[i] > li[i + 1]:
swap(li, i, i + 1)
return li # 交换两个数字，与
def swap(data, i, j):
data[i] = data[i] ^ data[j]
data[j] = data[i] ^ data[j]
data[i] = data[i] ^ data[j] '''for test'''
# 1.随机数组发生器
def generate_random_array(max_size,max_vaule):
arr = []
arr_len = int((max_size+1)*random.random()) # 长度随机，不能大于max_size
for i in range(arr_len):
arr.append(int((max_vaule + 1) * random.random()) - int(max_vaule * random.random())) # value随机
return arr # 2.准备一个绝对正确的方法
def comparator(arr):
return sorted(arr) # 3.大样本测试 500 000
def main():
test_time = 500
max_size = 100
max_value = 100
succeed = True
for i in range(test_time):
arr1 = generate_random_array(max_size,max_value)
arr2 = copy_array(arr1) arr1 = bubble_sort(arr1) # 我的方法
arr2 = comparator(arr2) # 系统绝对正确的方法 if not is_equal(arr1,arr2):
succeed = False
break print("Nice") if succeed else print("Fucking fucked") arr = generate_random_array(max_size,max_value)
print_array(arr)
bubble_sort(arr)
print_array(arr) # 3.1 copy
def copy_array(arr):
if arr is None:
return None
res = []
for i in range(len(arr)):
res.append(arr[i])
return res # 3.2 验证isEqual，长度一样，每位的数字一样
def is_equal(arr1,arr2):
if (arr1 is None and arr2 is not None) or (arr1 is not None and arr2 is None):
return False
if arr1 is None and arr2 is None:
return True
if len(arr1) != len(arr2):
return False
for i in range(len(arr1)):
if arr1[i] != arr2[i]:
return False
return True # 3.3 打印结果
def print_array(arr):
if arr is None:
return
for i in range(len(arr)):
print(arr[i],end=' ')
print('\n') if __name__ == '__main__':
main()
6、递归
6.1 递归实质
剖析递归行为和递归行为时间复杂度的估算
一个递归行为的例子
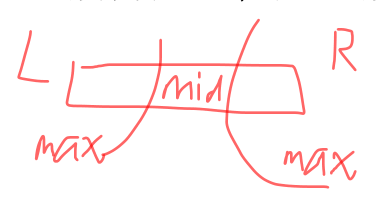
def get_max(arr,left,right):
if left == right:
return arr[left]
mid = (left+right)//2
max_left = get_max(arr,left,mid)
max_right = get_max(arr,mid+1,right)
return max(max_left,max_right) li = [4,3,2,1]
ret = get_max(li,0,len(li)-1)
print(ret) #
还原现场 ，系统栈
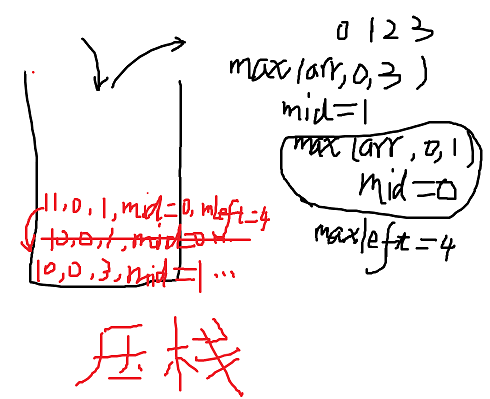
6.2 递归行为复杂度通式
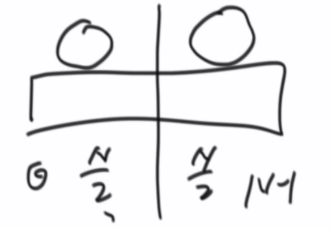
master公式的使用
T(N) = a*T(N/b) + O(N^d)
1) log(b,a) > d -> 复杂度为O(N^log(b,a))
2) log(b,a) = d -> 复杂度为O(N^d * logN)
3) log(b,a) < d -> 复杂度为O(N^d)
补充阅读：www.gocalf.com/blog/algorithm-complexity-and-master-
theorem.html
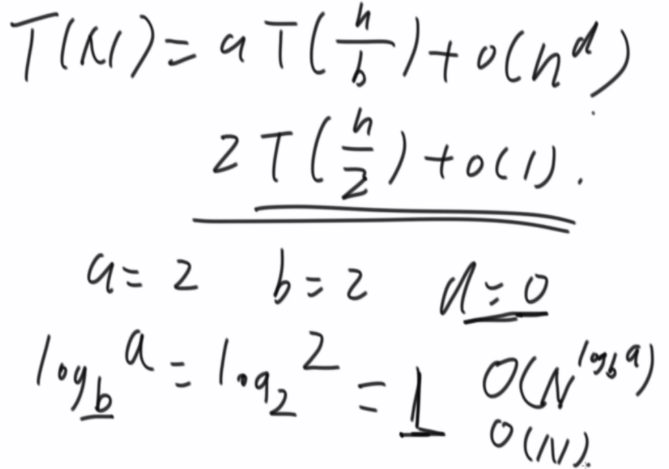
7、归并排序（递归、分治）
归并排序的细节讲解与复杂度分析
时间复杂度O(N*logN)，额外空间复杂度O(N)
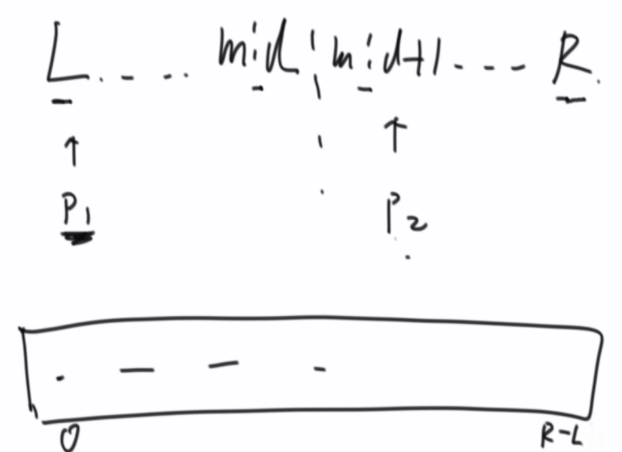
java版本
public static void mergeSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
mergeSort(arr, 0, arr.length - 1);
}
public static void mergeSort(int[] arr, int l, int r) {
if (l == r) {
return;
}
int mid = l + ((r - l) >> 1);
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
merge(arr, l, mid, r);
}
public static void merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[l + i] = help[i];
}
}
python版本
def mergeSort(arr):
if arr is None or len(arr) < 2:
return arr
merge_sort(arr,0,len(arr)-1)
return arr def merge_sort(arr,left,right):
if left == right:
return arr
mid = left + ((right-left)>>1) # left和right中点的位置 (L+R)//2
# 分解
merge_sort(arr,left,mid) # T(n/2)
merge_sort(arr,mid+1,right) # T(n/2) # 合并
merge(arr,left,mid,right) # O(n)
# T(n) = 2T(N/2)+ O(N) def merge(arr,left,mid,right):
temp = []
i,j = left,mid+1
while i<=mid and j <= right:
if arr[i]<arr[j]:
temp.append(arr[i])
i += 1
else:
temp.append(arr[j])
j +=1 # 两个必且有一个越界
while i<=mid:
temp.append(arr[i])
i += 1
while j<=right:
temp.append(arr[j])
j += 1 arr[left:right+1] = temp li = [3,1,2,4]
ret = mergeSort(li)
print(ret)
时间复杂度估算
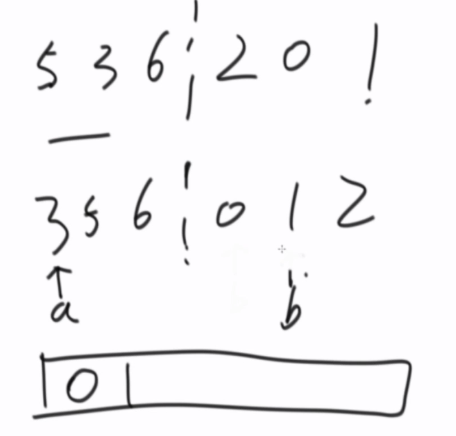
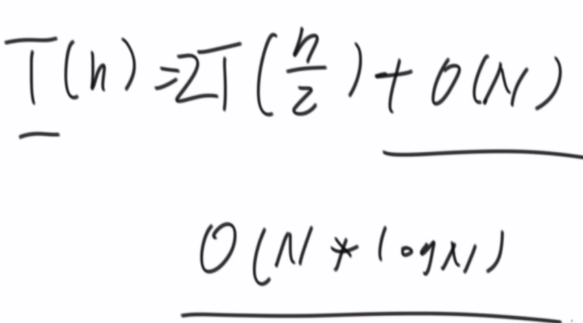
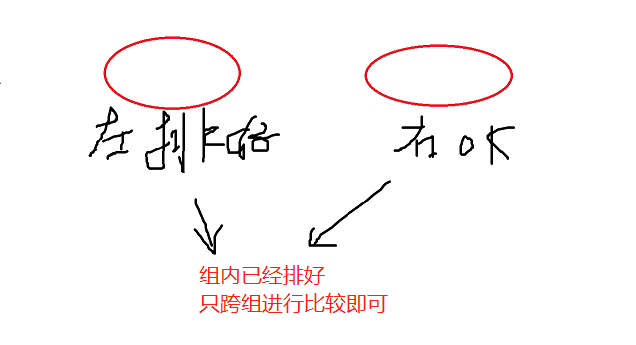
为什么归并排序比较快
其他排序，有很多无效的比较，浪费比较
8、小和问题
小和问题
在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组
的小和。
例子：
[1,3,4,2,5]
1左边比1小的数，没有；
3左边比3小的数，1；
4左边比4小的数，1、3；
2左边比2小的数，1；
5左边比5小的数，1、3、4、2；
所以小和为1+1+3+1+1+3+4+2=16
4*1 + 2*3 + 1*4 + 1*2
java版本
public static int smallSum(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
return mergeSort(arr, 0, arr.length - 1);
}
public static int mergeSort(int[] arr, int l, int r) {
if (l == r) {
return 0;
}
int mid = l + ((r - l) >> 1);
return mergeSort(arr, l, mid) + mergeSort(arr, mid + 1, r) + merge(arr, l, mid, r);
}
public static int merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
int res = 0;
while (p1 <= m && p2 <= r) {
res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[l + i] = help[i];
}
return res;
}
python版本
def small_sum(arr):
if arr is None or len(arr) < 2:
return arr
return merge_sort(arr, 0, len(arr) - 1) def merge_sort(arr, l, r):
if l == r:
# return arr 要进行res相加操作
return 0 m = l + ((r - l) >> 1) # m = (L+R)//2
return merge_sort(arr, l, m) + merge_sort(arr, m + 1, r) + merge(arr, l, m, r) def merge(arr, l, m, r):
temp = []
i, j = l, m + 1 res = 0 # 每次merge产生的 小和 while i <= m and j <= r:
res += (r - j + 1) * arr[i] if arr[i] < arr[j] else 0 # 小和 if arr[i] < arr[j]:
temp.append(arr[i])
i += 1
else:
temp.append(arr[j])
j += 1 # 两个必且有一个越界
while i <= m:
temp.append(arr[i])
i += 1
while j <= r:
temp.append(arr[j])
j += 1 for i in range(len(temp)):
arr[l + i] = temp[i] return res arr = [1,3,4,2,5]
print(small_sum(arr))
res += (r - j + 1) * arr[i] if arr[i] < arr[j] else 0 # 小和
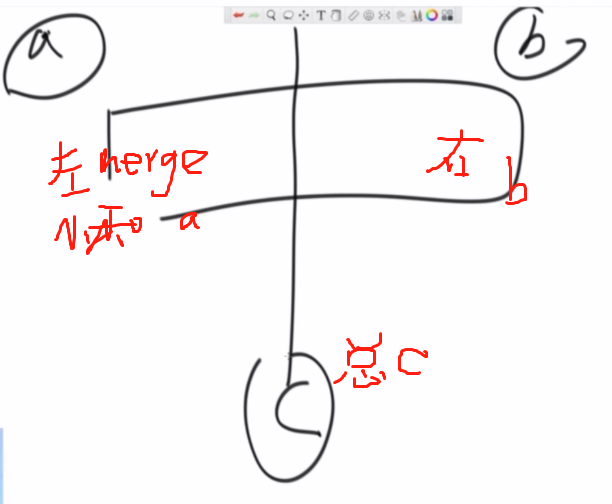
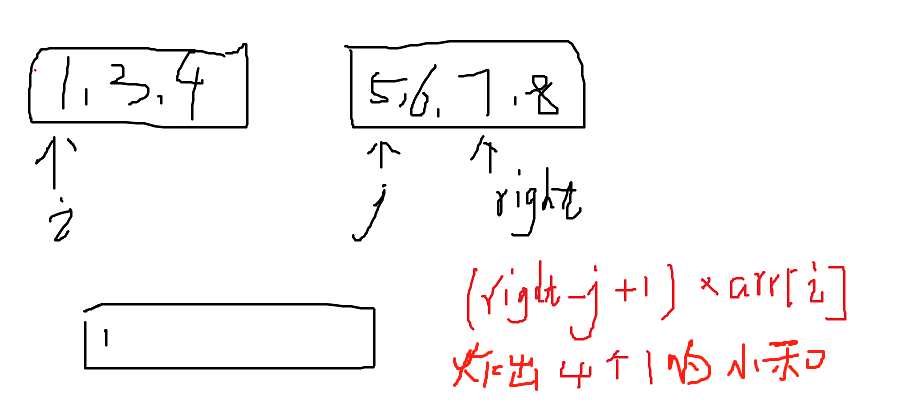
左神语录
有一个思路要给大家贯彻到底的
所有东西都是技术问题
你写不出来的原因是因为缺乏练习，
而不是你这个人笨
你知道吗，真的是要建立这种信心 因为我就是那样的阶段趟过来的，
这其中的辛苦确实都知道
9、逆序对问题
在一个数组中，左边的数如果比右边的数大，则折两个数构成一个逆序对，请打印所有逆序
对。
10、取mid的几种方法
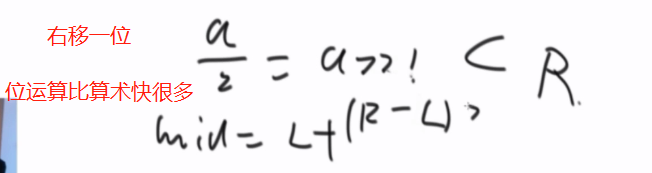
11、交换两个数的值
方法1：
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp; 方法2：
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
Z、总结
1、时间复杂度
big O 代表常数操作
只要高阶项，不要低阶项，也不要高阶项的系数
2、冒泡
时间复杂度O(N^2)
额外空间复杂度O(1)
3、选择
时间复杂度O(N^2)
额外空间复杂度O(1)
6、递归实质
还原现场：系统压栈操作
7、递归的master公式
T(N) = a*T(N/b) + O(N^d)
8、归并排序 （重要）
递归、分治 思想
时间复杂度O(N*logN)
额外空间复杂度O(N)
归并排序为什么比其他的快？
其他排序，有很多无效的比较，浪费比较
9、小和问题
例子：
[1,3,4,2,5]
1左边比1小的数，没有；
3左边比3小的数，1；
4左边比4小的数，1、3；
2左边比2小的数，1；
5左边比5小的数，1、3、4、2；
所以小和为1+1+3+1+1+3+4+2=16
4*1 + 2*3 + 1*4 + 1*2
归并合并的时候，每次炸出 小和
炸出 （right-j+1）* arr[i]
炸出 4个 1 的小和
炸出 2个 3 的小和
炸出 1个 4 的小和
炸出 1个 2 的小和
10、逆序对问题
在一个数组中，左边的数如果比右边的数大，
则折两个数构成一个逆序对，请打印所有逆序对
也用归并排序
11、取mid的几种方法
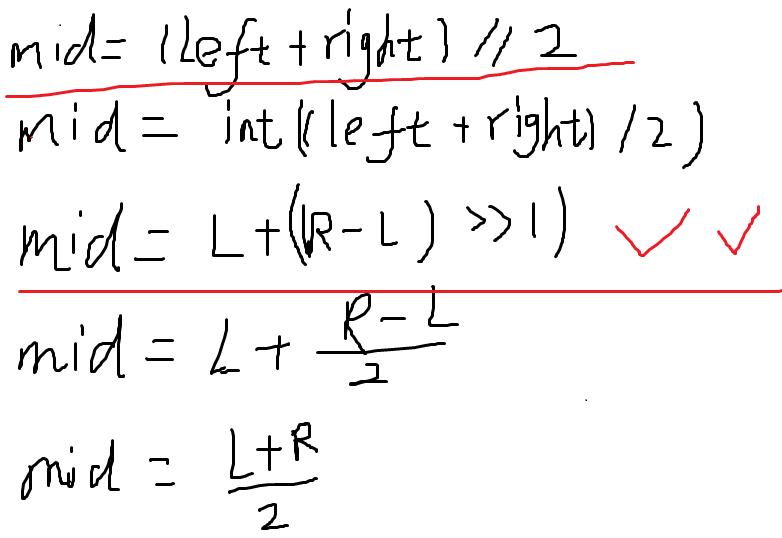
12、交换两个数的值
方法1：
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp; 方法2：
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
左神语录
有一个思路要给大家贯彻到底的
所有东西都是技术问题
你写不出来的原因是因为缺乏练习，
而不是你这个人笨
你知道吗，真的是要建立这种信心 因为我就是那样的阶段趟过来的，
这其中的辛苦确实都知道
准备模板，必要裸奔取考试
1、对数器
2、堆，排序
01-时间复杂度、对数器（python）、冒泡、选择、递归实质、归并、小和问题、逆序对、mid的更多相关文章
- 左神算法第一节课：复杂度、排序（冒泡、选择、插入、归并）、小和问题和逆序对问题、对数器和递归（Master公式）
第一节课 复杂度 排序(冒泡.选择.插入.归并) 小和问题和逆序对问题 对数器 递归 1. 复杂度 认识时间复杂度常数时间的操作:一个操作如果和数据量没有关系,每次都是固定时间内完成的操作,叫做常数 ...
- 算法初级面试题01——认识时间复杂度、对数器、 master公式计算时间复杂度、小和问题和逆序对问题
虽然以前学过,再次回顾还是有别样的收获~ 认识时间复杂度 常数时间的操作:一个操作如果和数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作. 时间复杂度为一个算法流程中,常数操作数量的指标.常 ...
- python 数据结构与算法之排序(冒泡,选择,插入)
目录 数据结构与算法之排序(冒泡,选择,插入) 为什么学习数据结构与算法: 数据结构与算法: 算法: 数据结构 冒泡排序法 选择排序法 插入排序法 数据结构与算法之排序(冒泡,选择,插入) 为什么学习 ...
- C++学习（三十八）（C语言部分）之 排序（冒泡 选择 插入 快排）
算法是解决一类问题的方法排序算法 根据元素大小关系排序 从小到大 从大到小冒泡 选择 插入 快排希尔排序 归并排序 堆排序 冒泡排序 从头到尾比较 每一轮将最大的数沉底 或者最小数字上浮 选择排序 1 ...
- JS实现对数器
对数器的概念和使用 对数器一般用于验证你写的算法是否正确,因为自己写的测试用例可能写的考虑不够全面. 0.有一个你想测试的方法a 1.实现一个绝对正确但是时间复杂度不好的方法b 2.实现一个随机样本产 ...
- 史上最详细的C语言和Python的选择排序算法
未经同意,请勿转载!如有收货,请留一赞,不胜感激! 同时欢迎加入我们的qq交流群:326079727 话不多说上代码: C语言: //选择排序走起 //原理:吃透原理再去实现,选择排序也是类似于冒泡排 ...
- python中的递归
python中的递归 关注公众号"轻松学编程"了解更多. 文章更改后地址:传送门 间接或直接调用自身的函数被称为递归函数. 间接: def func(): otherfunc() ...
- python 内置&&递归
lambda 优点: 1:可以简单使用一个脚本来替代我们的函数 2:不用考虑命名的问题 3:简化代码的可读性,不用跳转到def了,省去这样的步骤 内置函数:bif filter:过滤器 map:映射 ...
- Python 冒泡法排序
def sequence(disorder='', separators=''): arrays = disorder.split(separators) def desc(): for i in r ...
随机推荐
- C语言编程比赛WBS
- genymotion和adb的解决方法
问题: 安装了genymotion后.再单独安装了adb 然后在关闭genymotion后,输入adb devices,下方显示为空,然后打开genymotion,cmd输入adb devices,显 ...
- python之装饰器函数
本章内容 引入 装饰器的形成过程 开放封闭原则 谈装饰器主要功能和装饰器固定结构 带参数的装饰器 多个装饰器装饰一个函数 引入 作为一个会写函数的python开发,我们从今天开始要去公司上班了.写了一 ...
- [Linux.NET]在CentOS 7.x中编译方式安装Nginx
Nginx是一款轻量级的Web 服务器/反向代理服务器及电子邮件(IMAP/POP3)代理服务器,并在一个BSD-like 协议下发行.由俄罗斯的程序设计师Igor Sysoev所开发,供俄罗斯大型的 ...
- etcd raft如何实现Linearizable Read
Linearizable Read通俗来讲,就是读请求需要读到最新的已经commit的数据,不会读到老数据. 对于使用raft协议来保证多副本强一致的系统中,读写请求都可以通过走一次raft协议来满足 ...
- AD域自定义属性《完整》
1.安装Active Directory 架构,下载:adminpak.msi安装. 2.以管理员运行cmd,执行:regsvr32 schmmgmt.dll(该命令将在计算机上注册“schmmgmt ...
- myeclipce项目导入eclipse中报错
1 找到新建页面所在的工程名字,然后左键选中,右键弹出功能菜单,选择Build Path,进入配置路径. 2 在java build path 页面的下选择Libraries栏目(默认选择),点击右侧 ...
- January 15th, 2018 Week 03rd Monday
We got things to do. Places to go. People to see. Futures to make. 我们有很多事情要做,有很多地方要去,有很多人要见,有很多美好的未来 ...
- 使用 React-Sketchapp 管理你的设计资产
首发:https://www.yuque.com/jingwhale/blog/do37mc 最近在整理设计规范的过程中,尝试使用了 Airbnb 公司发布的 react-sketchapp 工具.从 ...
- js从数组中删除指定值（不是指定位置）的元素
RT: js从数组中删除指定值的元素,注意是指定值,而不是指定位置. 比如数组{1,2,3,4,5},我要删除其中的元素3,但是这个3的位置我是不知道的,只知道要删除值为3的这一个元素,请问要怎么写? ...