对于一个n随机变量的联合分布，一般需要2**n-1个参数来表示这个分布。但是，我们可以通过随机变量之间的独立性，减少参数的个数。

naive Beyes model:

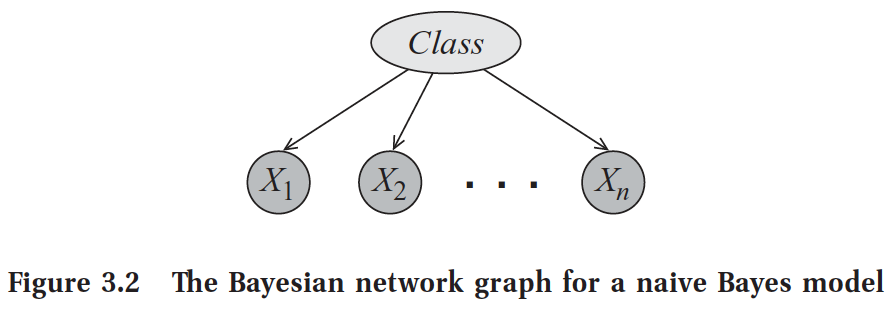
Bayesian Networks: 有向无环图（directed acyclic graph, DAG）

I-MAP:就是一个图G的独立性关系构成的集合是一个概率分布的独立性关系构成集合的子集。就是说这个图G在某种程度上可以等价于这个分布，但是这个图G上的边可能有冗余。

I-MAP to Factorization: 一个满足I-MAP的图G和P，那么这个P可以按照G上的local independence进行依赖分解。

Factorization to I-MAP: 如果P可以按照图G上的节点进行local independence分解，那么图G就是P的一个I-MAP

3.贝叶斯网络表示（The Bayesian Network Representation）的更多相关文章

  1. 基于MapReduce的贝叶斯网络算法研究参考文献

    原文链接(系列):http://blog.csdn.net/XuanZuoNuo/article/details/10472219 论文: 加速贝叶斯网络:Accelerating Bayesian ...

  2. 概率图模型（PGM） —— 贝叶斯网络（Bayesian Network）

    概率图模型是图论与概率方法的结合产物.Probabilistic graphical models are a joint probability distribution defined over ...

  3. PGM学习之六 从有向无环图（DAG）到贝叶斯网络（Bayesian Networks）

    本文的目的是记录一些在学习贝叶斯网络(Bayesian Networks)过程中遇到的基本问题.主要包括有向无环图(DAG),I-Maps,分解(Factorization),有向分割(d-Separ ...

  4. （ZT）算法杂货铺——分类算法之贝叶斯网络(Bayesian networks)

    https://www.cnblogs.com/leoo2sk/archive/2010/09/18/bayes-network.html 2.1.摘要 在上一篇文章中我们讨论了朴素贝叶斯分类.朴素贝 ...

  5. PGM：有向图模型：贝叶斯网络

    http://blog.csdn.net/pipisorry/article/details/52489270 为什么用贝叶斯网络 联合分布的显式表示 Note: n个变量的联合分布,每个x对应两个值 ...

  6. 贝叶斯深度学习（bayesian deep learning）

      本文简单介绍什么是贝叶斯深度学习(bayesian deep learning),贝叶斯深度学习如何用来预测,贝叶斯深度学习和深度学习有什么区别.对于贝叶斯深度学习如何训练,本文只能大致给个介绍. ...

  7. darktrace 亮点是使用的无监督学习（贝叶斯网络、聚类、递归贝叶斯估计）发现未知威胁——使用无人监督 机器学习反而允许系统发现罕见的和以前看不见的威胁，这些威胁本身并不依赖 不完善的训练数据集。 学习正常数据，发现异常！

    先说说他们的产品:企业免疫系统(基于异常发现来识别威胁) 可以看到是面向企业内部安全的! 优点整个网络拓扑的三维可视化企业威胁级别的实时全局概述智能地聚类异常泛频谱观测 - 高阶网络拓扑;特定群集,子 ...

  8. PGM学习之五 贝叶斯网络

    本文的主题是“贝叶斯网络”(Bayesian Network) 贝叶斯网络是一个典型的图模型,它对感兴趣变量(variables of interest)及变量之间的关系(relationships) ...

  9. 机器学习&数据挖掘笔记_18（PGM练习二：贝叶斯网络在遗传图谱在的应用）

    前言: 这是coursera课程:Probabilistic Graphical Models上的第二个实验,主要是用贝叶斯网络对基因遗传问题进行一些计算.具体实验内容可参考实验指导教材:bayes ...

  10. PRML读书会第八章 Graphical Models（贝叶斯网络，马尔科夫随机场）

    主讲人 网神 (新浪微博: @豆角茄子麻酱凉面) 网神(66707180) 18:52:10 今天的内容主要是: 1.贝叶斯网络和马尔科夫随机场的概念,联合概率分解,条件独立表示:2.图的概率推断in ...

随机推荐

  1. 【ACM】 1231 最大连续子序列

    [1231 最大连续子序列 ** Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) To ...

  2. tomcat端口被占用的问题

    在dos下,输入  netstat   -ano|findstr  8080  //说明:查看占用8080端口的进程 显示占用端口的进程 taskkill  /pid  6856  /f  //说明, ...

  3. docker 报错： Job for docker.service failed because the control process exited with error code. See "systemctl status docker.service" and "journalctl -xe" for details.

    centos 启动docker服务报错: Job for docker.service failed because the control process exited with error cod ...

  4. keras 的svm做分类

    SVC继承了父类BaseSVC SVC类主要方法: ★__init__() 主要参数: C: float参数 默认值为1.0 错误项的惩罚系数.C越大,即对分错样本的惩罚程度越大,因此在训练样本中准确 ...

  5. UltralEdit 替换回车换行符

    打开 Ue 工具,写下内容,如下图: 然后按 Ctrl + r,输入 ^p,点击按钮 “全部替换”, 如下图:

  6. ASP.NET WebApi服务接口如何防止重复请求实现HTTP幂等性

    一.背景描述与课程介绍 明人不说暗话,跟着阿笨一起玩WebApi.在我们平时开发项目中可能会出现下面这些情况; 1).由于用户误操作,多次点击网页表单提交按钮.由于网速等原因造成页面卡顿,用户重复刷新 ...

  7. 修复恢复"可疑"的SQLServer数据库

    今天机房突然断电,DB连不上了,提示 无法打开数据库'MyDB'.恢复操作已将该数据库标记为 SUSPECT. 原因是断电导致DB文件损坏 通过SQL Server Management Studio ...

  8. centos7上 docket无权限的问题

    2.4 centos7上 docket无权限的问题,解决方案: https://stackoverflow.com/questions/24288616/permission-denied-on-ac ...

  9. 时间序列分析 异常分析 stl

    https://blog.csdn.net/snowdroptulip/article/details/79125912 https://www.cnblogs.com/runner-ljt/p/52 ...

  10. 【开源】C#信息抽取系统【招募C#队友】

    FDDC2018金融算法挑战赛02-A股上市公司公告信息抽取 更新时间 2018年7月11日 By 带着兔子去旅行 信息抽取是NLP里的一个实用内容.该工具的目标是打造一个泛用的自动信息抽取工具.使得 ...