poj 2763(RMQ+BIT\树链剖分)

传送门:Problem 2763

https://www.cnblogs.com/violet-acmer/p/9686774.html

题意：

　　一对夫妇居住在xx村庄，小屋之间有双向可达的道路，不会出现环，即所构成的图是个树，从ai小屋到bi小屋需要花费wi时间，一开始，女主角在s小屋，有两个询问，

　　①0 u : 她又个孩子在u屋，需要妈妈接她回家，输出从s到u所需的最短时间。

　　②1 x val : 由于种种原因，第x条道路的行走时间由之前的w[x]变为了val。

题解：

　　(1)RMQ+BIT

　　　　因为树中连接两点的路径是唯一的，如果我们对顶点进行合理排列的话，能否像链状时那样，进行类似的处理呢？

　　　　考虑利用RMQ计算LCA时所用的，按DFS访问的顺序排列顶点序列。

　　　　这样，u和v之间的路径，就是在序列中u 和 v 之间的所有边减去往返重复的部分得到的结果。

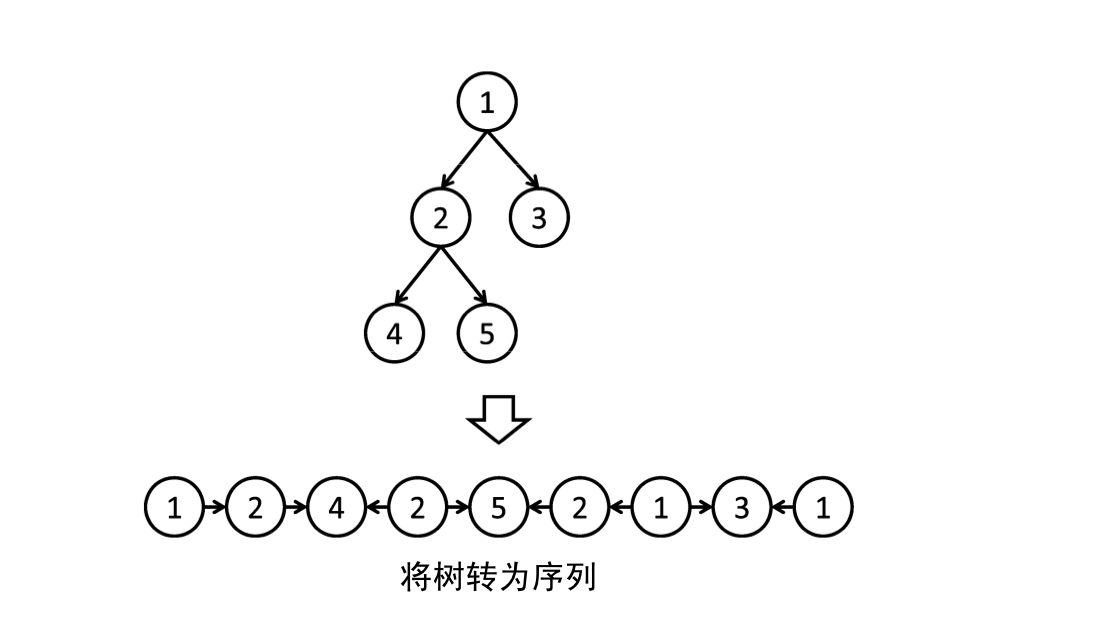
　　　　于是，只要令边的权重沿叶子方向为正，沿根方向为负，那么往返重复的部分就自然抵消了，于是有

　　　　　　　　(u,v之间的花费的时间)=(从LCA(u,v)到u的花费的时间和)+(从LCA(u,v)到v的花费的时间和);

　　　　同链状情况一样，利用BIT的话，计算权重和更新边权都可以在O(logn)时间内办到，而LCA也能够在O(longn)时间内求得。

　　(2)树链剖分

AC代码：

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<vector>
 using namespace std;
 #define pb push_back
 #define mem(a,b) (memset(a,b,sizeof a))
 #define lowbit(x) (x&(-x))
 ;

 int n,q,s;
 int w[maxn];//存储第 i 条边的权值
 struct Node
 {
     int to;
     int w;
     int id;
     Node(int to,int w,int id):to(to),w(w),id(id){}
 };
 vector<Node >G[maxn];
 void addEdge(int u,int v,int cost,int id)
 {
     G[u].pb(Node(v,cost,id));
     G[v].pb(Node(u,cost,id));
 }
 *maxn];//欧拉序列
 *maxn];//深度序列
 int id[maxn];//id[i] : 记录节点 i 在欧拉序列中第一次出现的位置
 *maxn];//边的下标，i*2 : 叶子方向 i*2+1 : 根方向
 int total;//记录欧拉序列的下标总个数，其实最终的 total = 2*n
 //================BIT==================
 *maxn];//树状数组
 void Add(int x,int val)
 {
     *maxn)
     {
         bit[x] += val;
         x += lowbit(x);
     }
 }
 int Sum(int x)
 {
     ;
     )
     {
         sum += bit[x];
         x -= lowbit(x);
     }
     return sum;
 }
 //=====================================
 //==================RMQ================
 struct RMQ
 {
     ][*maxn];
     void Init(){
         ;i < *maxn;++i)
             dp[][i]=i;
     }
     void ST()
     {
         );
         ;i <= k;++i)
             ;j <= (total-(<<i));++j)
                 ][j]] > depth[dp[i-][j+(<<(i-))]])//dp[i][j] : 记录的是下标
                     dp[i][j]=dp[i-][j+(<<(i-))];
                 else
                     dp[i][j]=dp[i-][j];
     }
     int Lca(int u,int v)
     {
         if(u > v)
             swap(u,v);
         )/log();
         <<k)+]])
             <<k)+]];
         return vs[dp[k][u]];//返回 u,v 的lca
     }
 }_rmq;
 //=====================================
 void Dfs(int u,int f,int d)
 {
     vs[total]=u;
     depth[total]=d;
     id[u]=total++;
     ;i < G[u].size();++i)
     {
         Node &e=G[u][i];
         if(e.to != f)
         {
             Add(total,e.w);//叶子方向，+e.w
             es[*e.id]=total;//记录朝向叶子方向的边
             Dfs(e.to,u,d+);
             vs[total]=u;
             depth[total++]=d;
             Add(total,-e.w);//根方向， -e.w
             es[*e.id+]=total;//记录朝向根方向的边
         }
     }
 }
 void Init()
 {
     _rmq.Init();
     total=;
     mem(bit,);
     ;i < maxn;++i)
         G[i].clear();
 }
 int main()
 {
     while(~scanf("%d%d%d",&n,&q,&s))
     {
         Init();
         ;i < n;++i)
         {
             int u,v;
             scanf("%d%d%d",&u,&v,w+i);
             addEdge(u,v,w[i],i);
         }
         Dfs(,-,);
         _rmq.ST();
         ;i <= q;++i)
         {
             int type;
             scanf("%d",&type);
             )
             {
                 int u;
                 scanf("%d",&u);
                 int lca=_rmq.Lca(id[u],id[s]);
                 printf(*Sum(id[lca]));
                 s=u;
             }
             else
             {
                 int x,val;
                 scanf("%d%d",&x,&val);
                 Add(es[x*],val-w[x]);//w[x] 变为 val,需要在原基础上加上 val-w[x]
                 Add(es[x*+],w[x]-val);//朝向根方向的加负值
                 w[x]=val;
             }
         }
     }
     ;
 }

RMQ+BIT