单源最短路径算法——Bellman-ford算法和Dijkstra算法

 BellMan-ford算法描述

1.初始化：将除源点外的所有顶点的最短距离估计值 dist[v] ← +∞, dist[s] ←0; 
2.迭代求解：反复对边集E中的每条边进行松弛操作，使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离；（运行|v|-1次） 
3.检验负权回路：判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点，则算法返回false，表明问题无解；否则算法返回true，并且从源点可达的顶点v的最短距离保存在 dist[v]中。

 BELLMAN-FORD(G, w, s)
 INITIALIZE-SINGLE-SOURCE(G,s)
 for i =1 to |G.V|-1　　// 实验证明最多只需|V|-1次外层循环，|V|-1次结束后，若图G中无负权回路，那么s到其他所有顶点的最短路径求得
 　　for each edge (u, v)∈E   　　//算法核心，松弛每一条边，维持三角不等式成立
 　　　　RELAX(u,v,w) //对每一条边进行松弛操作
 for each edge (u, v)∈E　　　　//进行完|V|-1次循环操作后，如果还能某条边还能进行松弛，说明到某个点的最短路径还未找到，那么必定是存在负权回路，返回FALSE
 　　if d[v] > d[u] + w(u, v)
 　　　　return FALSE
 return TRUE　　　　//若进行上面的松弛之后没有返回，说明所有的d值都不会再改变了，那么最短路径权值完全找到，返回TRUE

举例说明：

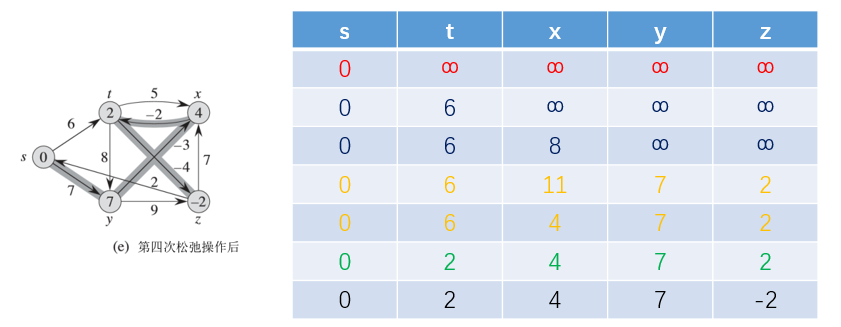
给定原点是s，初始化时候除了原点s之外，其他的都是无穷大的。因为有5个顶点，所以需要松弛的次数为5-1次

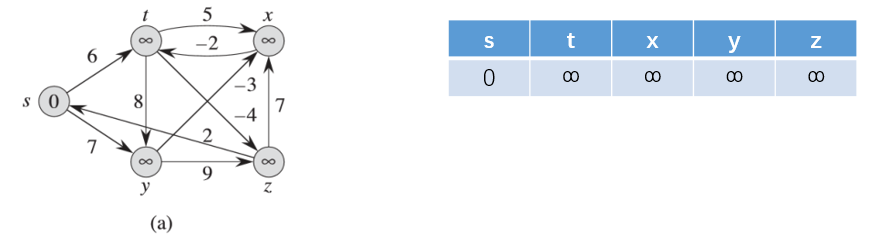
这里我们按照边<t,x>、<t,y>、<t,z>、<y,x>、<y,z>、<z,x>、<z,s>、<s,t>、<s,y>的顺序进行变得松弛操作。

第一次按照上述边进行松弛操作之后(实际上只对<s,t>、<s,y>进行操作)的结果为

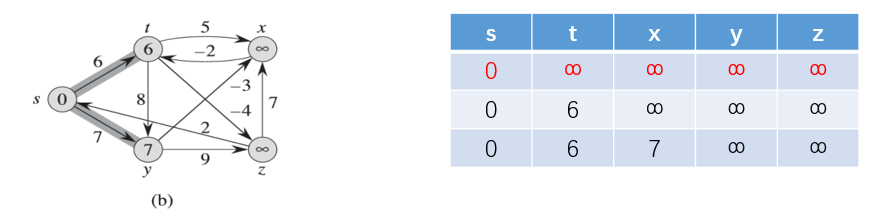
第二次按照给定边进行松弛操作之后：

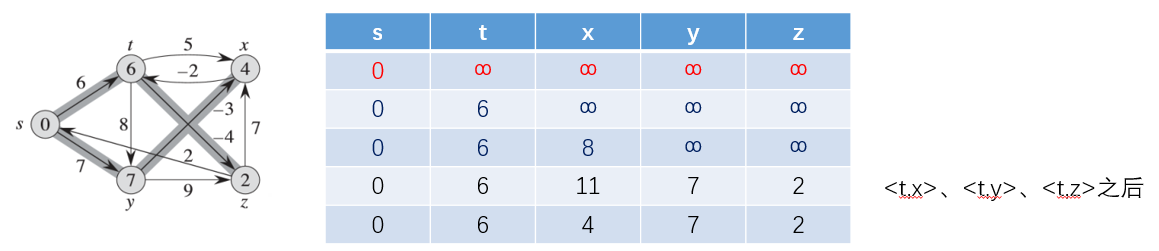
第三次松弛操作之后：

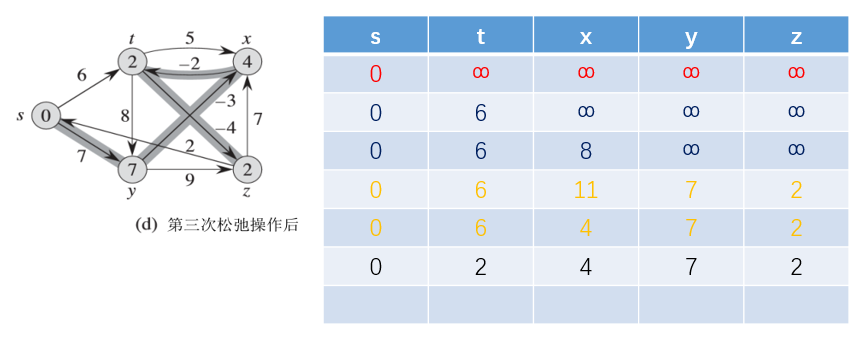
最后一次松弛操作：

给出实力代码

  #include <iostream>
  #include <cstdio>
  using namespace std;

  #define INF 0xffff      //权值上限
  #define maxe 5000       //边数上限
  #define maxn 100        //顶点数上限
  int n, m;       //顶点数、边数
  int d[maxn];    //保存最短路径权值的数组
 int parent[maxn];  //每个顶点的前驱顶点，用以还原最短路径树
 struct edge     //表述边的结构体，因为要对每一条边松弛
 {
     int u, v, w;    //u为边起点，v为边端点，w为边权值，可以为负
 }EG[maxe];

 bool Bellman_Ford(int s)    //计算从起点到所有顶点的
 {
     for(int i = ; i <= n; i++)     //初始化操作d[EG[j].v] > d[EG[j].u]+EG[j].w
     {
         d[i] = INF;
         parent[i] = -;
     }
     d[s] = ;
     bool flag;      //标记，判断d值是否更新，跳出外层循环的依据
     for(int i = ; i < n; i++)  //外层循环最多做n-1次
     {
         flag = false;   //初始为false,假设不需再更新
         for(int j = ; j < m; j++)  //对m条边进行松弛操作，若有更新，flag记为true
             if(d[EG[j].v] > d[EG[j].u]+EG[j].w)     //if d[v] > d[u] + w(u, v)，更新d[v]
             {
                 d[EG[j].v] = d[EG[j].u]+EG[j].w;
                 parent[EG[j].v] = EG[j].u;
                 flag = true;
             }
         if(!flag) break; //若松弛完每条边后，flag状态不变，说明未发现更新，可直接跳出循环
     }
     for(int i = ; i < m; i++)  //做完上述松弛后，如果还能松弛，说明存在负权回路，返回false
         if(d[EG[i].v] > d[EG[i].u]+EG[i].w)
             return false;
     return true;    //不存在负权回路，返回true
 }

 int main()
 {
     int st;
     printf("请输入n和m:\n");
     scanf("%d%d", &n, &m);
     printf("请输入m条边(u, v, w)：\n");
     for(int i = ; i < m; i++)
         scanf("%d%d%d", &EG[i].u, &EG[i].v, &EG[i].w);
     printf("请输入起点：");
     scanf("%d", &st);
     if(Bellman_Ford(st))
     {
         printf("不存在负权回路。\n");
         printf("源顶点到各顶点的最短路径权值为：\n");
         for(int i = ; i <= n; i++)
             printf("%d ", d[i]);
         printf("\n");
     }
 }

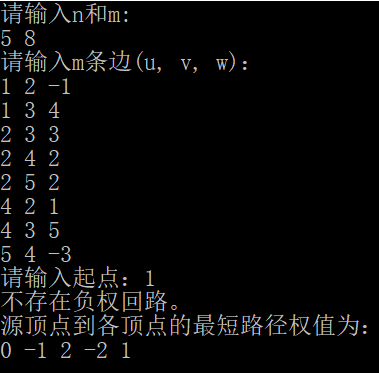
输入测试用例

1 2 -1
1 3 4
2 3 3
2 4 2
2 5 2
4 2 1
4 3 5
5 4 -3

​

Dijkstra算法

　(1)该算法要求所有边的权重均为非负值，即对于所有的边(u,v)∈E，ω(u,v)≥0，—— 既不能有负权重的边，更 不能 有负权重的环。算法在运行过程中维持的关键信息是一组结点集合S。从源结点s到该集合中每个节点之间的最短路径已经被找到。算法重复的从结点集合V-S中选择最短路径估计最小的结点u，将u加入到集合S中，然后对所有从u发出的边进行松弛操作。

　　(2)算法设计思想如下：

　　

　　(3)算法描述伪代码如下：

　　

　　(4)下面给出算法一些理解：

　　上述算法第一行执行的是d值和π值的初始化，第2行将集合S初始化为一个空集。算法所维持的循环不变式为Q=V-S，不变式在算法的while循环中保持不变。

　　第3行对最小优先队列进行初始化，将所有的结点V都放在队列里面。此时的S=∅。

　　在执行while循环的时候，从集合Q=V-S中抽取结点u，第6行将该结点加入到结合S里面，从而保持不变式成立。

　　然后将从u结点出发的所有结点进行松弛操作。如果一条经过结点u的路径能够使得从源结点s到结点v的最短路径权重比当前的估计值更小，就对v.d的数值和前驱结点进行更新操作。

　　(5)下面是一个实例

　　输入G，源结点1，结点集合V=<1,2,3,4,5,6>

　　①从源结点开始，此时集合S中只有结点1，从1出发的结点有6、2，所以更新此时的dist[2]和dist[6]的数值

　　 

　　②选择dist[2]和dist[6]中最小的值，即dist[6]=3,将结点6加入到集合S中，然后从更新结点6出发的结点2、5、4的路径值，分别更新为dist[2] = 5、dist[5] = 4、dist[4] = 9。

　　

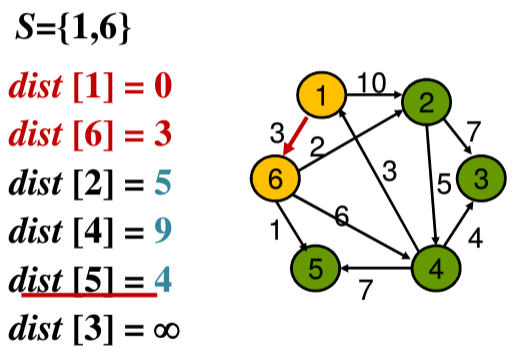
　　③选择dist[2] = 5、dist[5] = 4、dist[4] = 9中最小的值，即dist[5] = 4，将结点5加入到结合S中，然后更新从结点5出发的结点的值，由于没有从结点5出发的结点，所以直接进行下一步

　　

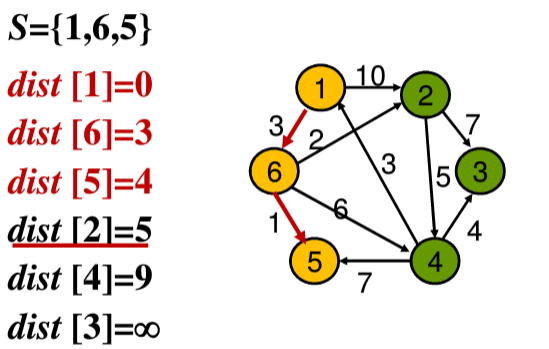
　　④第三步中选择dist[2] = 5，将结点2加入集合S中，然后更新从结点2出发的结点3、4的值，分别为dist[3] = 12、dist[4] = 9

　　

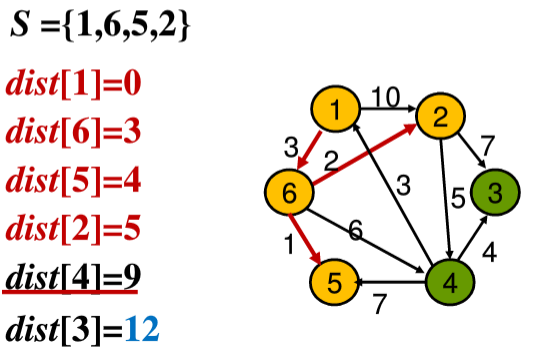
　　⑤从剩下的两个结点3、4中选择dist更小的结点4，将结点4加入集合S中，然后更新从结点4出发的结点3的值，判断之后，发现dist[3]依旧还是12

　　

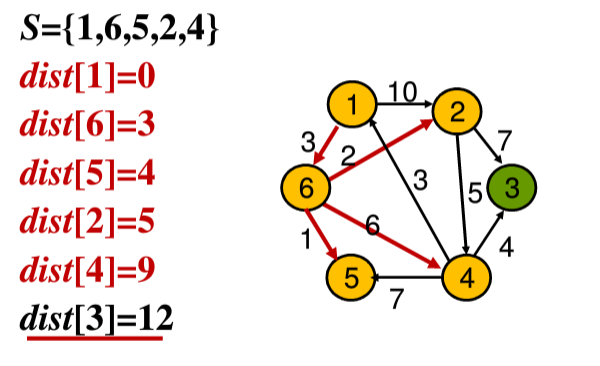
　　⑥最后一步，将结点3加入集合S中，此时以及更新完毕，找到了从结点1到达所有节点的最短路径