字符串匹配算法(三)-KMP算法

今天我们来聊一下字符串匹配算法里最著名的算法-KMP算法，KMP算法的全称是 Knuth Morris Pratt 算法，是根据三位作者（D.E.Knuth，J.H.Morris 和 V.R.Pratt）的名字来命名的。KMP算法和BM的算法思想类似，如果对BM算法不熟悉的同学可以看这篇文章BM算法详解。

KMP算法原理

KMP的算法核心思想是，当模式串b和主串a在进行匹配的时候，如果遇到不匹配的字符，我们希望找到一种规律，可以使得模式串b多向后滑动几位，跳过那些肯定不匹配的情况。

首先我们先明确二个定义：在模式串和主串匹配的过程中，我们把不能匹配的字符叫做坏字符，把已经匹配的那段字符叫做好前缀。在模式串和主串匹配的过程中，当遇到坏字符后，对于已经比对过的好前缀，能否找到一种规律，将模式串可以滑动多位呢。

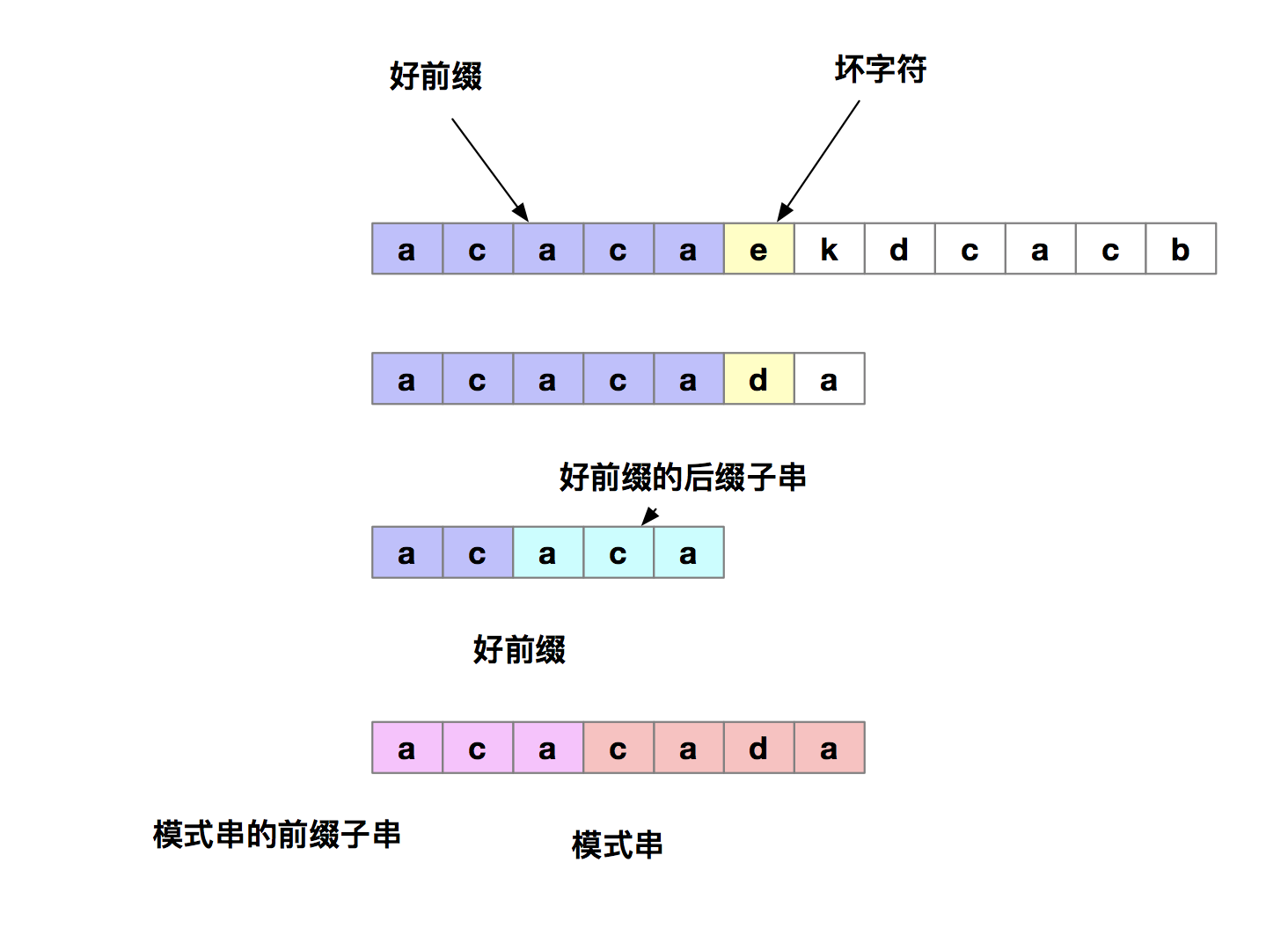
其实我们只需要拿好前缀本身，在他的后缀子串中，查找最长的那个可以跟好前缀的前缀子串匹配的。假设最长可匹配的那部分前缀子串是{u}，长度是k。我们可以把模式串一次性先后滑动j-k位，即当匹配到坏字符时，我们把j更新为k，然后i不变，然后再继续匹配。

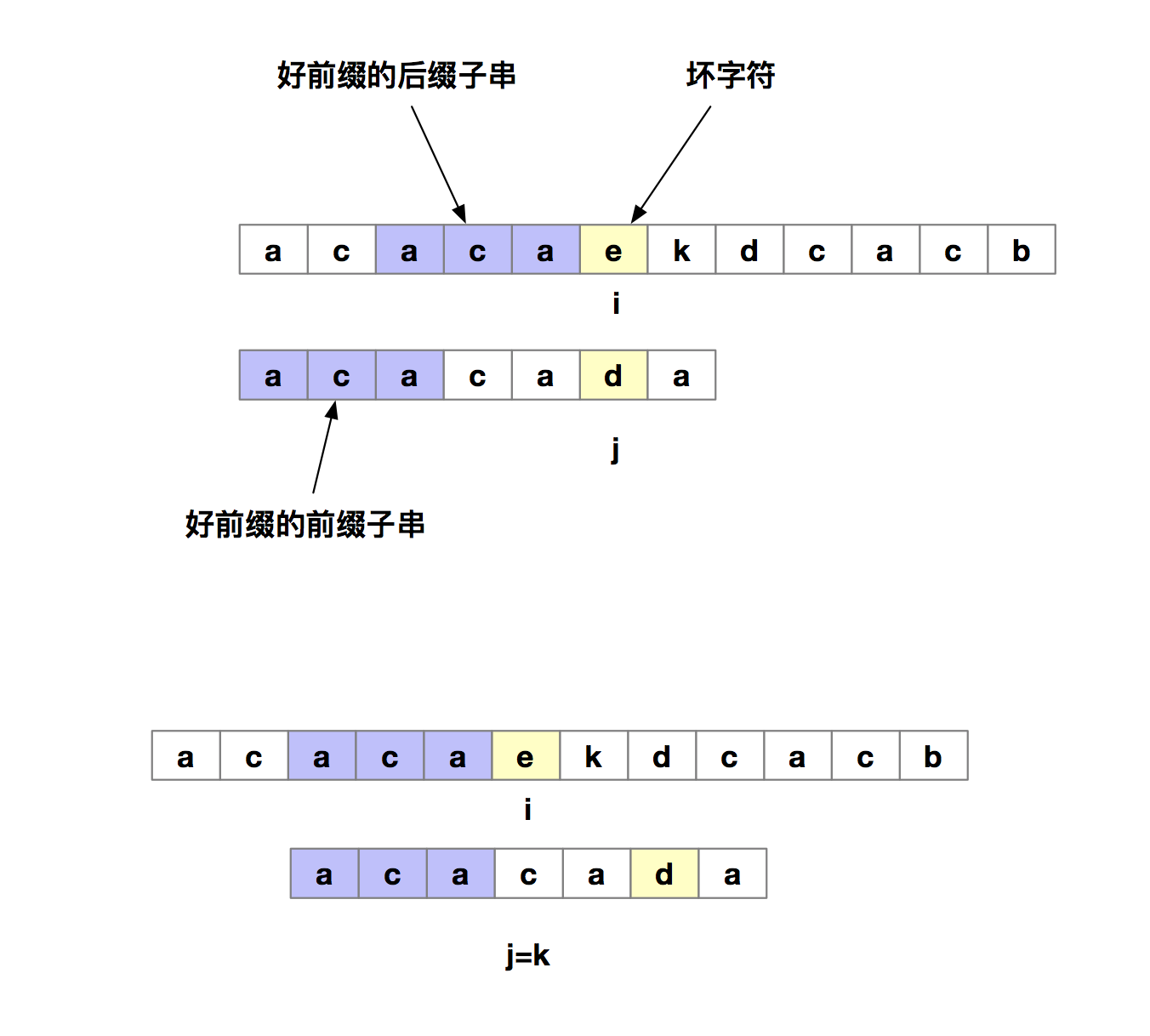
下面我们再明确两个定义，我们把好前缀的所有后缀子串中，最长的可以匹配前缀子串的那个后缀称为最长可匹配后缀子串，对应的前缀子串叫做最长可匹配前缀子串。那如何来求好前缀的最长可匹配前缀和后缀子串呢？

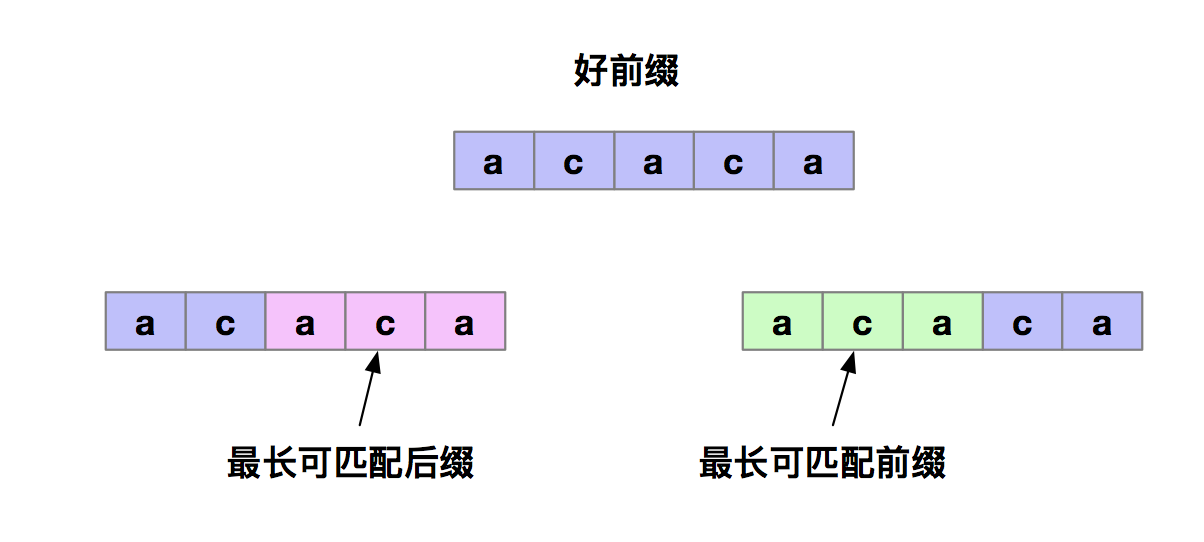
KMP算法是通过构建了一个数组来求的。该数组的下标是每个前缀结尾字符下标，该数组的值是这个前缀的最长可以匹配前缀子串的结尾字符下标。我们把这个数组定义为 next 数组，同时也可以称为是失效函数。如下图所示。

next数组的计算方法

我们来思考这么一个问题。如果next[i-1]=k-1，也就是说子串b[0, k-1]是b[0, i-1]的最长可匹配前缀子串。如果子串 b[0, k-1]的下一个字符 b[k]，与 b[0, i-1]的下一个字符 b[i]匹配，那么子串 b[0, k]就是 b[0, i]的最长可匹配前缀子串。所以，next[i]等于 k。如果 b[0, k-1]的下一字符 b[k]跟 b[0, i-1]的下一个字符 b[i]不相等呢？那我们这个时候就不能简单地通过 next[i-1]得到 next[i]了。这个时候该怎么办呢？我们假设 b[0, i]的最长可匹配后缀子串是 b[r, i]。如果我们把最后一个字符去掉，那 b[r, i-1]肯定是 b[0, i-1]的可匹配后缀子串，但不一定是最长可匹配后缀子串。所以，既然 b[0, i-1]最长可匹配后缀子串对应的模式串的前缀子串的下一个字符并不等于 b[i]，那么我们就可以考察 b[0, i-1]的次长可匹配后缀子串 b[x, i-1]对应的可匹配前缀子串 b[0, i-1-x]的下一个字符 b[i-x]是否等于 b[i]。如果等于，那 b[x, i]就是 b[0, i]的最长可匹配后缀子串。可是，如何求得 b[0, i-1]的次长可匹配后缀子串呢？次长可匹配后缀子串肯定被包含在最长可匹配后缀子串中，而最长可匹配后缀子串又对应最长可匹配前缀子串 b[0, y]。于是，查找 b[0, i-1]的次长可匹配后缀子串，这个问题就变成，查找 b[0, y]的最长匹配后缀子串的问题了。按照这个思路，我们可以考察完所有的 b[0, i-1]的可匹配后缀子串 b[y, i-1]，直到找到一个可匹配的后缀子串，它对应的前缀子串的下一个字符等于 b[i]，那这个 b[y, i]就是 b[0, i]的最长可匹配后缀子串。这块比较绕，可以先看代码，然后反过来多读几遍。

#b表示模式串
#m表示模式串的长度
def getNext(b,m):
     next=[-1]*m
     k=-1
     for i in range(1,m):
          while k!=-1 and b[k+1]!=b[i]:
               k=next[k]
          if b[k+1]==b[i]:
               k=k+1
​
          next[i]=k
     return next

　　

 我们有了next数组后，就可以动手来实现kmp算法了。

#b表示模式串
#m表示模式串的长度
def getNext(b,m):
     next=[-1]*m
     k=-1
     for i in range(1,m):
          while k!=-1 and b[k+1]!=b[i]:
               k=next[k]
          if b[k+1]==b[i]:
               k=k+1

          next[i]=k
     return next

def kmp(a,n,b,m):
     next=getNext(b,m)
     print(next)
     j=0
     for i in range(n):
          while j>0 and a[i]!=b[j]:
               j=next[j-1]+1

          if(a[i]==b[j]):
               j=j+1

          #找到匹配模式串的了
          if(j==m):
               return i-m+1

     return -1

到此为止，我们的kmp算法就学完了。更多硬核知识，请关注公众号。