如何鉴定全基因组加倍事件（WGD）

目前鉴定全基因组加倍（whole-genome duplication events）有3种

• 通过染色体共线性（synteny）

方法是比较两个基因组的序列，并将同源序列的位置绘制成点状图，如果能在点状图中发现比较明显的长片段，切较多，便可以推测是由于大尺度的基因组重复以后保留下来的痕迹，，而一般我们假想这种大尺度的基因组重复往往就是全基因组的重复。同样，对于单个物种而言，我们也可以绘制基因组内部的共线性的点状图，如果发现同一个物种的基因组的区间可以匹配到多个不同的区间中，这就暗示了该物种经历过基因组的加倍事件。利用共线性方法有一个弊端就是需要依赖全基因组的序列和基因顺序，因此只有做了全基因组测序才能进行共线性分析，不过这在基因组测序技术飞速发展的今天也不是什么难事。

在向日葵的这篇文章中，作者就用到了这种方法，三个点状图分别是向日葵、洋蓟、咖啡的基因组内部共线性分析。每个图的横纵坐标的方格代表一条染色体。例如，最左边的向日葵基因组有17条染色体。对角线当然是每个基因和自己本身的共线性。而对角线之外的点，代表分布在不同位置的旁系同源基因对。图中圆圈标注的位置，就是明显的基因组加倍事件的痕迹——3号染色体的一段和9号染色体的一段有明显的共线性。手机屏幕太小看不清？下面有高清图：

。

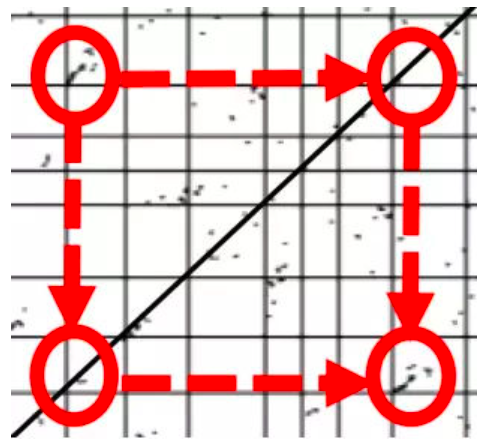
这个明显的痕迹就是向日葵独有的全基因组二倍化事件WGD-2留下的痕迹，当然其实还有很多，眼力好的同学可以自己连连看一下。那么前两次WGT留下的痕迹呢？全基因组加倍事件可以一次性增加一个物种所有的基因拷贝，在自然选择的作用下，倍增后的基因经历不同的命运：部分拷贝丢失，失去功能（假基因化）；部分拷贝获得新的功能（新功能化）；或者各自行使祖先基因的部分功能（亚功能化）

• 同义突变率ks

这是比较流行的方法。这种方法的背景是认为Ks值在某种程度上反映了同源基因的产生时间。而全基因组加倍事件会产生大量的同源基因，反映在Ks值上便是会有大量的Ks值接近的同源基因对的产生，这样通过绘制Ks值的分布图便可以发现明显的Ks值峰，而这些峰也就对应了全基因组加倍事件。这种方法是基于两点假设：1.基因的突变频率是稳定的；2.同义突变（Ks）不会影响物种适应性，因为并不会造成氨基酸序列的变化。

举个简单的例子，如果我们要进行人口调查，研究哪一年是生育高峰，我们不需要回去查医院的出生记录（或者根本没有），只需要调查现在的人口年龄构成，就可以看出哪个年龄是有一个高峰，那么那个年龄的人出生的年份，就是生育高峰。甚至，假如被调查的人都忘记了自己的年龄（一个很大的假如，可以认为是集体失忆造成的），我们都可以通过脸上的皱纹、头发的稀疏等外部特征来推断被调查人的年龄。如果是这样的话，我们同样是基于两点假设：1.皱纹的增长，头发的脱落是稳定的；2.皱纹和头发并不会影响死亡率。

言归正传，要进行Ks分析，首先要找到同源基因对，在不同的物种里面（比如向日葵-咖啡），是找最近的直系同源基因（ortholog），而在基因组内部（比如向日葵-向日葵），则是找最近的旁系同源基因（paralog）。通过计算这些基因的Ks值，我们就可以绘制出不同Ks值基因数量的分布图。

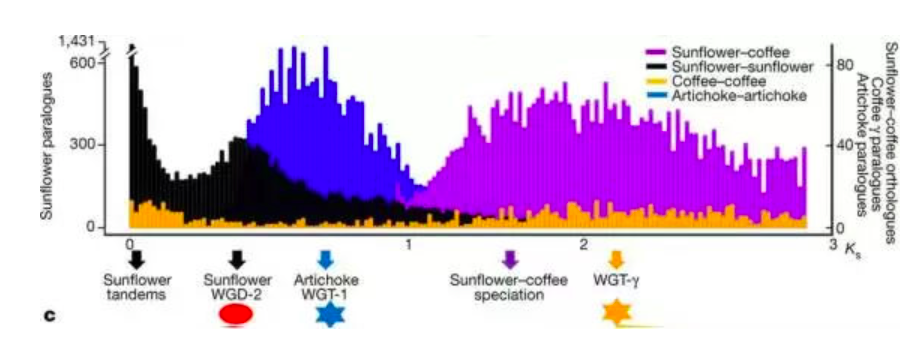
在这幅图中，横坐标是同源基因对的Ks值的分布（ 最大似然法F3x4 model），纵坐标为同源基因的数量，不同颜色的柱子代表不同的物种组合，比如黑色就是向日葵基因组内部的Ks分布。每一个峰都对应一次全基因组加倍事件，比如向日葵的WGD-2，因为发生的较晚，所以峰所在的位置Ks值较小，而且峰比较明显。而最下面橙色的峰，是咖啡发生的全基因组三倍化事件，峰值所在位置Ks值较大，但峰已经很不明显。同样，蓝色的峰为洋蓟的WGT-1事件，紫色的峰代表向日葵和咖啡的分化事件。最左边向日葵黑色的峰，其实是向日葵的重复序列造成的，不是真正的Ks峰。

不仅如此，有了Ks值，我们还可以计算全基因组加倍事件发生的时间，只要知道碱基同义替换的速率r就可以了。在这里，这篇文章的作者在一个神奇的网站www.timetree.org查询了物种的分化时间，向日葵和咖啡的分化时间是100MYA，那么根据公式：分化时间=Ks/2r，就可以计算每年每个同义替换位点发生替换的速率为r=8.25E-9。然后用这个r值去计算不同的基因组加倍事件发生的时间，最终得出了我们在上文提到的时间：WGTγ (Ks=2.02-2.71, 122-164 MYA)， WGT1 (Ks=0.63-0.82, 38-50 MYA) ，以及WGD2 (Ks=0.48, 29 MYA)。是不是跟做小学乘除法一样简单？

当然Ks值也有一些不可避免的限制，比如很难应用于比较古老的基因组加倍事件的识别，这是因为随着时间的推移，同源基因对之间的Ks值会发生变化，而对于古老的基因组加倍事件而言，其所产生的同源基因对的Ks值的变化可大可小，最后反映在Ks值的分布上就会发现方差很大的一些Ks，这样就很难推算是否有一个明显的Ks峰值了。另外，由于随着时间的延长，同义替换趋于饱和，会导致Ks值计算的偏差，对于寻找古老的基因组加倍事件造成困难。

• 系统发生组学的方法

系统发生组学是通过构建大量的基因树，然后比较基因树和物种关系的参考系统发生树，找到上面的差异，这些差异往往是由于基因重复导致的。如果能发现大量的基因树中在同一物种树节点上都有基因重复事件，那么一个比较直接的猜想就是这个节点发生了一次基因组的复制事件。系统发生组学的方法比较困难，计算量大，这里不再详述。

关注下方公众号可获得更多精彩

参考链接

1. 从人见人爱的向日葵说起——Ks与全基因组多倍化事件

2. The sunflower genome provides insights into oil metabolism, flowering and Asterid evolution