PBR(基于物理的渲染)学习笔记2
相关资料
https://www.cnblogs.com/dojo-lzz/p/13237686.html
理论
vec3 calculateFinalColor(PBRInfo pbrInputs, vec3 lightColor) {
// Calculate the shading terms for the microfacet specular shading model
vec3 F = specularReflection(pbrInputs);
float G = geometricOcclusion(pbrInputs);
float D = microfacetDistribution(pbrInputs);
// Calculation of analytical lighting contribution
vec3 diffuseContrib = (1.0 - F) * diffuse(pbrInputs);
vec3 specContrib = F * G * D / (4.0 * pbrInputs.NdotL * pbrInputs.NdotV);
// Obtain final intensity as reflectance (BRDF) scaled by the energy of the light (cosine law)
return pbrInputs.NdotL * lightColor * (diffuseContrib + specContrib);
}

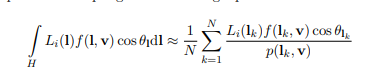

float3 SpecularIBL( float3 SpecularColor , float Roughness, float3 N, float3 V )
{
float3 SpecularLighting = 0;
const uint NumSamples = 1024; // 使用了1024个采样点
for( uint i = 0; i < NumSamples; i++ )
{
float2 Xi = Hammersley( i, NumSamples ); // 计算一个随机采样序列 float3 H = ImportanceSampleGGX( Xi, Roughness, N ); // 将一个二维采样序列转换成三维空间中的采样方向
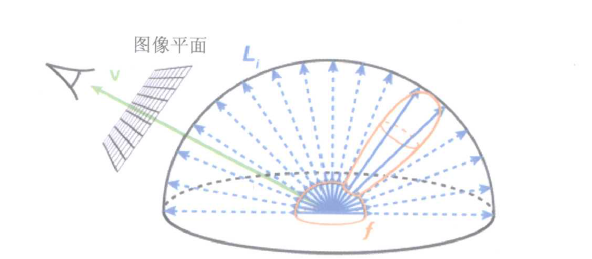
// 下面是计算法线、采样方向、视线等各种方向的一堆夹角
// 看上图L是从一个随机采样方向计算出得到的环境入射光源的反方向
float3 L = 2 * dot( V, H ) * H - V;
float NoV = saturate( dot( N, V ) );
float NoL = saturate( dot( N, L ) );
float NoH = saturate( dot( N, H ) );
float VoH = saturate( dot( V, H ) );
if( NoL > 0 )
{
// 计算环境光源颜色,envMap很可能是立方体贴图
float3 SampleColor = EnvMap.SampleLevel( EnvMapSampler , L, 0 ).rgb;
// 下面是计算BRDF的specular部分的G和F,这里并没有计算D,因为在BRDF/pdf过程中,D被消除掉了。
float G = G_Smith( Roughness, NoV, NoL );
float Fc = pow( 1 - VoH, 5 );
float3 F = (1 - Fc) * SpecularColor + Fc;
// Incident light = SampleColor * NoL
// Microfacet specular = D*G*F / (4*NoL*NoV)
// pdf = D * NoH / (4 * VoH)
// 上面pdf公式可以看出重要性跟粗糙度、法线与采样方向、视线与采样方向相关的。粗糙度是一个经过物理实验测量的值
SpecularLighting += SampleColor * F * G * VoH / (NoH * NoV);
}
}
return SpecularLighting / NumSamples; // 求和再取均值就是蒙特卡罗积分的体现
}
float3 ImportanceSampleGGX( float2 Xi, float Roughness, float3 N )
{
float a = Roughness * Roughness;
float Phi = 2 * PI * Xi.x; // 水平方向的phi
// theta不知道是怎么计算出来的,可能也是根据一个数学理论来计算的,这里可以看到有将粗糙度考虑进去
float CosTheta = sqrt( (1 - Xi.y) / ( 1 + (a*a - 1) * Xi.y ) );
float SinTheta = sqrt( 1 - CosTheta * CosTheta );
float3 H;
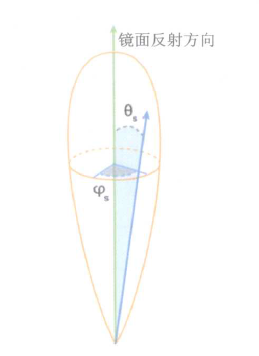
// 根据微分立体角坐标求得以该表面为原点,镜面反射方向为微分球的局部三维坐标系
H.x = SinTheta * cos( Phi );
H.y = SinTheta * sin( Phi );
H.z = CosTheta;
// 求表面切空间的的基底,切空间基底向量坐标系为世界坐标系
float3 UpVector = abs(N.z) < 0.999 ? float3(0,0,1) : float3(1,0,0);
float3 TangentX = normalize( cross( UpVector, N ) );
float3 TangentY = cross( N, TangentX );
// Tangent to world space
// 下面这个操作的前提是需要微分球的纵轴方向要与该点法向量的轴重合才行,而不是图片中说的镜面反射方向,这里可能是GPU GEM中文作者翻译错误了
// 因为微分球转换的三维坐标与且空间重合,所以这里是将微分三维坐标进行向量分解,最终得到一个三维空间坐标下的单位向量
return TangentX * H.x + TangentY * H.y + N * H.z;
}
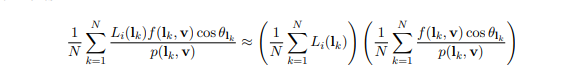
float3 PrefilterEnvMap( float Roughness, float3 R )
{
float3 N = R;
float3 V = R;
float3 PrefilteredColor = 0;
const uint NumSamples = 1024;
for( uint i = 0; i < NumSamples; i++ )
{
float2 Xi = Hammersley( i, NumSamples );
float3 H = ImportanceSampleGGX( Xi, Roughness, N );
float3 L = 2 * dot( V, H ) * H - V;
float NoL = saturate( dot( N, L ) );
if( NoL > 0 )
{
PrefilteredColor += EnvMap.SampleLevel( EnvMapSampler , L, 0 ).rgb * NoL;
TotalWeight += NoL;
}
}
return PrefilteredColor / TotalWeight;
}
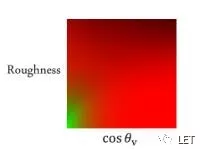
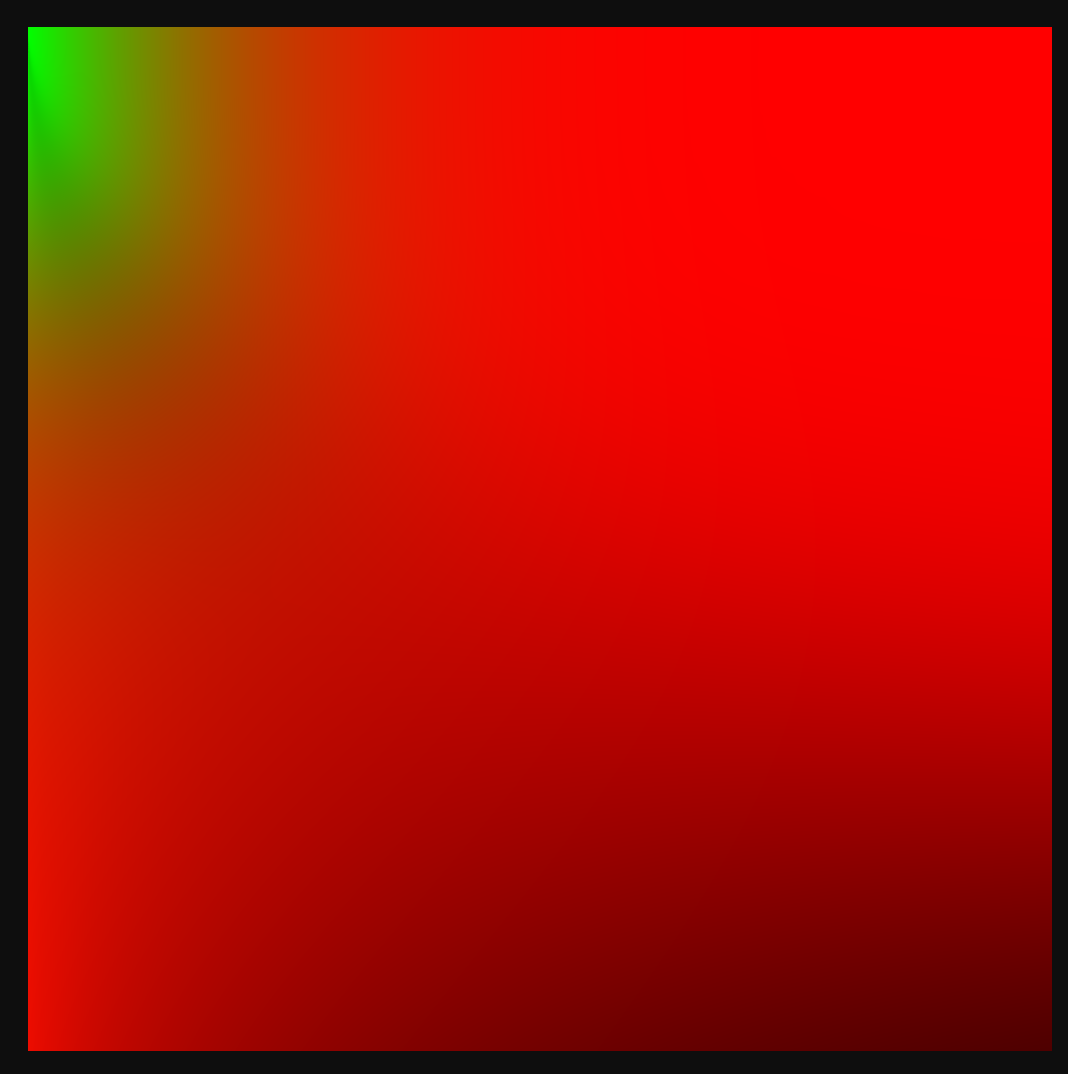
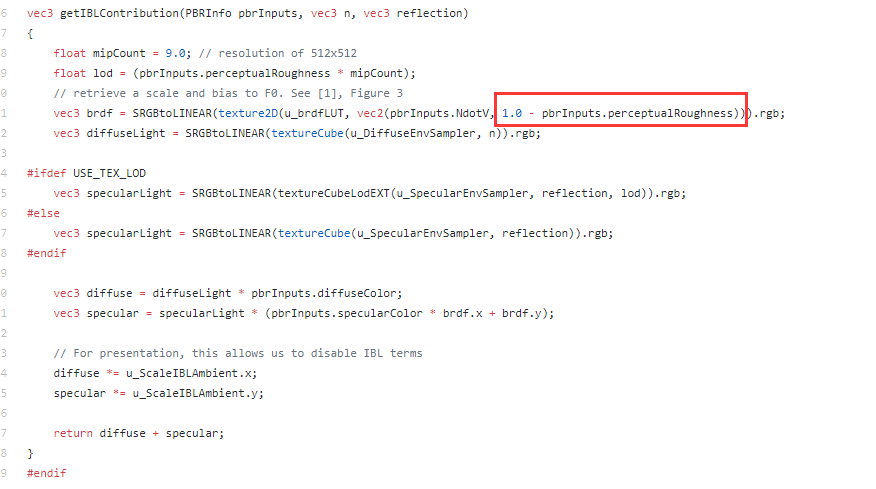
float2 IntegrateBRDF( float Roughness, float NoV )
{
float3 V;
V.x = sqrt( 1.0f - NoV * NoV ); // sin
V.y = 0;
V.z = NoV; // cos
float A = 0;
float B = 0;
const uint NumSamples = 1024;
for( uint i = 0; i < NumSamples; i++ )
{
float2 Xi = Hammersley( i, NumSamples );
float3 H = ImportanceSampleGGX( Xi, Roughness, N );
float3 L = 2 * dot( V, H ) * H - V;
float NoL = saturate( L.z );
float NoH = saturate( H.z );
float VoH = saturate( dot( V, H ) );
if( NoL > 0 )
{
float G = G_Smith( Roughness, NoV, NoL );
float G_Vis = G * VoH / (NoH * NoV);
float Fc = pow( 1 - VoH, 5 );
A += (1 - Fc) * G_Vis;
B += Fc * G_Vis;
}
}
return float2( A, B ) / NumSamples;
}
float3 ApproximateSpecularIBL( float3 SpecularColor , float Roughness, float3 N, float3 V )
{
float NoV = saturate( dot( N, V ) );
float3 R = 2 * dot( V, N ) * N - V;
float3 PrefilteredColor = PrefilterEnvMap( Roughness, R );
float2 EnvBRDF = IntegrateBRDF( Roughness, NoV );
return PrefilteredColor * ( SpecularColor * EnvBRDF.x + EnvBRDF.y );
}
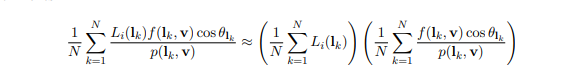


PBR(基于物理的渲染)学习笔记2的更多相关文章
- PBR(基于物理的渲染)学习笔记
PBR基本介绍 PBR代表基于物理的渲染,本质上还是 gl_FragColor = Emssive + Ambient + Diffuse + Specular 可能高级一些在考虑下AO也就是环境光遮 ...
- PBR:基于物理的渲染(Physically Based Rendering)+理论相关
一: 关于能量守恒 出射光线的能量永远不能超过入射光线的能量(发光面除外).如图示我们可以看到,随着粗糙度的上升镜面反射区域的会增加,但是镜面反射的亮度却会下降.如果不管反射轮廓的大小而让每个像素的镜 ...
- Canvas 数学、物理、动画学习笔记一
Canvas 第五章 数学.物理和运动学习笔记让人映像深刻的运动,需要我们不只是简单的知道如何移动对象,还需要知道怎么按用户期望看到的方式去移动它们.这些需要基于数学知识的基本算法和物理学作用.基于点 ...
- 基于物理的渲染——间接光照
在前面的文章中我们已经给出了基于物理的渲染方程: 并介绍了直接光照的实现.然而在自然界中,一个物体不会单独存在,光源会照射到其他的物体上,反射的光会有一部分反射到物体上.为了模拟这种环境光照的形式,我 ...
- 离屏渲染学习笔记 /iOS圆角性能问题
离屏渲染学习笔记 一.概念理解 OpenGL中,GPU屏幕渲染有以下两种方式: On-Screen Rendering 意为当前屏幕渲染,指的是GPU的渲染操作是在当前用于显示的屏幕缓冲区中进行. O ...
- MVC中使用Entity Framework 基于方法的查询学习笔记 (三)
紧接上文,我们已经学习了MVC数据上下文中两个常用的类,这两个类承载着利用函数方式进行数据查询的全部内容,我们既然已经了解了DbSet<TEntity> 是一个泛型集合,并且实现了一些接口 ...
- MVC中使用Entity Framework 基于方法的查询学习笔记 (一)
EF中基于方法的查询方式不同于LINQ和以往的ADO.NET,正因为如此,有必要深入学习一下啦.闲话不多说,现在开始一个MVC项目,在项目中临床学习. 创建MVC项目 1.“文件”--“新建项目”-- ...
- 基于PHP的AJAX学习笔记(教程)
本文转载自:http://www.softeng.cn/?p=107 这是本人在学习ajax过程所做的笔记,通过本笔记的学习,可以完成ajax的快速入门.本笔记前端分别使用原生态的javascript ...
- 基于python的接口测试学习笔记一(初出茅庐)
第一次写博客笔记,讲一下近来学习的接口自动化测试.网上查阅了相关资料,最后决定使用python语言写接口测试,使用的是python的第三方库requests.虽然python本身标准库中的 urlli ...
随机推荐
- Django之csrf中间件及auth模块使用
目录 一.基于配置文件的编程思想 1. importlib 模块 2. 配置文件 二.跨站请求伪造(csrf) 1.csrf简介以及由来 2.Django中的csrf中间件如何使用 2.1 普通for ...
- 创建AD域之后设置DNS服务访问外网
AD域内需要有DNS服务器,用于解析域内的计算机名,域内的计算解析公网的域名需要设置一个转发器(Forwarder). 一定要设置好自己的默认网关.DNS因为部署在AD服务器上,直接loopback地 ...
- Python 基础学习笔记(超详细版)
1.变量 python中变量很简单,不需要指定数据类型,直接使用等号定义就好.python变量里面存的是内存地址,也就是这个值存在内存里面的哪个地方,如果再把这个变量赋值给另一个变量,新的变量通过之前 ...
- JUC-ThreadLocalRandom
目录 Radndom类的局限性 ThreadLocalRandom 这个类是在JDK7中新增的随机数生成器,它弥补了Random类在多线程下的缺陷. Radndom类的局限性 在JDK7之前包括现在j ...
- MySQL:字段约束与索引
字段约束 MySQL的字段约束共四种: 约束名 关键字 描述 主键约束 PRIMARY KEY 字段值唯一,且不能为NULL 非空约束 NOT NULL 字段值不能为NULL 唯一约束 UNIQUE ...
- ACM STU week3
STU ACM训练week3(2.5-2.15) By@Xiezeju 训练计划的CP4配套资源库 训练时间安排 定期任务 任务 每日 进行1小时的盲打训练锻练手速 打字网站,最好注册账号以保存进度 ...
- MySQL 多表查询与事务的操作
表连接查询 什么是多表查询 # 数据准备 # 多表查询的作用 * 比如:我们想查询孙悟空的名字和他所在的部门的名字,则需要使用多表查询 # 如果一条 SQL 语句查询多张表,因为查询结果在多张不同的表 ...
- 用c++解一元二次方程
解方程 github项目地址 这两天得知初二的表妹学了一元二次方程,听说还不会解,我就想着试试用C语言编写解方程. 一元二次方程 用公式法 这种方法效果很好: #include"funct. ...
- JVM笔记 -- JVM的生命周期介绍
Github仓库地址:https://github.com/Damaer/JvmNote 文档地址:https://damaer.github.io/JvmNote/ JVM生命周期 启动 执行 退出 ...
- 【Azure API 管理】APIM CORS策略设置后,跨域请求成功和失败的Header对比实验
在文章"从微信小程序访问APIM出现200空响应的问题中发现CORS的属性[terminate-unmatched-request]功能"中分析了CORS返回空200的问题后,进一 ...
