ADAM : A METHOD FOR STOCHASTIC OPTIMIZATION

目录

• 概
• 主要内容
  • 算法
  • 选择合适的参数
  • 一些别的优化算法
  • AdaMax
  • 理论
• 代码

Kingma D P, Ba J. Adam: A Method for Stochastic Optimization[J]. arXiv: Learning, 2014.

@article{kingma2014adam:,

title={Adam: A Method for Stochastic Optimization},

author={Kingma, Diederik P and Ba, Jimmy},

journal={arXiv: Learning},

year={2014}}

概

鼎鼎大名.

主要内容

用\(f(\theta)\)表示目标函数, 随机最优通常需要最小化\(\mathbb{E}(f(\theta))\), 但是因为每一次我们都取的是一个小批次, 故实际上我们处理的是\(f_1(\theta),\ldots, f_T(\theta)\). 用\(g_t=\nabla_{\theta}f_t(\theta)\)表示第\(t\)步对应的梯度.

Adam 方法分别估计梯度\(\mathbb{E}(g_t)\)的一阶矩和二阶矩(Adam: adaptive moment estimation 名字的由来).

算法

注意: 下面的算法中关于向量的运算都是逐项(element-wise)的运算.

选择合适的参数

首先, 分析为什么会有

\[\tag{A.1}
\hat{m}_t \leftarrow m_t / (1-\beta_2^t), \\
\hat{v}_t \leftarrow v_t / (1-\beta_2^t).
\]

可以用归纳法证明

\[\tag{A.2}
m_t = (1-\beta_1) \sum_{i=1}^t \beta_1^{t-i} \cdot g_i \\
v_t = (1-\beta_2) \sum_{i=1}^t \beta_2^{t-i} \cdot g_i^2.
\]

倘若分布稳定: \(\mathbb{E}[g_t]=\mathbb{E}[g],\mathbb{E}[g_t^2]=\mathbb{E}[g^2]\), 则

\[\tag{A.3}
\mathbb{E}[m_t]=\mathbb{E}[g] \cdot(1-\beta_1^t) \\
\mathbb{E}[v_t]= \mathbb{E}[g^2] \cdot (1- \beta_2^t).
\]

这就是为什么会有(A.1)这一步.

Adam提出时的一个很大的应用场景就是dropout(正对梯度是稀疏的情况), 这是往往需要我们取较大的\(\beta_2\)(可理解为抵消随机因素).

既然\(\mathbb{E}[g]/\sqrt{\mathbb{E}[g^2]}\le 1\), 我们可以把步长\(\alpha\)理解为一个信赖域(既然\(|\Delta_t| \frac{<}{\approx} a\)).

另外一个很重要的性质是, 比如函数扩大(或缩小)\(c\)倍\(cf\), 此时梯度相应为\(cg\), 我们所对应的

\[\frac{c \cdot \hat{m}_t}{\sqrt{c^2 \cdot \hat{v}_t}}= \frac{\hat{m}_t}{\sqrt{\hat{v}_t}},
\]

并无变化.

一些别的优化算法

AdaGrad:

\[\theta_{t+1} = \theta_t -\alpha \cdot \frac{1}{\sqrt{\sum_{i=1}^tg_t^2}+\epsilon} g_t.
\]

RMSprop:

\[v_t = \beta_2 v_{t-1} + (1-\beta_2) g_t^2 \\
\theta_{t+1} = \theta_t -\alpha \cdot \frac{1}{\sqrt{v_t+\epsilon}}g_t.
\]

AdaDelta:

\[v_t = \beta_2 v_{t-1} + (1-\beta_2) g_t^2 \\
\theta_{t+1} = \theta_t -\alpha \cdot \frac{\sqrt{m_{t-1}+\epsilon}}{\sqrt{v_t+\epsilon}}g_t \\
m_t = \beta_1 m_{t-1}+(1-\beta_1)[\theta_{t+1}-\theta_t]^2.
\]

注: 均为逐项

AdaMax

本文还提出了另外一种算法

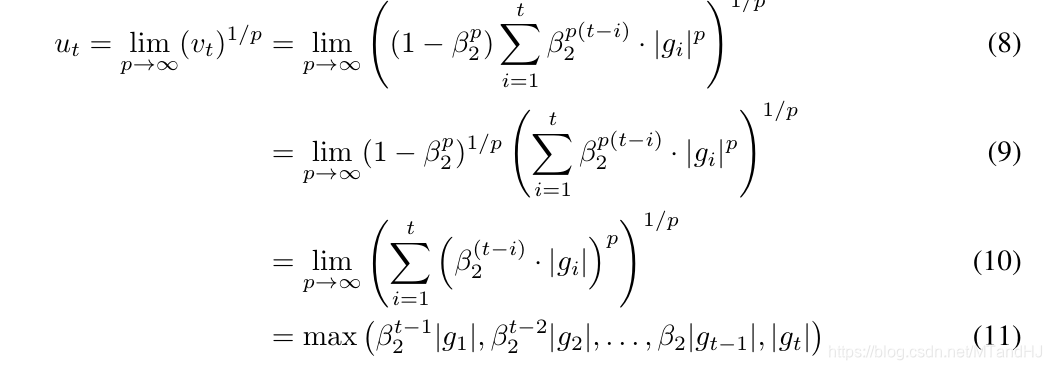
理论

不想谈了, 感觉证明有好多错误.

代码

import numpy as np

class Adam:

    def __init__(self, instance, alpha=0.001, beta1=0.9, beta2=0.999,
                 epsilon=1e-8, beta_decay=1., alpha_decay=False):
        """ the Adam using numpy
        :param instance: the theta in paper, should have the grad method to call the grads
                            and the zero_grad method for clearing the grads
        :param alpha: the same as the paper default:0.001
        :param beta1: the same as the paper default:0.9
        :param beta2: the same as the paper default:0.999
        :param epsilon: the same as the paper default:1e-8
        :param beta_decay:
        :param alpha_decay: default False, if True, we will set alpha = alpha / sqrt(t)
        """
        self.instance = instance
        self.alpha = alpha
        self.beta1 = beta1
        self.beta2 = beta2
        self.epsilon = epsilon
        self.beta_decay = beta_decay
        self.alpha_decay = alpha_decay
        self.initialize_paras()

    def initialize_paras(self):
        self.m = 0.
        self.v = 0.
        self.timestep = 0

    def update_paras(self):
        grads = self.instance.grad
        self.beta1 *= self.beta_decay
        self.beta2 *= self.beta_decay
        self.m = self.beta1 * self.m + (1 - self.beta1) * grads
        self.v = self.beta2 * self.v + (1 - self.beta2) * grads ** 2
        self.timestep += 1
        if self.alpha_decay:
            return self.alpha / np.sqrt(self.timestep)
        return self.alpha

    def zero_grad(self):
        self.instance.zero_grad()

    def step(self):
        alpha = self.update_paras()
        betat1 = 1 - self.beta1 ** self.timestep
        betat2 = 1 - self.beta2 ** self.timestep
        temp = alpha * np.sqrt(betat2) / betat1
        self.instance.parameters -= temp * self.m / (np.sqrt(self.v) + self.epsilon)

class PPP:

    def __init__(self, parameters, grad_func):
        self.parameters = parameters
        self.zero_grad()
        self.grad_func = grad_func

    def zero_grad(self):
        self.grad = np.zeros_like(self.parameters)

    def calc_grad(self):
        self.grad += self.grad_func(self.parameters)

def f(x):
    return x[0] ** 2 + 5 * x[1] ** 2

def grad(x):
    return np.array([2 * x[0], 100 * x[1]])

if __name__ == "__main__":

    x = np.array([10., 10.])
    x = PPP(x, grad)
    xs = []
    ys = []
    optim = Adam(x, alpha=0.4)
    for i in range(100):
        xs.append(x.parameters.copy())
        y = f(x.parameters)
        ys.append(y)
        optim.zero_grad()
        x.calc_grad()
        optim.step()
    xs = np.array(xs)
    ys = np.array(ys)
    import matplotlib.pyplot as plt
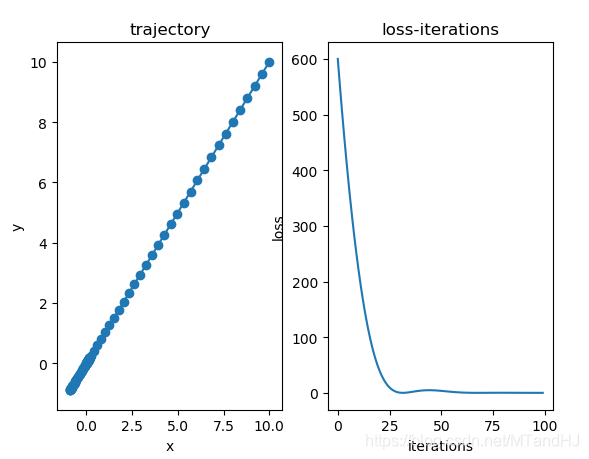
    fig, (ax0, ax1)= plt.subplots(1, 2)
    ax0.plot(xs[:, 0], xs[:, 1])
    ax0.scatter(xs[:, 0], xs[:, 1])
    ax0.set(title="trajectory", xlabel="x", ylabel="y")
    ax1.plot(np.arange(len(ys)), ys)
    ax1.set(title="loss-iterations", xlabel="iterations", ylabel="loss")
    plt.show()