M函数和M公式是Power Query专用的函数与公式，M代码是Power Query专用的用于实现查询功能的代码。M函数公式和M代码统称M语言。

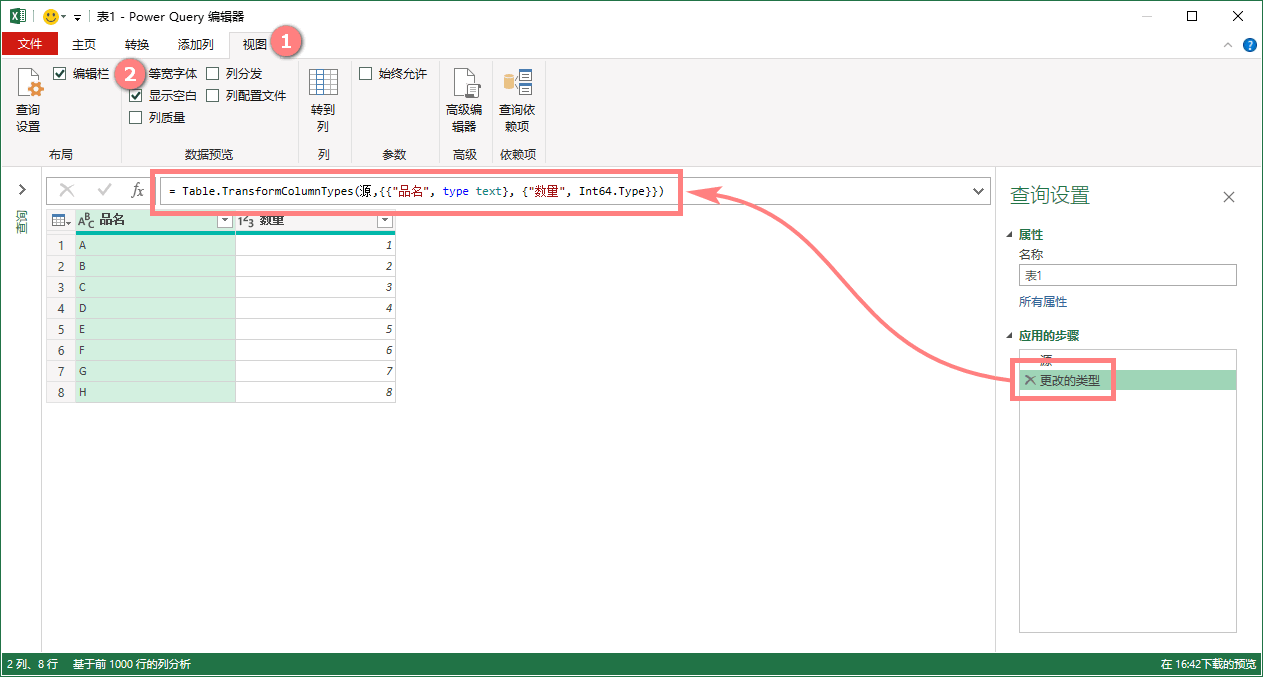
查看M公式：【编辑栏】

查看方法：在Power Query编辑器的【视图】选项卡下，勾选【编辑栏】，选取不同的【应用的步骤】即可看到【功能区】和【查询表】之间的M公式。

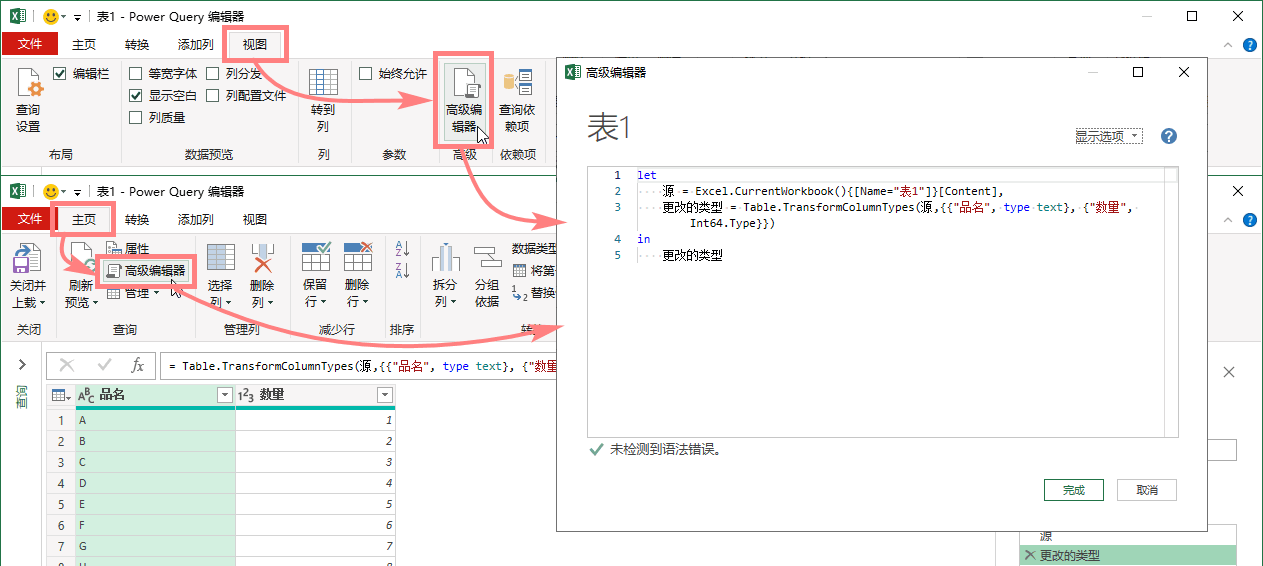
查看M代码：【高级编辑器】

查看方法：在Power Query编辑器的【视图】或者【主页】选项卡下，单击【高级编辑器】即可。

M语言的藏身之地（Power Query 之 M 语言）的更多相关文章

  1. M语言的写、改、删（Power Query 之 M 语言）

    M语言基本上和其他语言一样,用敲键盘的方式写入.修改.删除,这个是废话. M语言可以在[编辑栏]或[高级编辑器]里直接写入.修改.删除,这个也是废话. M语言还有个地方可以写入.修改.删除,就是[自定 ...

  2. Excel.CurrentWorkbook数据源（Power Query 之 M 语言）

    数据源: 任意超级表 目标: 将超级表中的数据加载到Power Query编辑器中 操作过程: 选取超级表中任意单元格(选取普通表时会自动增加插入超级表的步骤)>数据>来自表格/区域 M公 ...

  3. 自定义函数（Power Query 之 M 语言）

    数据源: 任意工作簿 目标: 使用自定义函数实现将数据源导入Power Query编辑器 操作过程: PowerQuery编辑器>主页>新建源>其他源>空查询 编辑栏内写入公式 ...

  4. 转换…Transform…（Power Query 之 M 语言）

    转换列: = Table.TransformColumns( 表, {{"列名1", 转换函数1, 数据类型1},-,{"列名n", 转换函数n, 数据类型n} ...

  5. 在【自定义列】中使用M函数（Power Query 之 M 语言）

    数据源: "品名"一列 目标: 提取品名中的首字符,生成新列:"品名简称" 解决方案: 在[自定义列]中使用M函数Text.Start 步骤: 打开[自定义列] ...

  6. M函数目录（Power Query 之 M 语言）

    2021-12-11更新 主页(选项卡) 管理列(组) 选择列 选择列Table.SelectColumns 删除列 删除列Table.RemoveColumns 删除其他列Table.SelectC ...

  7. Table.ReorderColumns移动…Reorder…（Power Query 之 M 语言）

    数据源: 至少两列 目标: 列顺序重新排列 操作过程: 选取待移动的列>鼠标拖放列标题 选取待移动的列>[转换]>[移动]>选取 M公式:  = Table.ReorderCo ...

  8. Table.FillDown填充Table.Fill…（Power Query 之 M 语言）

    数据源: 任意列中包含空单元格 目标: 将空单元格填充为其上或其下单元格中的内容 操作过程: 选取指定列>[转换]>[填充]>[向下] 选取指定列>[转换]>[填充]&g ...

  9. List.Sum…统计信息（Power Query 之 M 语言）

    数据源: 任意数据源,一列数值,一列非数值(文本) 目标: 对数值列进行求和等计算,对非数值列进行计数等计算 操作过程: 选取待计算的列>[转换]>[统计信息]>选取   M公式: ...

随机推荐

  1. 删除本地仓库中的lastUpdated文件.bat

    @echo off @ ECHO. @ ECHO. @ ECHO. 说 明 @ ECHO ------------------------------------------------------- ...

  2. 小白都能看懂的 Spring 源码揭秘之依赖注入(DI)源码分析

    目录 前言 依赖注入的入口方法 依赖注入流程分析 AbstractBeanFactory#getBean AbstractBeanFactory#doGetBean AbstractAutowireC ...

  3. 8.1 k8s使用PV/PVC做数据持久化运行redis服务，数据保存至NFS

    1.制作redis docker镜像 1.1 准备alpine基础镜像 # 下载 docker pull alpine:3.13 # 更改tag docker tag alpine:3.13 192. ...

  4. [NOI Online 2021 提高组] 积木小赛

    思路不说了. 想起来自己打比赛的时候,没睡好.随便写了个\(HASH\),模数开小一半分都没有. 然后学了\(SAM\),发现这个判重不就是个水题. \(SAM\)是字串tire的集合体. 随便\(d ...

  5. 51nod 1355 - 斐波那契的最小公倍数（Min-Max 容斥+莫比乌斯反演）

    vjudge 题面传送门 首先我们知道斐波那契数列的 lcm 是不太容易计算的,但是它们的 gcd 非常容易计算--\(\gcd(f_x,f_y)=f_{\gcd(x,y)}\),该性质已在我的这篇博 ...

  6. 33. Implement strStr()

    http://blog.csdn.net/justdoithai/article/details/51287649 理解与分析 Implement strStr() My Submissions Qu ...

  7. EXCEL excel中运用ctrl+D、ctrl+enter、ctrl+E批量填充数据

    在excel中,利用鼠标拖动可以快速向下或者向右填充序列或者复制单元格.但是利用快捷键也可以实现多种填充方式,本文就为大家介绍一些ctrl系列快捷键的填充,一起来看看吧. 封面tu 一,ctrl+D/ ...

  8. JAVA中null,"",equals,==相互之间使用详解

    "equals" 与 "==" "equals"只是比较值是否相同 而"=="则是比较两个变量是不是同一个变量,也应时是 ...

  9. JavaSE中级篇1 — 核心思想:面向对象 — 更新完毕

    1.面向对象编程思想(重点中的重点) 题外话: 其他都还可以是技术,但这里是走自己的路--面向对象编程,即:OOP,养成的思想就是:万物皆对象,懂得把东西抽离出来 这一部分记的理论知识很多,而且需要自 ...

  10. 19. 删除链表的倒数第 N 个结点

    目录 19.删除链表的倒数第N个节点 题目 题解-暴力 题解-哈希表 题解-双指针 19.删除链表的倒数第N个节点 题目 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点. 输入:he ...