opencv笔记---contours

一 Contour Finding

Contours使用 STL-style vector<> 表示，如 vector<cv::Point>, vector<cv::Point2f>。opencv中，使用函数 cv::findContours() 寻找contours， 具体函数定义如下：

void cv::findContours(cv::InputOutputArray image,

cv::OutputArrayofArrays contours,

cv::OutputArray hierarchy,

int mode,

int method,

cv::Point offset = cv::Point());

void cv::findContours(cv::InputOutputArray image,

cv::OutputArrayofArrays contours,

int mode,

int method,

cv::Point offset = cv::Point());

参数 image 为8位单通道输入图像，一般情况下，该图像可能由 cv::threshold(), cv::adaptiveThreshold 生成。当 image 由 cv::Canny() 生成时，cv::findContours() 仅当边缘图像为宽度为1的细区域图像，对于闭合边缘，可以使用内边缘或者外边缘代替边缘图像进行后续分析；但对于非闭合边缘，个人认为 cv::Canny() 生成的边缘图像不适合使用 cv::findContours() 进行查找；替代方案是使用边缘跟踪算法，将 cv::Canny()  生成边缘保存在 vector<cv::Point> 中，然后使用 Contours 相关分析进行更多分析。

参数 contours 为 vector<vector<cv::Point>>, vector<vector<cv::Point2f>>, 使用 array of arrays 结构可以同时保存多条 contours。

参数 hierarchy 为 vector<cv::Vec4i>, 每个元素对应一个 contour， 元素中4个整数表示该 contour 与其他 contour 之间的关系，具体关系如下：

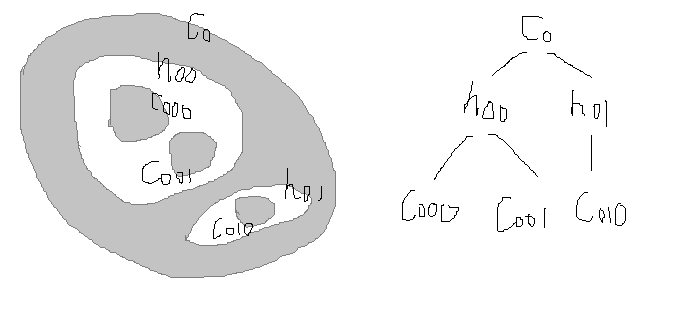
其中， c 表示 contour, h 表示  hole.

opencv 如何生成 contour 的 hierarchy? 个人认为（暂时没有研究 opencv 具体实现），一种可行的思路是使用区域增长，大概流程如下：

1）将种子点设置在图像边角处，使用背景颜色进行区域增长，区域增长在前景处停止；

2）使用形态学算子对当前增长后区域进行 dilate 操作，使 c0, c1,... 层级上的 contours 包含在当前增长区域中；

3）继续使用前景对图像增长，将 h00, h01,..., h10, h11,... 等层级上的 contours 包含在当前增长区域中；

4）如此循环，即可生成 contour 的  hierarchy 结构。

要使用 vector<cv::Vec4i> 表示 以上树形结构，每个 cv::Vec4i 元素值含义如下：

1) index 0: next contour(same level);

2) index 1: privous contour(same level);

3) index 2: first child(next level down);

4) index 3: parent(next level up);

参数 mode 表示如何提取 contours, 具体如下：

1) cv::PETR_EXTERNAL: 仅提取最外层 contour, 在以上图例中，仅提取 c0；

2) cv::PETR_LIST: 提取所有 contours, 组成链表结构，在图例中为: c010->c001->c000->h01->h00->c0；

3) cv::PETR_CCOMP: 提取所有 contours, 根据类型组成  hole list 和 contour list， 在图例中为：c010->c001->c000->c0, h01->h00, c0->h01(此处将前两个链表连接起来)；

4) cv::PETR_TREE: 提取所有 contours, 建立树形结构。

参数 method 对 contour 压缩，以减少数据量，包括：

1) cv::CHAIN_APPROX_NONE: 不做任何压缩；

2) cv::CHAIN_APPROX_SIMPLE: 压缩水平，垂直，对角方向上的线段；

4) cv::CHAIN_APPROX_TC89_L1/cv::CHAIN_APPROX_TC89_KCOS: 使用曲线曲率信息做更复杂的压缩。

参数 offset 将 contour 平移，在使用ROI进行 contour 提取时， 通过设置不同 offset 可以很方便的将 contour 绘制在原图上。

二  Contour Drawing

使用 cv::drawContours() 在图像上绘制 contours, 具体定义如下：

void cv::drawContours(cv::InputOutputArray image,

cv::InputArrayofArrays contours,

int contourIdx,

const cv::Scalar& color,

int thickness = 1,

int lineType = 8,

cv::InputArray hierarchy = noArray(),

int maxLevel = INT_MAX(),

cv::Point offset = cv::Point());

参数 image 为需要绘制 contours 图像。

参数 contours 为 cv::findContours() 生成。

参数 contourIdx 选择需要绘制的 contour, 如果其值为 -1， 则绘制所有 contours。

参数 color thickness lineType 分别定义线条颜色，线条宽度，线条类型(4连接 cv::LINE_4， 8连接 cv::LINE_8， 反走样cv::LINE_AA)。

参数 hierarchy maxLevel 共同控制 contours 层级。

参数 offset 表示绘制时平移值。

三 Contour Operation

1 cv::approxPolyDP() 对  contour 进行多边形近似，具体定义如下：

void cv::approxPolyDP(cv::InputArray curve, cv::OutputArray approxCurve, double epsilon, bool closed);

参数 curve 可以是 vector<cv::Point>, vector<cv::Point2f>  或者 arrays of size N*2, arrays of size N*1 with 2 channels。

参数 epsilon 表示近似精度，一般通过 contour 长度的百分比计算得出。

参数 closed 表示 contour 是否闭合。

cv::approxPolyDP() 函数使用 Douglas-Peucker approximation，基本思路如下：

1）在 contour 上寻找距离最大的两个点，将 contour 一分为二， 并连接两点构成线段S;

2)  在两个半边缘上分别寻找到到线段S上的最远点，将半边缘一分为二，连接以上四个点形成四边形；

3）继续寻找到四边形各条边上的最远点，构成多边形，知道最远点到对应边上距离小于epsilon停止。

2 double cv::arcLength(cv::InputArrray points, bool closed) 求 contour 长度。

3 double cv::contourArea(cv::InputArray points, bool oriented = false) 使用格林公式求 contour 所围成的面积，oriented = true 时返回带符号面积值，该函数对复杂区域（如自交区域）将返回错误结果。

4 cv::Rect cv::boundingRect(cv::InputArray points) 求 contour 所围成的矩形（无旋转矩形）。

5 cv::RotateRect cv::minAreaRect(cv::InputArray points) 求 contour 所围成的最小矩形（旋转矩形）。

6 void cv::minEnclosingCircle(cv::InputArray points, cv::Point2f& center, float& radius) 求 contour 所围成的最小圆形。

7 cv::RotateRect cv::fitEllipse(cv::InputArray points) 使用 contour 拟合椭圆（使用最小化代价函数）。

8 cv::fitLine() 拟合直线，具体定义如下：

void cv::fitLine(cv::InputArray points, cv::OutputArray line, int distType, double param, double reps, double aeps);

参数 points 接受二维或者三维点，拟合成二维平面直线或者三维空间直线。

参数 line 为 vec4f 或者 vec6f， 前两个（或三个）元素给出直线方向，后两个（或三个）给出直线上一个点。

参数  distType 表示距离度量范数，一般使用cv::DIST_L2, cv::DIST_L1。

参数 reps aeps 表示直线方向与直线点的计算精度，一般赋值为 .01 即可。

9 void cv::convexHull(cv::InputArray points, cv::OutputArray hull, bool clockwise = false, bool returnPoints = true) 计算 contour 凸包，凸包点集计算比较简单。

10 bool cv::isContourConvex(cv::InputArray contour) 判断  contour  凸性。

11 double cv::pointPolygonTest(cv::InputArray contour, cv::Point2f pt, bool measureDist) 判断点是否在 contour 中，如果 measureDist  = true, 返回点到最近边缘距离。

参考资料 Learning OpenCV 3   Adrian Kaehler & Gary Bradski