机器学习笔记—K-均值聚类

在聚类问题中，给定训练集 {x⁽¹⁾,...,x^(m)}，要把数据分成内聚的“簇”。这里 x⁽ⁱ⁾∈R，没有 y⁽ⁱ⁾。所以，这是一个无监督学习问题。

k-均值聚类算法如下：

1、随机初始化簇中心 μ₁,μ₂,...,μ_k∈Rⁿ；

2、重复直至收敛：{

对每个 i：

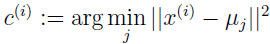
对每个 j：

}

其中 k 是簇个数，簇中心 μ_j 表示猜测的簇中心位置，初始化簇中心时，随机选择 k 个训练例子作为簇中心。

算法在内循环中不停执行两步：(i) 把每个 x⁽ⁱ⁾ 绑定到最近的簇中心 μ_j，(ii) 移动每个簇中心到相应簇的均值 μ_j。下图显示了 k均值的运行过程

k-均值算法保证收敛吗？在某种意义上，是的。特别的，我们定义畸变函数为：

J 表示每一个训练例和簇中心的距离平方。可以看出，k 均值就是 J 的坐标下降。特别的，k-均值的内循环不停地最小化 J，最小化 J 时， μ 固定时以 c 为参数，c 固定时以 μ 为参数，所以 J 一定是单调下降的，J 一定会收敛。通常，这意味着 c 和 μ 也会收敛。理论上，k-均值会在一些不同的聚类震荡，有相同的 J，但在实践中几乎不会发生。

畸变函数 J 是个非凸函数，所以 J 的坐标下降法不能保证收敛到全局最优，换句话说，k-均值可能会到局部最优。尽管如此，k-均值经常运行很好，可以得到很好的聚类结果。如果你还是担心陷入局部最优，一个常做的事情是多运行几次 k-均值算法（使用不同的随机初始值 μ_j），然后在找到的所有聚类结果中，选择 J 最小的一个结果。

参考资料：

1、http://cs229.stanford.edu/notes/cs229-notes7a.pdf