POJ 2663 Tri Tiling 矩阵快速幂 难度:3

Tri Tiling

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 7841		Accepted: 4113

Description

In how many ways can you tile a 3xn rectangle with 2x1 dominoes? 
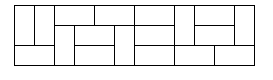
Here is a sample tiling of a 3x12 rectangle. 

Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 <= n <= 30.

Output

For each test case, output one integer number giving the number of possible tilings.

Sample Input

2
8
12
-1

Sample Output

3
153
2131

思路:只有八种转移状态,设初始状态为0(全空),得到状态7(111全染)

#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
typedef vector<long long > vec;
typedef vector<vec> mat;
const int mod=(1<<31-1);
mat mul(mat &A,mat &B){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++){
        for(int k=0;k<B.size();k++){
            for(int j=0;j<B[0].size();j++){
                C[i][j]=(C[i][j]+A[i][k]*B[k][j])%mod;
            }
        }
    }
    return C;
}
mat pow(mat A,long long n){
    mat B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++){
        B[i][i]=1;
    }
    while(n>0){
        if(n&1)B=mul(B,A);
        A=mul(A,A);
        n>>=1;
    }
    return B;
}
void calc(int m){
    mat m1(8,vec(8,0)),E(8,vec(8,0));
    E[0][7]=1;
    E[1][6]=1;
    E[2][5]=1;
    E[3][4]=1;
    E[4][3]=1;E[4][7]=1;
    E[5][2]=1;
    E[6][1]=E[6][7]=1;
    E[7][0]=1;E[7][4]=E[7][6]=1;
    E=pow(E,m);
    /*for(int i=0;i<E[0].size();i++){
        for(int j=0;j<E.size();j++){
            printf("%d ",E[i][j]);
        }
        puts("");
    }*/
    printf("%I64d\n",E[0][7]);
}
int main(){
    int m=0;
    while(scanf("%d",&m)==1&&m!=-1){
        calc(m+1);
    }
    return 0;
}