【JavaScript】数组随机排序 之 Fisher–Yates 洗牌算法

Fisher–Yates随机置乱算法也被称做高纳德置乱算法，通俗说就是生成一个有限集合的随机排列。Fisher-Yates随机置乱算法是无偏的，所以每个排列都是等可能的，当前使用的Fisher-Yates随机置乱算法是相当有效的，需要的时间正比于要随机置乱的数，不需要额为的存储空间开销。

一、算法流程：
需要随机置乱的n个元素的数组a：
for i 从n-1到1

j <—随机整数(0 =< j <= i)

交换a[i]和a[j]

end

二、实例

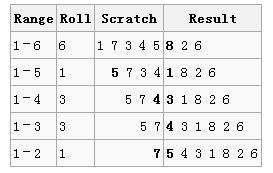
各列含义：范围、当前数组随机交换的位置、剩余没有被选择的数、已经随机排列的数

第一轮：从1到8中随机选择一个数，得到6，则交换当前数组中第8和第6个数

第二论：从1到7中随机选择一个数，得到2，则交换当前数组中第7和第2个数

下一个随机数从1到6中摇出，刚好是6，这意味着只需把当前线性表中的第6个数留在原位置，接着进行下一步；以此类推，直到整个排列完成。

截至目前，所有需要的置乱已经完成，所以最终的结果是：7 5 4 3 1 8 2 6

三、JS源代码

//算法思想：从0~i（i的变化为 n-1到0递减）中随机取得一个下标，和最后一个元素（i）交换。
function shuffle(arr) {
var i = arr.length, t, j;
while (i) {
j = Math.floor(Math.random() * i--); //!!!
t = arr[i];
arr[i] = arr[j];
arr[j] = t;
//console.log(arr);
}
return arr;
}

let arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, "J", "Q", "K", "A"];
undefined

for (let i = 0; i < 100; i ++) {
shuffle(arr)
}

四、潜在的偏差

在实现Fisher-Yates费雪耶兹随机置乱算法时，可能会出现偏差，尽管这种偏差是非常不明显的。原因：一是实现算法本身出现问题；二是算法基于的随机数生成器。

1.实现上每一种排列非等概率的出现

在算法流程里 j 的选择范围是从0...i-1；这样Fisher-Yates算法就变成了Sattolo算法，共有（n-1)!种不同的排列，而非n!种排列。

j在所有0...n的范围内选择，则一些序列必须通过n^n种排列才可能生成。

2.Fisher-Yates费雪耶兹算法使用的随机数生成器是PRNG伪随机数生成器

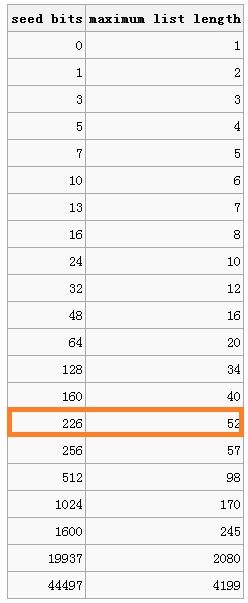
这样的一个伪随机数生成器生成的序列，完全由序列开始的内部状态所确定，由这样的一个伪随机生成器驱动的算法生成的不同置乱不可能多于生成器的不同状态数，甚至当可能的状态数超过了排列，不正常的从状态数到排列的映射会使一些排列出现的频率超过其他的。所以状态数需要比排列数高几个量级。

很多语言或者库函数内建的伪随机数生成器只有32位的内部状态，意味着可以生成2^32种不同的序列数。如果这样一个随机器用于置乱一副52张的扑克牌，只能产生52！ = 2^225.6种可能的排列中的一小部分。对于少于226位的内部状态的随机数生成器不可能产生52张卡片的所有的排列。

伪随机数生成器的内部状态数和基于此生成器的每种排列都可以生成的最大线性表长度之间的关系：

/**
 * Randomize array element order in-place.
 * Using Durstenfeld shuffle algorithm.
 */
function shuffleArray(array) {
    for (var i = array.length - 1; i > 0; i--) {
        var j = Math.floor(Math.random() * (i + 1));
        var temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }
    return array;
}

//使用ES2015（ES6）

Array.prototype.shuffle = function() {
  let m = this.length, i;
  while (m) {
    i = (Math.random() * m--) >>> 0;
    [this[m], this[i]] = [this[i], this[m]]
  }
  return this;
}