POJ 1458 最长公共子序列

子序列就是子序列中的元素是母序列的子集，且子序列中元素的相对顺序和母序列相同。

题目要求便是寻找两个字符串的最长公共子序列。

dp[i][j]表示字符串s1左i个字符和s2左j个字符的公共子序列的最大长度。

注意s1第i个字符为s1[i-1]

于是有递推公式：

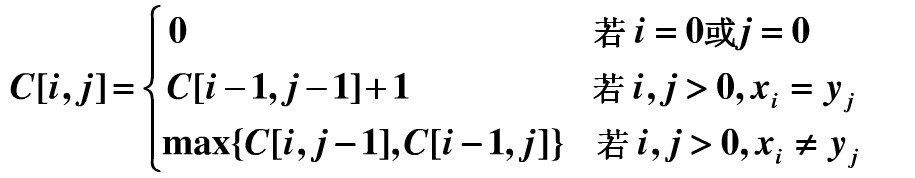
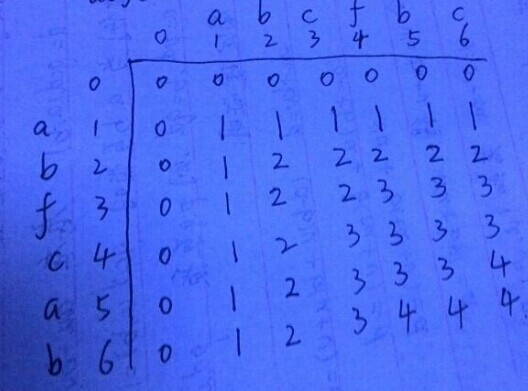
对于abcfbc和abfcab两个字符串，求公共子串的最大长度的过程如图：

 //#define LOCAL
 #include <iostream>
 #include <cstdio>
 #include <cstring>
 using namespace std;

 const int maxn = ;
 char s1[maxn], s2[maxn];
 int dp[maxn][maxn];

 int main(void)
 {
     #ifdef LOCAL
         freopen("1458in.txt", "r", stdin);
     #endif

     while(cin >> s1 >> s2)
     {
         int Lenth1 = strlen(s1);
         int Lenth2 = strlen(s2);
         memset(dp, , sizeof(dp));

         int i, j;
         for(i = ; i <= Lenth1; ++i)
             for(j = ; j <= Lenth2; ++j)
             {
                 if(s1[i-] == s2[j-])
                     dp[i][j] = dp[i-][j-] + ;
                 else
                     dp[i][j] = max(dp[i-][j], dp[i][j-]);
             }

         printf("%d\n", dp[Lenth1][Lenth2]);
     }
     return ;
 }

代码君