【BZOJ1007】【HNOI2008】水平可见直线

依旧看黄学长代码，不过这回是看完后自己写的

原题：

在xoy直角坐标平面上有n条直线L1,L2,...Ln,若在y值为正无穷大处往下看,能见到Li的某个子线段,则称Li为
可见的,否则Li为被覆盖的.
例如,对于直线:
L1:y=x; L2:y=-x; L3:y=0
则L1和L2是可见的,L3是被覆盖的.
给出n条直线,表示成y=Ax+B的形式(|A|,|B|<=500000),且n条直线两两不重合.求出所有可见的直线.

0 < N < 50000

给线段求下凸包，还算比较简单把

用栈，首先根据斜率排个序，这里建议如果斜率相等呢么y轴上截距递减，这样如果要插入的直线斜率和栈顶斜率相等直接停止就行了

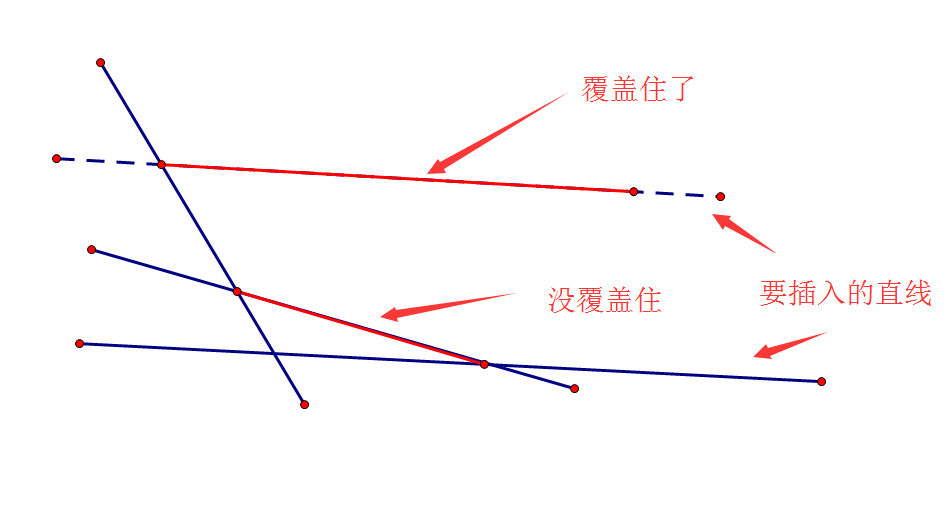
如果要插入的直线和栈中top-1的交点在栈中top和栈中top-2的交点的左边，呢么top--

为什么呐

手玩三条直线很容易看出来，图比较好画我就画一下吧（我也只能画简单的图了）

怎么计算交点呐

因为是很简单的x=kx+b，这就是小学数学，为了增加文章的篇幅来扯一扯 _(:3 」∠)_

就是解二元一次方程组，{y=k1x+b1,y=k2x+b2}，下面减上面，(k2-k1)x=b1-b2，x=(b1-b2)/(k2-k1)

然后随便搞一搞就行了，最后用bool记录答案来保证id递增

小技巧：fabs是计算浮点数的绝对值，注意fabs计算的并不是差的绝对值，也就是说应该是fabs(a-b)而不是fabs(a,b)，需要cmath

我看黄学长和另一个人的代码比x的时候都是直接<=，算时x返回是double啊不是不能直接=么，然而还是过了，不知道为什么

代码：

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 using namespace std;
 int read(){int z=,mark=;  char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')mark=-;  ch=getchar();}
     while(ch>=''&&ch<=''){z=(z<<)+(z<<)+ch-'';  ch=getchar();}
     return z*mark;
 }
 bool deng(double x,double y){  return fabs(x-y)<1e-;}//fabs传的是绝对值，所以不能fabs(a-b)
 int n;  struct cdd{double k,b;  int id;}a[];//y=kx+b
 bool compare(cdd x,cdd y){  return (deng(x.k,y.k)) ? (x.b>y.b) : (x.k<y.k);}
 bool ans[];
 cdd zhan[];  int top=;
 double get_x(cdd x,cdd y){  return (x.b-y.b)/(y.k-x.k);}
 void insert(cdd x){
     if(deng(x.k,zhan[top].k))  return ;
     while(top> && get_x(x,zhan[top-]) <= get_x(zhan[top],zhan[top-]))  top--;
     zhan[++top]=x;
 }
 int main(){//freopen("ddd.in","r",stdin);
     memset(ans,,sizeof(ans));
     cin>>n;
     for(int i=;i<=n;i++)  scanf("%lf%lf",&a[i].k,&a[i].b),a[i].id=i;
     sort(a+,a+n+,compare);
     a[].k=a[].b=-;
     for(int i=;i<=n;i++)  insert(a[i]);
     for(int i=;i<=top;i++)  ans[zhan[i].id]=true;
     for(int i=;i<=n;i++)if(ans[i])  printf("%d ",i);
     cout<<endl;
     return ;
 }