【题解】【矩阵】【回溯】【Leetcode】Unique Paths II

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

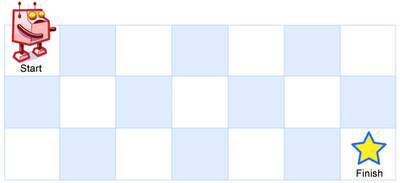
Above is a 3 x 7 grid. How many possible unique paths are there?

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

For example,

There is one obstacle in the middle of a 3x3 grid as illustrated below.

[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]

The total number of unique paths is 2.

Note: m and n will be at most 100.

思路：

很典型的回溯问题，到[i,j]的路径等于到[i-1,j]和[i,j-1]的路径之和，然后为了避免重复求解子问题，结合查表法记录子问题结果。编码要点在于处理 trivial case。

代码：

 int uniquePaths2Node(vector<vector<int> > &oGrid, vector<vector<int> > &paths, int i, int j){
     //if(i < 0 || j < 0) return 0;//failed [[1]]=>0, 应该把控制条件放下面，不给调用不valid的子问题
     if(oGrid[i][j] == ) return ;

     if(i ==  && j == ) return  ^ oGrid[][];//failed [[0]]=>1

     int P = ;
     if(i >  && oGrid[i-][j] != ){
         if(paths[i-][j] == -)
             paths[i-][j] = uniquePaths2Node(oGrid, paths, i-, j);
         P += paths[i-][j];
     }
     if(j >  && oGrid[i][j-] != ){
         if(paths[i][j-] == -)
             paths[i][j-] = uniquePaths2Node(oGrid, paths, i, j-);
         P += paths[i][j-];
     }
     return P;
 }
 int uniquePathsWithObstacles(vector<vector<int> > &obstacleGrid) {
     int m = obstacleGrid.size();
     if(m == ) return ;
     int n = obstacleGrid[].size();
     if(n == ) return ;

     vector<vector<int> > paths(m, vector<int>(n, -));
     return uniquePaths2Node(obstacleGrid, paths, m-, n-);
 }