CF 500 B. New Year Permutation 并查集

User ainta has a permutation p1, p2, ..., pn. As the New Year is coming, he wants to make his permutation as pretty as possible.

Permutation a1, a2, ..., an is prettier than permutation b1, b2, ..., bn, if and only if there exists an integer k (1 ≤ k ≤ n) wherea1 = b1, a2 = b2, ..., ak - 1 = bk - 1 and ak < bk all holds.

As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n × n binary matrix A, user ainta can swap the values of pi and pj (1 ≤ i, j ≤ n,i ≠ j) if and only if Ai, j = 1.

Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.

Input

The first line contains an integer n (1 ≤ n ≤ 300) — the size of the permutation p.

The second line contains n space-separated integers p1, p2, ..., pn — the permutation p that user ainta has. Each integer between 1 and n occurs exactly once in the given permutation.

Next n lines describe the matrix A. The i-th line contains n characters '0' or '1' and describes the i-th row of A. The j-th character of the i-th line Ai, j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i, j where 1 ≤ i < j ≤ n, Ai, j = Aj, i holds. Also, for all integers i where 1 ≤ i ≤ n, Ai, i = 0 holds.

Output

In the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.

Sample test(s)

input

7
5 2 4 3 6 7 1
0001001
0000000
0000010
1000001
0000000
0010000
1001000

output

1 2 4 3 6 7 5

input

5
4 2 1 5 3
00100
00011
10010
01101
01010

output

1 2 3 4 5

Note

In the first sample, the swap needed to obtain the prettiest permutation is: (p1, p7).

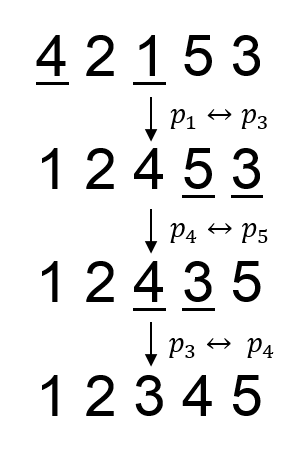
In the second sample, the swaps needed to obtain the prettiest permutation is (p1, p3), (p4, p5), (p3, p4).

A permutation p is a sequence of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. The i-th element of the permutation p is denoted as pi. The size of the permutation p is denoted as n.

题意：

给出一个序列，长度为n

然后是n*n的矩阵，矩阵的值为0或者1

maze[i][j]=1表示序列第i个和序列第j个可以交换

maze[i][j]=0表示序列第i个和序列第j个不可以交换

矩阵保证maze[i][j]=maze[j][i]

现在你可以进行操作：若2个数可以交换，你可以交换他们，也可以不交换

你可以操作无限次

问最后得到的最小序列是多少？

2个序列，若第一个不相等的数越小，该序列越小

并查集，把可以交换的那一堆位置的值放在一起

对于序列第i个位置，找到i属于哪一堆，再从这一堆中还没有用过的数中挑出一个最小的数，放在第i的位置。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>

 using namespace std;

 const int maxn=;
 const int inf=0x3f3f3f3f;
 int ans[maxn][maxn];    //第i堆数的值
 int iter[maxn];         //现在第i堆数中要拿的数是第iter[i]个，即这一堆中还没有用过的数中的最小值是第iter[i]个
 int fa[maxn];           //并查集
 int init[maxn];         //存放初始序列的值
 int num[maxn];          //第i个位置属于第num[i]堆
 int print[maxn];        //存放最后的序列，方便输出
 int len[maxn];          //第i堆数有len[i]个
 char str[maxn];         //方便输入数据

 int find_fa(int x)
 {
     if(fa[x]==x)
         return x;
     else
         return fa[x]=find_fa(fa[x]);
 }

 int main()
 {
     int n;
     scanf("%d",&n);
     for(int i=;i<=n;i++){
         for(int j=;j<=n;j++)
             ans[i][j]=inf;
     }

     for(int i=;i<=n;i++)
         scanf("%d",&init[i]);
     for(int i=;i<=n;i++)
         fa[i]=i;
     for(int i=;i<=n;i++){
         scanf("%s",str);
         for(int j=;j<=n;j++){
             int u=str[j-]-'';
             if(u>){
                 int fai=find_fa(i);
                 int faj=find_fa(j);
                 if(fai!=faj)
                     fa[faj]=fai;
             }
         }
     }
     //printf("eee\n");
     for(int i=;i<=n;i++){
         len[i]=;
         num[i]=-;
     }
     int tot=;
     for(int i=;i<=n;i++){
         int cnt=find_fa(i);
         if(num[cnt]>){
             num[i]=num[cnt];
             ans[num[i]][len[num[i]]++]=init[i];
         }
         else{
             num[cnt]=tot;
             num[i]=tot;
             ans[tot][len[tot]++]=init[i];
             tot++;
         }
     }
     for(int i=;i<tot;i++){
         sort(ans[i]+,ans[i]+len[i]);
     }
     for(int i=;i<tot;i++)
         iter[i]=;
     for(int i=;i<=n;i++){
         print[i]=ans[num[i]][iter[num[i]]++];
     }
     for(int i=;i<n;i++)
         printf("%d ",print[i]);
     printf("%d\n",print[n]);

     return ;
 }