KMP算法初探
[edit by xingoo]
kmp算法其实就是一种改进的字符串匹配算法。复杂度可以达到O(n+m),n是参考字符串长度,m是匹配字符串长度。
传统的算法,就是匹配字符串与参考字符串挨个比较,如果相同就比较下一个,如果不相同,就返回上一次的结果,再重新比较。
如图1 如果失败则字符串会重新用S(参考字符串)的第二个,与T(匹配字符串)的第一个比较,知道全部符合查找,或找不到为止。
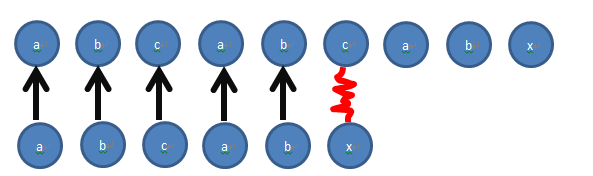
此时发现S[5] != T[5],因此用S[1]与T[0]进行比较。

此时发现S[1]!=T[0],因此用S[2]与T[0]比较。

此时,仍然不相等,继续后移。
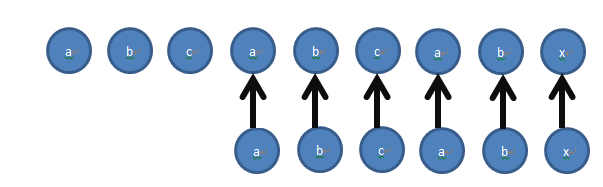
此时,S[3] == T[0],继续比较,发现所有T元素都在S中找到,满足查找,返回开始匹配的下标3.
传统代码
int old_index(char * S,char * T){
int i=;
int j=;
while(i<strlen(S) && j<strlen(T)){
if( S[i] == T[j] ){
++i;
++j;
}
else{
i = i-j+; //上一次的下一个
j=;
}
}
if(j == strlen(T))
return i-strlen(T);
else
return -;
}
这种比较忽略了一个问题,就是在T中,abcabx,第一个字符串因为不跟第二个,第三个一样,因此,在一开始的匹配中,可以直接跳过比较,直接从S的第三个元素开始比较。这里就涉及到一个概念:最短子串对称匹配。

首先,初始化,当j=0时,next(j)=-1;
当j=1时,字符串0到j-1,只有"a",因此 next(j) = 0;
当j=2时,字符串0到j-1,字符串为"ab",因此next(j) = 0;
当j=3时,字符串0到j-1,字符串为"abc",因此next(j) = 0;
当j=4时,字符串0到j-1,字符串为"abca",此时,前缀a在末尾出现,因此next(j) = 1;
当j=5时,字符串0到j-1,字符串为"abcab",此时,前缀ab在末尾出现,因此next(j) = 2;
最后得到next的数组为"-1 0 0 0 1 2"。
按照这个方法:
ababab的next数组为"-1 0 0 1 2 3 4"
这里面,当j=5时,字符串"ababa",前缀是"aba",后缀也是"aba",因此next值为3.
计算next数组详细代码
void getNext(char * T,int *next){
int i,j;
i=;
j=-;
next[]=-;
while(i<strlen(T)){
if(j == - || T[i] == T[j]){
++i;
++j;
next[i] = j;
}
else{
j = next[j];
}
}
}
kmp匹配代码
int kmp(char* S,char * T){
int i=;
int j=;
int next[MAX];
getNext(T,next);
while(i<strlen(S) && j<strlen(T)){
printf("i %d-%c j %d-%c\n",i,S[i],j,T[j]);
if(j== || S[i]==T[j]){
++i;
++j;
}else{
j = next[j];
printf("j back to %d\n",j);
}
}
if(j == strlen(T))
return i-strlen(T);
else
return ;
}
全部代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX 20 void getNext(char * T,int *next);
int kmp(char * S,char * T);
int old_index(char * S,char * T); int main()
{
char * s = "acabbabababc";
char * t = "ababab"; //printf("the pos is:%d\n\n",old_index(s,t));
//printf("the pos is:%d\n\n",old_index(m,t));
//printf("the pos is:%d\n\n",old_index(n,t));
printf("the pos is:%d\n",kmp(s,t));
return ;
} void getNext(char * T,int *next){
int i,j;
i=;
j=-;
next[]=-;
while(i<strlen(T)){
if(j == - || T[i] == T[j]){
++i;
++j;
next[i] = j;
}
else{
j = next[j];
}
}
} int kmp(char* S,char * T){
int i=;
int j=;
int next[MAX];
getNext(T,next);
while(i<strlen(S) && j<strlen(T)){
printf("i %d-%c j %d-%c\n",i,S[i],j,T[j]);
if(j== || S[i]==T[j]){
++i;
++j;
}else{
j = next[j];
printf("j back to %d\n",j);
}
}
if(j == strlen(T))
return i-strlen(T);
else
return ;
}
int old_index(char * S,char * T){
int i=;
int j=;
while(i<strlen(S) && j<strlen(T)){
if( S[i] == T[j] ){
++i;
++j;
}
else{
i = i-j+; //上一次的下一个
j=;
}
}
if(j == strlen(T))
return i-strlen(T);
else
return -;
}
运行结果
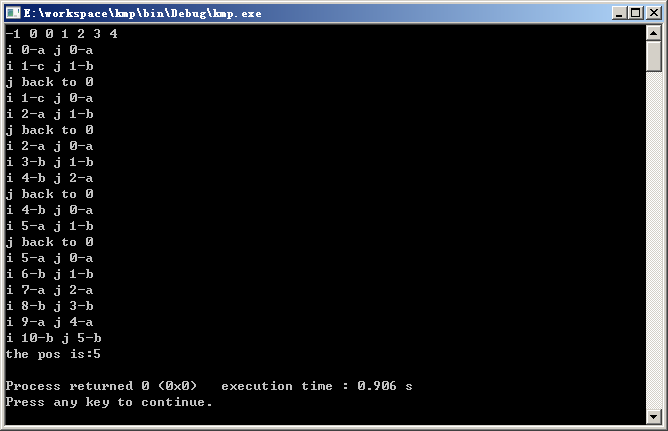
KMP算法初探的更多相关文章
- 初探KMP算法
数据结构上老师也没讲这个,平常ACM比赛时我也没怎么理解,只是背会了代码--前天在博客园上看见了一篇介绍KMP的,不经意间就勾起了我的回忆,写下来吧,记得更牢. 一.理论准备 ...
- 简单有效的kmp算法
以前看过kmp算法,当时接触后总感觉好深奥啊,抱着数据结构的数啃了一中午,最终才大致看懂,后来提起kmp也只剩下“奥,它是做模式匹配的”这点干货.最近有空,翻出来算法导论看看,原来就是这么简单(先不说 ...
- KMP算法
KMP算法是字符串模式匹配当中最经典的算法,原来大二学数据结构的有讲,但是当时只是记住了原理,但不知道代码实现,今天终于是完成了KMP的代码实现.原理KMP的原理其实很简单,给定一个字符串和一个模式串 ...
- 萌新笔记——用KMP算法与Trie字典树实现屏蔽敏感词(UTF-8编码)
前几天写好了字典,又刚好重温了KMP算法,恰逢遇到朋友吐槽最近被和谐的词越来越多了,于是突发奇想,想要自己实现一下敏感词屏蔽. 基本敏感词的屏蔽说起来很简单,只要把字符串中的敏感词替换成"* ...
- KMP算法实现
链接:http://blog.csdn.net/joylnwang/article/details/6778316 KMP算法是一种很经典的字符串匹配算法,链接中的讲解已经是很明确得了,自己按照其讲解 ...
- 数据结构与算法JavaScript (五) 串(经典KMP算法)
KMP算法和BM算法 KMP是前缀匹配和BM后缀匹配的经典算法,看得出来前缀匹配和后缀匹配的区别就仅仅在于比较的顺序不同 前缀匹配是指:模式串和母串的比较从左到右,模式串的移动也是从 左到右 后缀匹配 ...
- 扩展KMP算法
一 问题定义 给定母串S和子串T,定义n为母串S的长度,m为子串T的长度,suffix[i]为第i个字符开始的母串S的后缀子串,extend[i]为suffix[i]与字串T的最长公共前缀长度.求出所 ...
- 字符串模式匹配之KMP算法图解与 next 数组原理和实现方案
之前说到,朴素的匹配,每趟比较,都要回溯主串的指针,费事.则 KMP 就是对朴素匹配的一种改进.正好复习一下. KMP 算法其改进思想在于: 每当一趟匹配过程中出现字符比较不相等时,不需要回溯主串的 ...
- 算法:KMP算法
算法:KMP排序 算法分析 KMP算法是一种快速的模式匹配算法.KMP是三位大师:D.E.Knuth.J.H.Morris和V.R.Pratt同时发现的,所以取首字母组成KMP. 少部分图片来自孤~影 ...
随机推荐
- xsheell的下载安装初级使用
1)关于Xshell 网上更多的资料里提到的SSH客户端是putty,因为简单.开源.免费.但是也正是由于功能过于简单,所以在这里推荐大家使用Xshell. Xshell最初并不能免费使用,而且也没有 ...
- JSTL标签用法 详解
在JSP的开发中,迭代是经常要使用到的操作.例如,逐行的显示查询的结果等.在早期的JSP中,通常使用Scriptlets来实现Iterator或者Enumeration对象的迭代输出.现在,通过JST ...
- linux下valgrind的使用概述
Valgrind简介: Valgrind是动态分析工具的框架.有很多Valgrind工具可以自动的检测许多内存管理和多进程/线程的bugs,在细节上剖析你的程序.你也可以利用Valgrind框架来实现 ...
- [Papers]NSE, $u$, Lorentz space [Bosia-Pata-Robinson, JMFM, 2014]
$$\bex \bbu\in L^p(0,T;L^{q,\infty}),\quad \frac{2}{p}+\frac{3}{q}=1,\quad 3<q\leq\infty. \eex$$ ...
- ScrollView中嵌套ListView
scrollview中嵌入listview,要是直接把listview嵌进scrollview中,listview的高度是固定的不能进行滑动.默认情况下Android是禁止在ScrollView中放入 ...
- SqlDataReader对象的NextResult方法读取存储过程多个结果集
如上图,我这里有返回4个记录集,分别表示 发送的总数,成功数,失败数,以及所有的记录集,那么我怎么去获取呢? 如果我第二个记录集 第三个记录集 都是多行的话,怎么办?可以参考下面这张图
- html --- canvas --- javascript --- 拖拽圆圈
代码如下: <!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <tit ...
- cocos2dx 水波纹Shader
// on "init" you need to initialize your instance bool HelloWorld::init() { ////////////// ...
- 【JNI】OPUS压缩与解压的JNI调用(.DLL版本)
OPUS压缩与解压的JNI调用(.DLL版本) 一.写在开头: 理论上讲,这是我在博客园的第一篇原创的博客,之前也一直想找个地方写点东西,把最近做的一些东西归纳总结下,但是一般工程做完了一高兴就把东西 ...
- Ansible的循环
Ansible的循环 1. 前言 有可能在一个任务中,可能要做很多事情,例如创建多个用户,安装很多个包等,那么就有可能用到循环. 2. 标准循环 重复的任务可以用下面的方式: ...
