频繁项集挖掘之Aprior和FPGrowth算法

频繁项集挖掘的应用多出现于购物篮分析，现介绍两种频繁项集的挖掘算法Aprior和FPGrowth，用以发现购物篮中出现频率较高的购物组合。

基础知识

　　项：“属性-值”对。比如啤酒2罐。 
　　项集：项的集合。比如{啤酒2罐，…，尿布5片} 
　　K项集：项集中的每个项都有K个项。 
　　支持度：项集在训练元组中同时出现的次数（或者比例）。 
　　置信度：A−>BA−>B的置信度，表示P(B|A)P(B|A)，是个条件概率。（置信度大于用户规定的最小置信度的规则是可信的） 
　　兴趣度：A−>BA−>B的置信度与BB的整体占比的差值。兴趣度越大，表示AA对BB的出现起到的促进作用越大。为负值时表示起到的抑制作用。为0时表示没有影响。 
　　子集：被包含于某项集的项集。 
　　超集：能包含某项集的项集。 
　　频繁项集：在训练元组中，同时出现次数超过支持度的项集。 
　　极大频繁项集：对当前频繁项集来说，没有包含它的频繁超集，则称当前项集为极大频繁超集。

Aprior算法

　　Aprior算法的基本思想是由KK项频繁项集产生K+1K+1项频繁项集，直到满足条件的频繁项集发现为止。

连接定理和频繁子集定理

　　连接定理：解决如何由KK项集产生K+1K+1项集问题。若有两个KK项集，其前K−1K−1个项是相同的，则这两个项集可以连接产生一个K+1项集。 
　　频繁子集定理：用来压缩搜索空间。若一个项集的子集不是频繁项集，则该项集也不是频繁项集。（换句话说，非频繁项集的超集也是非频繁项集；频繁项集的所有非空子集也都是频繁项集）

Aprior算法步骤

　　1. 扫描数据库，产生候选1项集和频繁项集。 
　　2. 从2项集开始循环，由频繁K-1项集生成频繁K项集。 
　　2.1 产生候选项集。根据连接定理，产生候选项集（有个排序的要求，加快比较）。 
　　2.2 去掉非频繁项集。根据频繁子集定理产生频繁项集。 
　　2.3 去掉不符合条件的项集。扫描数据库，计算支持度、置信度、兴趣度，去掉不符合条件的项集。（这地方可变） 
　　2.4 判断迭代终止条件。

Apriro优缺点

　　Aprior优点： 
　　1）对大型数据库的处理能力，不需要将数库读入内存就可以完成频繁项集的挖掘。 
　　Aprior缺点： 
　　1）需要多次扫描数据库，效率低下。

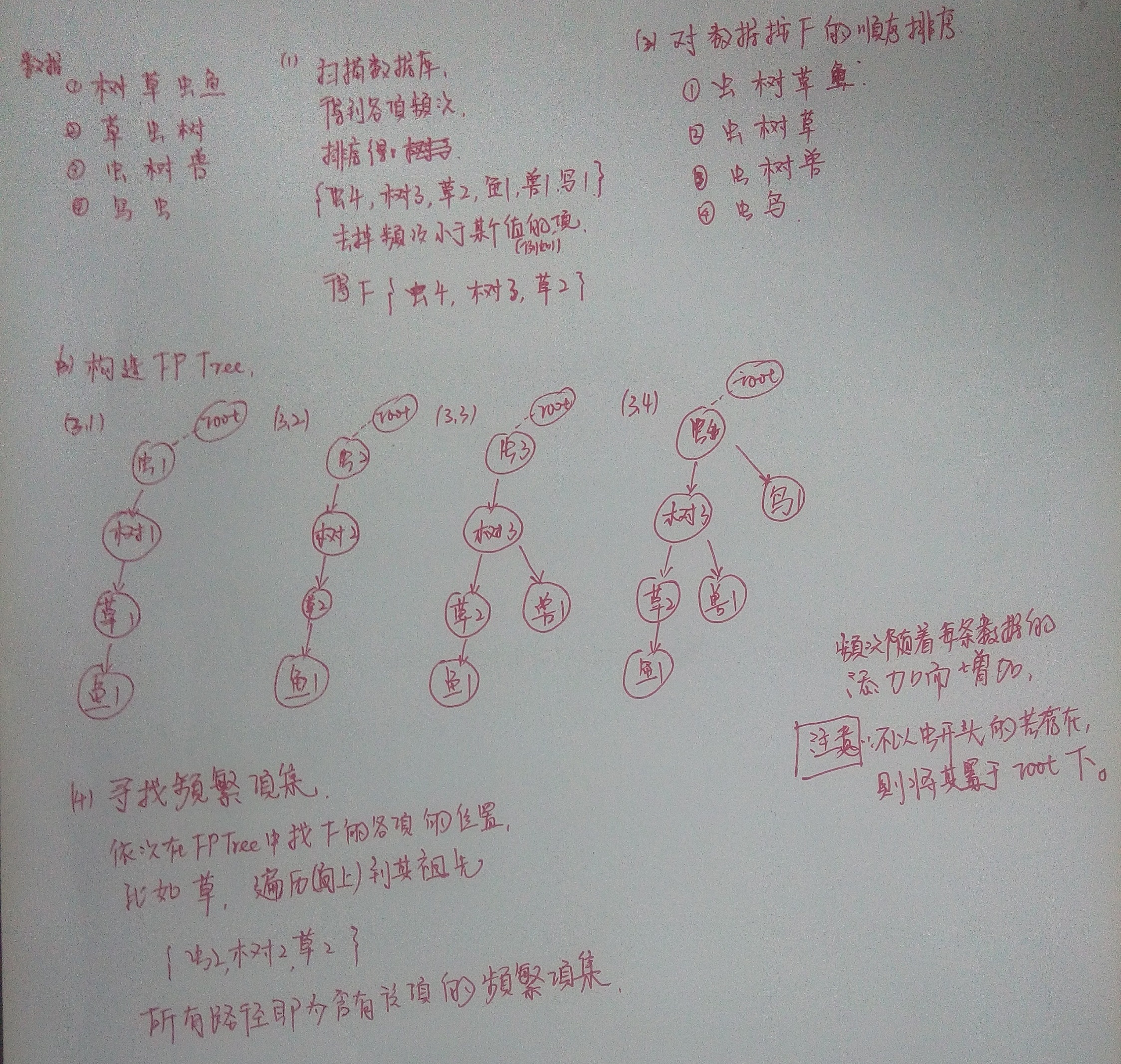
FPGrowth算法

　　FPGrowth的基本思想是将原始数据压缩到一个FPTree上，在该树上进行频繁项集的挖掘。（FPTree是共用前缀的）

FPGrowth算法步骤

　　
　　讲地非常好的FPGrowth算法博客（包括原理讲解和代码实现）： 
(1)http://blog.csdn.net/huagong_adu/article/details/17739247　　(2)http://www.cnblogs.com/zhangchaoyang/articles/2198946.html

FPGrowth优缺点

　　优点： 
　　1）只需要扫描两边数据库，效率高。 
　　2）可以并行化实现。 
　　缺点： 
　　1）受内存大小限制。