LdA笔记

　　LDA算法最初的论文使用的是变分EM方法训练（Variational Inference）。该方法较为复杂，而且最后训练出的topic主题非全局最优分布，而是局部最优分布。后期发明了Collapsed Gibbs Sample方法，推导和使用较为简洁。　　

　　Latent Dirichlet Allocation是Blei等人于2003年提出的基于概率模型的主题模型算法，LDA是一中非监督机器学习技术，可以用于识别大规模文档集或语料库中的潜在隐藏主题信息。该方法假设每个词由背后的一个潜在隐藏的主题中抽取出来。

1，Gamma函数-欧拉

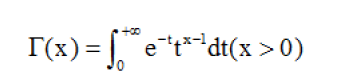
2，Binomial Distribution二项式分布-在概率论中，二项分布即重复n词独立的伯努利实验，是n重伯努利试验成功次数的离散概率分布。

伯努利分布(Bernoulli distribution)又名两点分布或0-1分布。

3，beta分布-在概率论中，beta分布是指一组定义在（0,1）的连续概率分布，有两个参数

4，Beta函数和Gamma函数的重要关系-第一欧拉积分

在介绍贝塔分布(Beta distribution)之前，需要先明确一下先验概率、后验概率、似然函数以及共轭分布的概念。

• 通俗的讲，先验概率就是事情尚未发生前，我们对该事发生概率的估计。利用过去历史资料计算得到的先验概率，称为客观先验概率； 当历史资料无从取得或资料不完全时，凭人们的主观经验来判断而得到的先验概率，称为主观先验概率。例如抛一枚硬币头向上的概率为0.5，这就是主观先验概率。
• 后验概率是指通过调查或其它方式获取新的附加信息，利用贝叶斯公式对先验概率进行修正，而后得到的概率。
• 先验概率和后验概率的区别：先验概率不是根据有关自然状态的全部资料测定的，而只是利用现有的材料(主要是历史资料)计算的；后验概率使用了有关自然状态更加全面的资料，既有先验概率资料，也有补充资料。另外一种表述：先验概率是在缺乏某个事实的情况下描述一个变量；而后验概率（Probability of outcomes of an experiment after it has been performed and a certain event has occured.）是在考虑了一个事实之后的条件概率。
• 似然函数：似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性。是指某种事件发生的可能性。给定输出x时，关于参数θ的似然函数L(θ|x)（在数值上）等于给定参数θ后变量X的概率：L(θ|x)=P(X=x|θ)。
• 共轭分布(conjugacy)：后验概率分布函数与先验概率分布函数具有相同形式

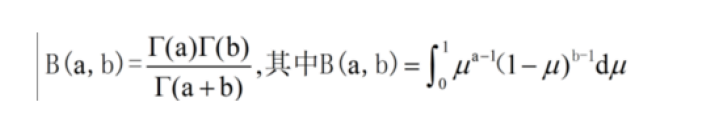
Beta分布的期望：

Dirichlet分布的期望：

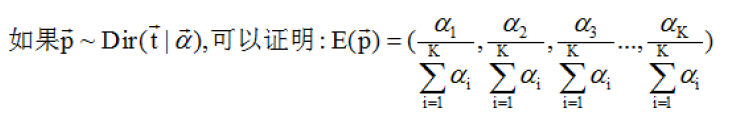
4，多项式分布-多项式分布是二项分布的推广，在n次独立实验中每次只输出k中结果中的一个，且每一种都有一个确定的概率p。多项分布给出了在多种输出状态的情况下，关于成功次数的各种组合的概率。

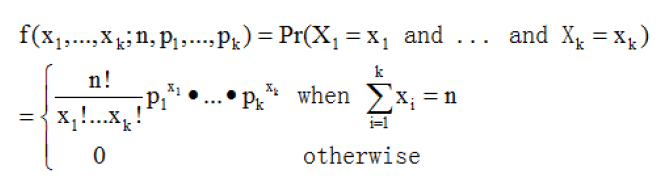
也可以用Gamma函数表示

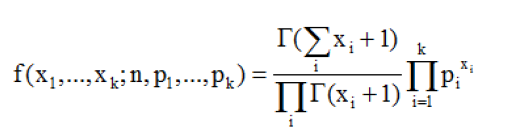
6，dirichlet distribution-狄利克雷分布

狄利克雷分布(Dirichlet distribution)是多项分布的共轭分布，也就是它与多项分布具有相同形式的分布函数。

dirichlet分布的概率密度函数：

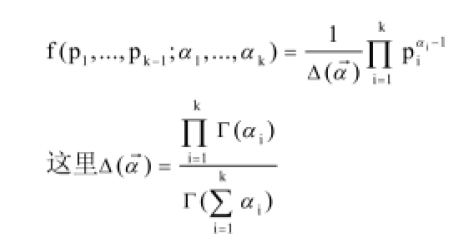
LDA详解：

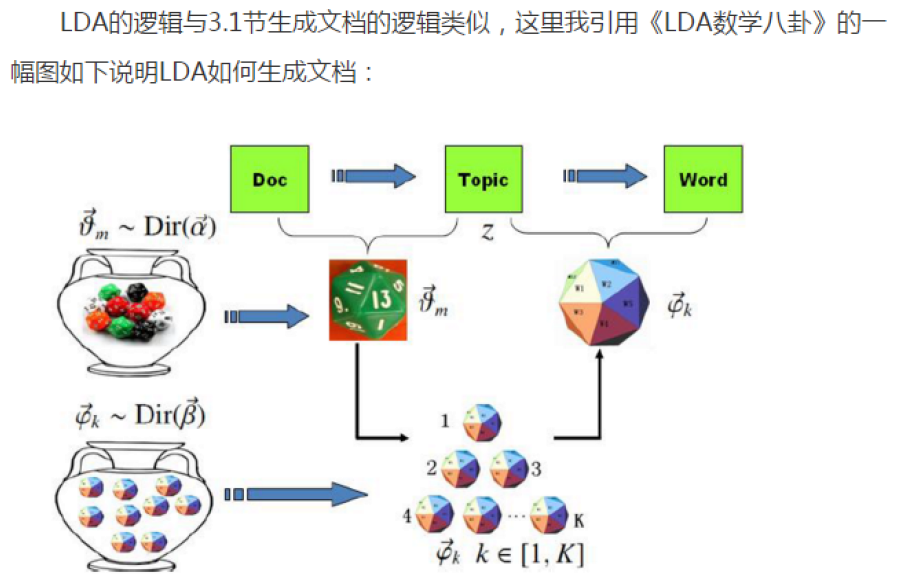
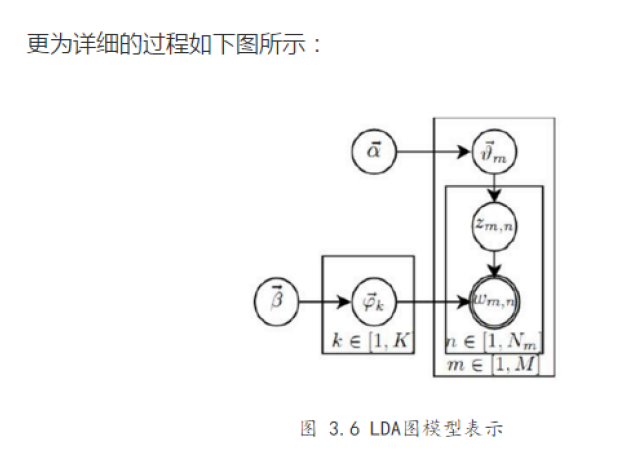
而LDA的目的是找出每个词后潜在的主题，所以为了达到这个目标，需要计算后验概率。

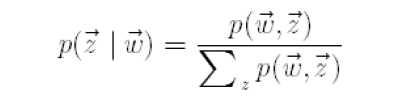
6，马尔可夫链-Markov Chain

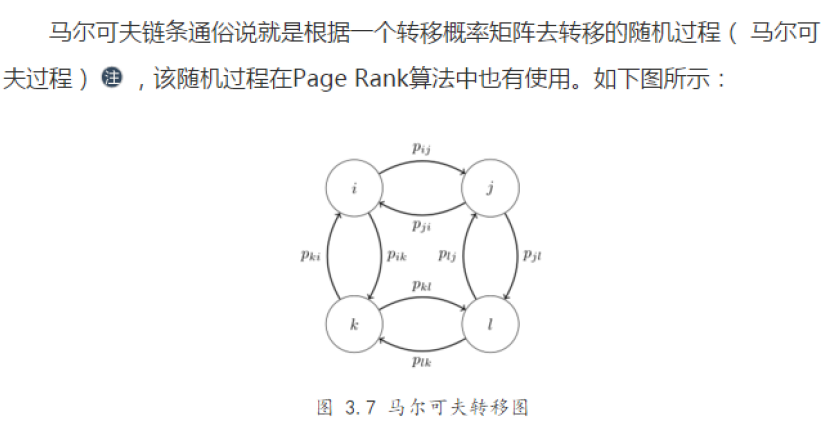
马尔可夫链要成为Reversible markov chain，需要满足Datailed balance(细致平稳），即其转移概率需要满足Kolmogorov's criterion的链条（柯尔莫哥洛夫准则），即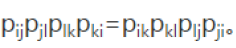

7，Metorpolis-Hasting算法

8，Gibbs Sampling

9，Gibbs迭代公式的推导

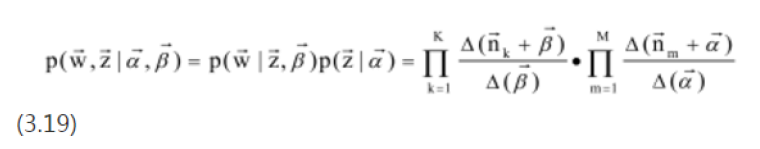
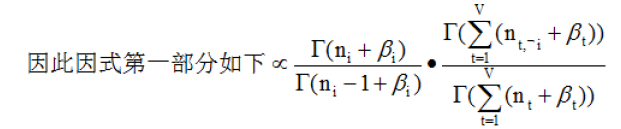
10，alpha和Beta的计算

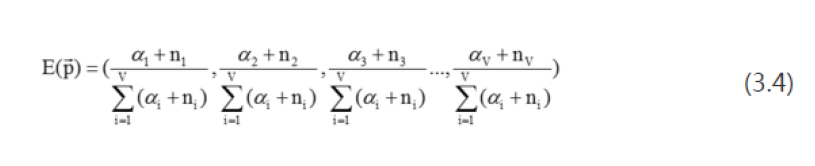
11，模型检验-困惑度函数

参考链接：http://blog.sina.com.cn/s/blog_4c9dc2a10102vua9.html

http://blog.csdn.net/luo123n/article/details/48902815