拉格朗日乘子法以及KKT条件

拉格朗日乘子法是一种优化算法，主要用来解决约束优化问题。他的主要思想是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有n+k个变量的无约束优化问题。

其中，利用拉格朗日乘子法主要解决的问题为：

等式的约束条件和不等式的条件约束。

拉格朗日乘子的背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。

等约束条件的解决方法不在赘述。

对于非等约束条件的求解，需要满足KKT条件才能进行求解。下面对于KKT条件进行分析。

不等式约束优化问题：

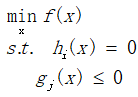
得到拉格朗日乘子法的求解方程：

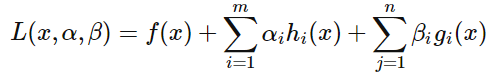
给出KKT条件：

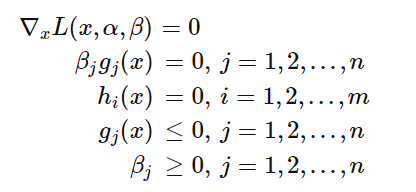
实际上，为什么要给出KKT条件？这里涉及到对偶问题。

我们引入拉格朗日函数L(x,α,β)将有约束的优化问题转换为无约束的优化问题，然后对原问题的参数求导，获得使拉格朗日函数最小的拉格朗日对偶函数g(α,β)，最后使得对偶函数最大的问题则成为原问题的对偶问题。（对偶函数给出了主问题最优解的下界。那么下界最大是什么，这就是主问题的对偶问题）

因此对于上面拉格朗日乘子法问题的描述表达为：

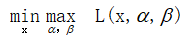
但其实是仍然个很难解决的问题，因为我们要先解决不等式约束的max问题，然后再在x上求最小值。怎么办呢？如果能把顺序换一下，先解决关于x的最小值，在解决关于α、β的不等式约束问题就好了。即，

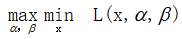
假设原问题为p，对偶问题为d，事实上，p和d并不完全相等，此处含有一个性质：弱对偶性

即：

而他两个的差即为对偶间隙

解释：大家想一下，函数L中最大值中最小的一个总比最小值中最大的那一个要大，也就是对偶问题提供了原问题最优值的一个下界。

但是大家想，我们是想通过对偶问题求解原问题的最优解，所以只有当二者相等时才可能将原问题转化成对偶问题进行求解。当然，当满足一定条件的情况下，便有p=d。而这个条件便是 slater条件和KTT条件。

在凸优化理论中，有一个Slater定理，当这个定理满足，结合KKT条件，那么对偶间隙就会消失，就是强对偶性成立。

其中对于KKT条件的KKT因子为什么需要大于等于0不太好理解。

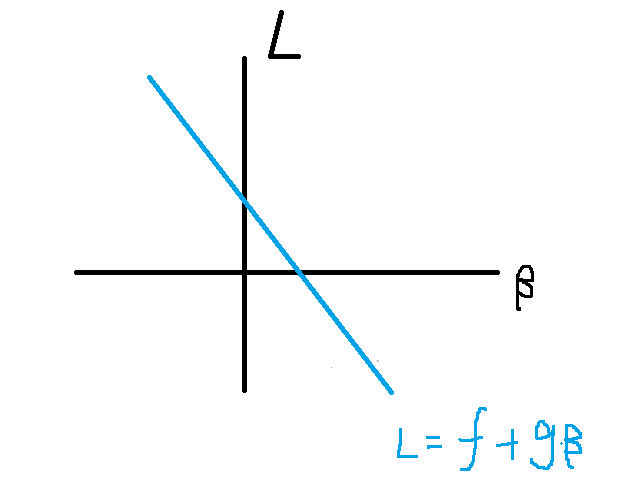
我的理解：如上，只有当大于等于0的时候，L的取值才能有最大值，即：

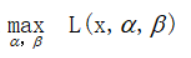这一步才有值。

当然这个只是我个人的理解吧，理论上详细的证明参考《数值优化》-Jorge Nocedal  第12章

当然它上面的公式：

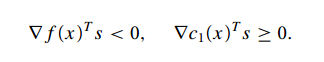
都是基于

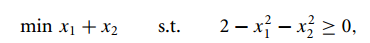
这样一个假设，不过我们一般假设的约束条件是小于等于0，所以看上去形式有点不一样，其实道理都一样的。